
- •Введение
- •Глава I. Основы линейной алгебры
- •1. Матрицы и действия над ними
- •2. Определители второго и третьего порядка. Обратная матрица
- •3. Системы линейных алгебраических уравнений
- •Формулы Крамера
- •3.2 Матричный способ решения системы линейных алгебраических уравнений
- •4. Метод Гаусса решения произвольных систем линейных алгебраических уравнений
- •5. Собственные числа и собственные векторы матрицы
- •Глава 2. Элементы векторной алгебры и аналитической геометрии. Комплексные числа
- •1. Элементы векторной алгебры и аналитической геометрии в пространстве
- •2. Аналитическая геометрия на плоскости
- •3. Линии второго порядка
- •4. Полярная система координат
- •5. Комплексные числа
- •Глава 3. Введение в анализ. Дифференциальное исчисление функции одной переменной.
- •1. Предел функции
- •2. Непрерывность функции
- •3. Дифференцирование функций
- •5. Исследование функций
- •Задачи для контрольных работ Контрольная работа №1 Основы линейной алгебры
- •Контрольная работа №2 Элементы векторной алгебры и аналитической геометрии. Комплексные числа
- •Контрольная работа № 3 Введение в анализ. Дифференциальное исчисление функции одной переменной
2. Непрерывность функции
Функция называется непрерывной в точке , если:
1) эта функция определена в некоторой окрестности точки
2) 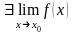
3) 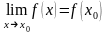 .
.
Теорема.
Для того чтобы функция
была непрерывна в точке
,
необходимо и достаточно, чтобы выполнялись
равенства:
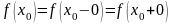 .
.
Точка называется точкой разрыва непрерывности функции, если в этой точке функция не является непрерывной, т.е. если в этой точке нарушается хотя бы одно из условий определения непрерывности функции.
Если
существуют конечные односторонние
пределы
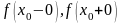 ,
причем не все три числа
,
причем не все три числа
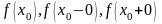 равны между собой, то
называется точкой
разрыва
первого
рода.
В частности, если:
равны между собой, то
называется точкой
разрыва
первого
рода.
В частности, если:
1)
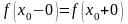 ,
то
называется устранимой
точкой разрыва;
,
то
называется устранимой
точкой разрыва;
2)
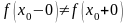 ,
то
называется точкой
разрыва типа скачка,
причем разность
,
то
называется точкой
разрыва типа скачка,
причем разность
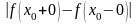 называется скачком
функции
в точке
.
называется скачком
функции
в точке
.
Точки разрыва функции, не являющиеся точками разрыва первого рода, называются точками разрыва второго рода.
Справедливо следующее утверждение.
Задание
2.
Задана функция
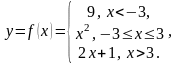
Исследовать функцию на непрерывность. Сделать чертеж.
Решение
Функция
задана различными непрерывными
аналитическими выражениями для различных
областей изменения аргумента
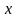 .
Следовательно, точками разрыва данной
функции могут быть только те точки, в
которых меняются аналитические выражения
функции, т.е. точки
.
Следовательно, точками разрыва данной
функции могут быть только те точки, в
которых меняются аналитические выражения
функции, т.е. точки
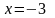 и
и
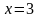 .
Определим значения функции и ее
односторонние пределы в этих точках:
.
Определим значения функции и ее
односторонние пределы в этих точках:
1) :
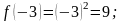
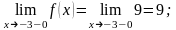
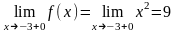 .
.
Так
как
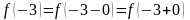 ,
то в точке
,
то в точке
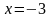 функция
непрерывна.
функция
непрерывна.
2) :
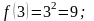
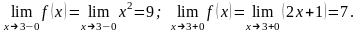
Так
как
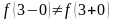 ,
то точка
является точкой разрыва непрерывности
функции
первого рода типа скачка.
,
то точка
является точкой разрыва непрерывности
функции
первого рода типа скачка.
Скачок
функции в точке разрыва равен:
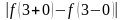 =2.
График функции
представлен на рисунке:
=2.
График функции
представлен на рисунке:
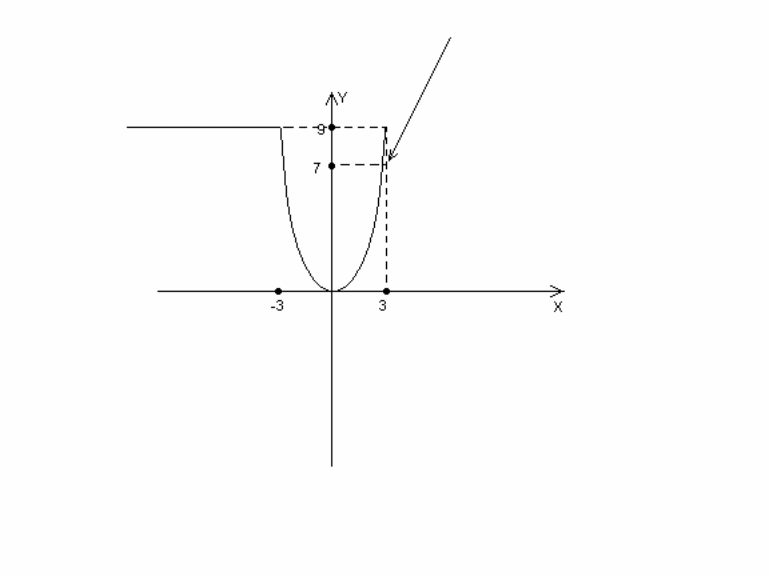
3. Дифференцирование функций
Производной
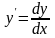 функции
в точке
называется предел отношения приращения
функции
функции
в точке
называется предел отношения приращения
функции
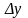 к приращению аргумента
к приращению аргумента
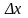 ,
при условии, что
стремится к нулю.
,
при условии, что
стремится к нулю.
То есть:
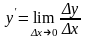 .
.
Основные правила нахождения производной
Если
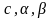 -
-
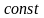 и
и
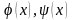 -
дифференцируемые функции в точке
,
(т.е. функции, имеющие производные в
точке
),
то:
-
дифференцируемые функции в точке
,
(т.е. функции, имеющие производные в
точке
),
то:
1)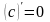 ;
;
2)
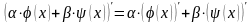 ;
;
3)
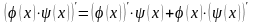
4)
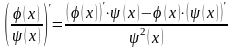 .
.
Таблица производных основных функций
1.
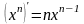 8.
8.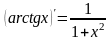
2.
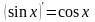 9.
9.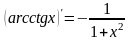
3.
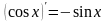 10.
10.
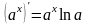
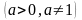
4.
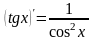 11.
11.
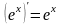
5.
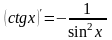 12.
12.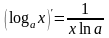
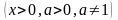
6.
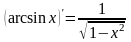
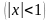 13.
13.
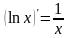
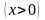
7.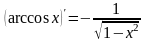
Правило
дифференцирования сложной функции.
Если
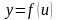 и
и
![]() ,
т.е.
,
т.е.
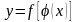 ,
где
,
где
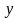 и
и
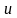 имеют производные, то
имеют производные, то
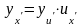 .
.
Дифференцирование
функции, заданной параметрически.
Пусть зависимость переменной
от переменной
задана параметрически посредством
параметра
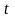 :
:
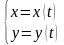 ,
,
Тогда
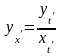 .
.
Задание 3. Найти производные данных функций.
1)
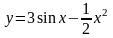
Решение. Применяя правило 2 нахождения производных и формулы 1 и 2 таблицы производных, получаем:
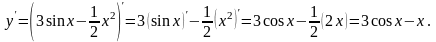
2)
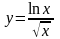
Решение. Применяя правило 4 нахождения производных и формулы 1 и 13 таблицы производных, получаем:
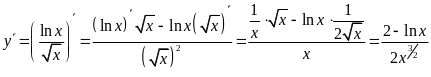 .
.
3)
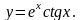
Решение. Применяя правило 3 нахождения производных и формулы 5 и 11 таблицы производных, получаем:
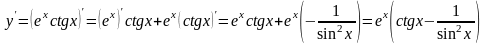 .
.
4)
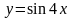
Решение.
Полагая
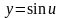 ,
где
,
где
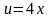 ,
согласно формуле нахождения производной
сложной функции, получим:
,
согласно формуле нахождения производной
сложной функции, получим:
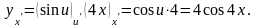
5)
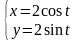
Решение.
Имеем:
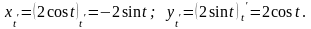 Тогда, согласно формуле нахождения
производной функции, заданной
параметрически, получаем:
Тогда, согласно формуле нахождения
производной функции, заданной
параметрически, получаем:
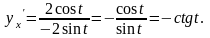
4. Производные высших порядков. Правило Лопиталя.
Производной
второго порядка функции
называется производная от ее производной,
т.е.
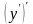 .
Для второй производной используются
следующие обозначения:
.
Для второй производной используются
следующие обозначения:
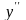 или
или
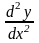 ,
или
,
или
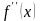 .
.
Производной
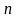 -
го порядка от функции
называется производная от ее производной
-
го порядка от функции
называется производная от ее производной
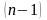 -го
порядка. Для производной
-го
порядка используются следующие
обозначения:
-го
порядка. Для производной
-го
порядка используются следующие
обозначения:
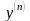 или
или
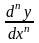 ,
или
,
или
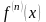 .
.
Правило
Лопиталя.
Пусть функции
и
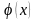 дифференцируемы в окрестности точки
,
причем производная
дифференцируемы в окрестности точки
,
причем производная
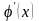 не обращается в нуль. Если функции
и
являются одновременно либо бесконечно
малыми, либо бесконечно большими при
,
и при этом существует предел отношения
не обращается в нуль. Если функции
и
являются одновременно либо бесконечно
малыми, либо бесконечно большими при
,
и при этом существует предел отношения
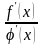 при
,
то существует также и предел отношения
при
,
то существует также и предел отношения
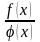 при
.
Причем
при
.
Причем
 .
.
Правило
применимо и в случае, когда
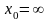 .
.
Заметим, что в некоторых случаях раскрытие неопределенностей вида или может потребовать неоднократного применения правила Лопиталя.
Неопределенности
вида
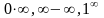 и т.д. с помощью элементарных преобразований
легко сводятся к неопределенностям
вида
или
.
и т.д. с помощью элементарных преобразований
легко сводятся к неопределенностям
вида
или
.
Задание
4.
Найти предел
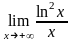 ,
пользуясь правилом Лопиталя.
,
пользуясь правилом Лопиталя.
Решение
Здесь мы имеем неопределенность вида
,
т.к.
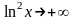 при
при
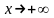 .
Применим правило Лопиталя:
.
Применим правило Лопиталя:
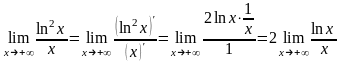 .
.
После
применения правила Лопиталя мы снова
получили неопределенность вида
,
т.к.
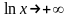 при
.
Применяя снова правило Лопиталя повторно,
получим:
при
.
Применяя снова правило Лопиталя повторно,
получим:
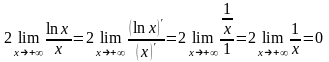 .
.
