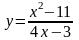- •Введение
- •Глава I. Основы линейной алгебры
- •1. Матрицы и действия над ними
- •2. Определители второго и третьего порядка. Обратная матрица
- •3. Системы линейных алгебраических уравнений
- •Формулы Крамера
- •3.2 Матричный способ решения системы линейных алгебраических уравнений
- •4. Метод Гаусса решения произвольных систем линейных алгебраических уравнений
- •5. Собственные числа и собственные векторы матрицы
- •Глава 2. Элементы векторной алгебры и аналитической геометрии. Комплексные числа
- •1. Элементы векторной алгебры и аналитической геометрии в пространстве
- •2. Аналитическая геометрия на плоскости
- •3. Линии второго порядка
- •4. Полярная система координат
- •5. Комплексные числа
- •Глава 3. Введение в анализ. Дифференциальное исчисление функции одной переменной.
- •1. Предел функции
- •2. Непрерывность функции
- •3. Дифференцирование функций
- •5. Исследование функций
- •Задачи для контрольных работ Контрольная работа №1 Основы линейной алгебры
- •Контрольная работа №2 Элементы векторной алгебры и аналитической геометрии. Комплексные числа
- •Контрольная работа № 3 Введение в анализ. Дифференциальное исчисление функции одной переменной
Контрольная работа № 3 Введение в анализ. Дифференциальное исчисление функции одной переменной
Задание 1. Найти пределы функций, не пользуясь правилом Лопиталя.
1.
а)
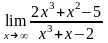 ;
б)
;
б)
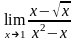 ;
в)
;
в)
 ;
г)
;
г)
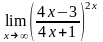
2.
а)
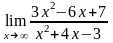 ;
б)
;
б)
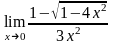 ;
в)
;
в)
 ;
г)
;
г)
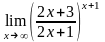
3.
а)
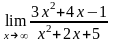 ;
б)
;
б)
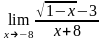 ;
в)
;
в)
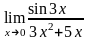 ;
г)
;
г)
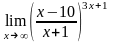
4.
а)
 ;
б)
;
б)
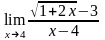 ;
в)
;
в)
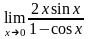 ;
г)
;
г)
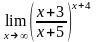
5.
а)
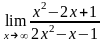 ;
б)
;
б)
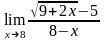 ;
в)
;
в)
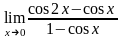 ;
г)
;
г)
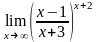
6.
а)
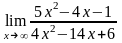 ;
б)
;
б)
 ;
в)
;
в)
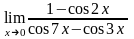 ;
;
г)

7.
а)
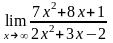 ;
б)
;
б)
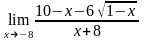 ;
в)
;
в)
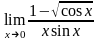 ;
г)
;
г)
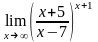
8.
а)
 ;
б)
;
б)
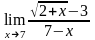 ;
в)
;
в)
 ;
г)
;
г)
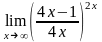
9.
а)
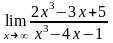 ;
б)
;
б)
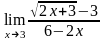 ;
в)
;
в)
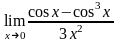 ;
г)
;
г)
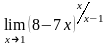
10.
а)
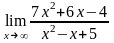 ;
б)
;
б)
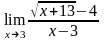 ;
в)
;
в)
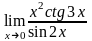 ;
г)
;
г)
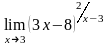 .
.
Задание 2. Исследовать на непрерывность данные функции. Сделать чертеж.
1.
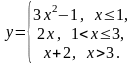 2.
2.
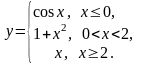
3.
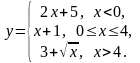 4.
4.
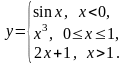
5.
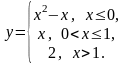 6.
6.
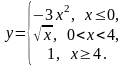
7.
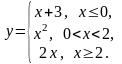 8.
8.
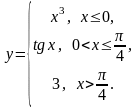
9.
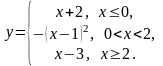 10.
10.

Задание 3. Найти производные данных функции.
1. а)
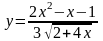 ;
б)
;
б)
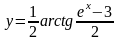 ;
в)
;
в)
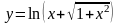 ;
;
г)
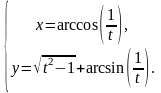
2. a)
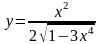 ;
б)
;
б)
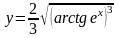 ;
в)
;
в)
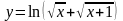 ;
;
г)
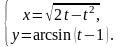
3. a)
 ;
б)
;
б)
 ;
в)
;
в)
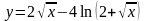 ;
г)
;
г)
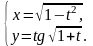
4. а)
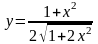 ;
б)
;
б)
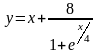 ;
в)
;
в)
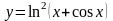 ;
г)
;
г)

5. а)
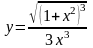 ;
б)
;
б)
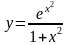 ;
в)
;
в)
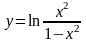 ;
г)
;
г)
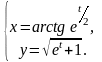
6. а)
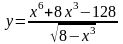 ;
б)
;
б)
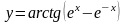 ;
в)
;
в)
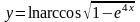 ;
;
г)
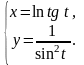
7. а)
 ;
б)
;
б)
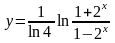 ;
в)
;
в)
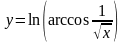 ;
г)
;
г)

8. а)
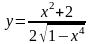 ;
б)
;
б)
 ;
в)
;
в)
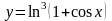 ;
;
г)
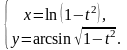
9. а)
 ;
б)
;
б)
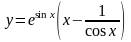 ;
в)
;
в)
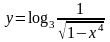 ;
г)
;
г)
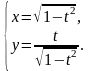
10. а)
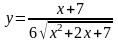 ;
б)
;
б)
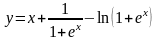 ;
в)
;
в)
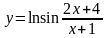 ;
;
г)
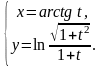
Задание 4. Найти пределы функций, пользуясь правилом Лопиталя.
1.
 2.
2.
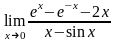
3.
 4.
4.
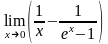 .
.
5.
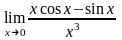 6.
6.
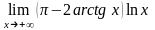
7.
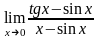 8.
8.
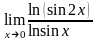
9.
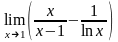 10.
10.
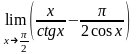
Задание 5. Провести полное исследование функций и построить их графики.
1.
 2.
2.
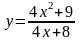
3.
 4.
4.
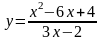
5.
 6.
6.
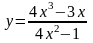
7.
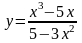 8.
8.
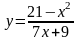
9.
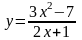 10.
10.