Розділ 2. ІНТЕРПОЛЮВАННЯ ФУНКЦІЙ.

ПОСТАНОВКА ЗАДАЧІ

Н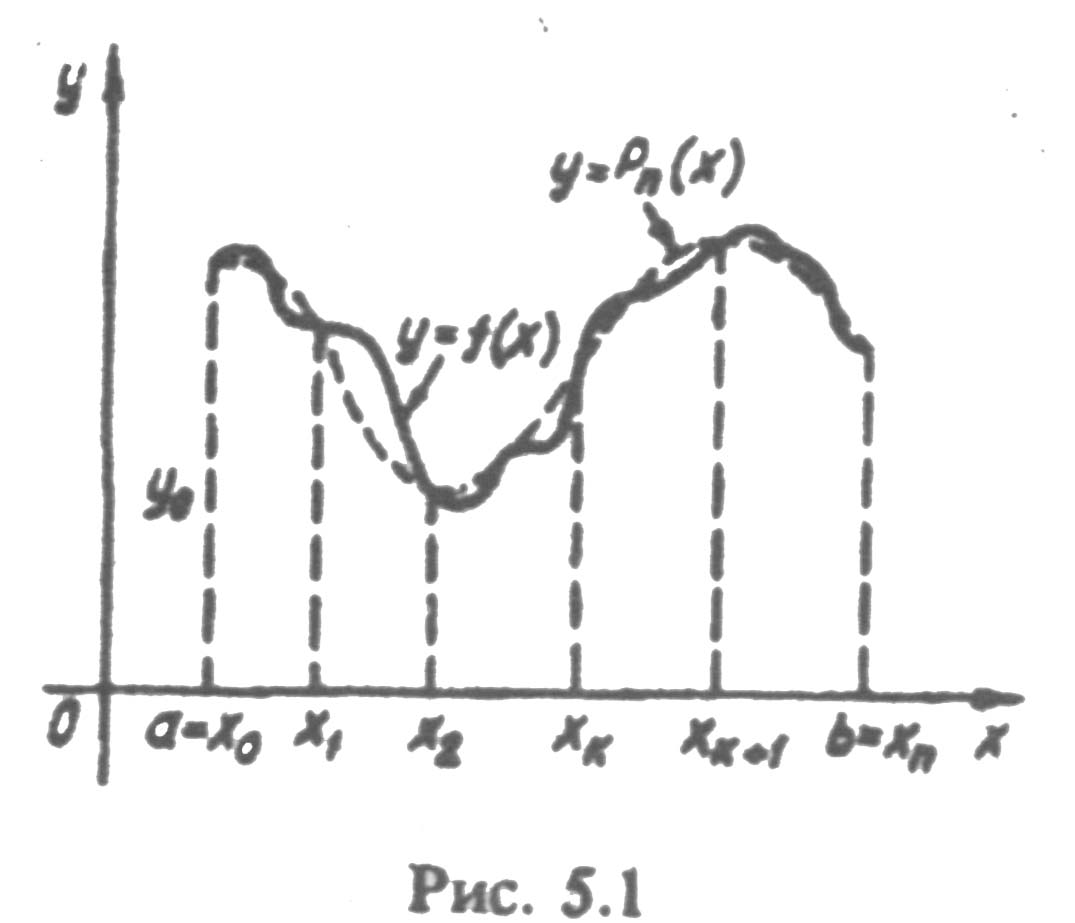 ехай на відрізку [а; b] визначено певний клас функцій {Р(x)}, наприклад клас алгебраїчних многочленів, а в точках x₀, x₁, ..., х_n цього проміжку задано значення деякої функції у₀ = f(х ₀), у₁ = f(x₁),• • • ,у_n = f(x_n). Наближену заміну функції f на відрізку [а; b] однією з функцій Р(х) цього класу так, щоб функція Р(х) в точках x₀, x₁, ..., х_n набувала тих самих значень, що й функція f, тобто щоб Р(х_і) =у_і (і =0, 1, ..., п), називають інтерполюванням, або інтерполяцією. Точки x₀, X₁, ..., Х_n називають вузлами інтерполювання, функцію Р(х)— інтерполюючою функцією, а формулу f(x)≈Р(х) за допомогою якої обчислюють значення функції f у проміжку [а; b], — інтерполяційною формулою.

З геометричного погляду задача інтерполювання полягає в знаходженні кривої у= Р(х) певного класу, яка проходить через точки площини з координатами (х_і, у_і) (і = 0, 1, ..., п) (рис. 2.1).

Якщо функція Р(х) належить класу алгебраїчних многочленів, то інтерполювання називається параболічним. Параболічне інтерполювання найзручніше, оскільки многочлени, які прості за формою і не мають особливих точок, можуть набувати довільних значень, їх легко обчислювати, диференціювати й інтегрувати.

У деяких випадках доцільніше використовувати інші класи інтерполюючих функцій. Якщо, наприклад, функція f періодична, то функцію Р(х) природно вибирати з класу тригонометричних многочленів, а якщо функція f перетворюється в нескінченність у заданих точках або поблизу них, то функцію Р(х) доцільно вибирати з класу раціональних функцій.

Розглядатимемо лише задачу параболічного інтерполювання, яку сформулюємо так: в n+1 різних точках X₀, X₁, ..., Х_n задано значення функції f:У₀ = f(Х ₀), У₁ = f(X₁), • • ,У_n = f(X_n) і треба побудувати многочлен

Pn (х) =q₀ xⁿ+ q₁х^n-1 + • • • + q_n, (2.1)

степеня n, який задовольняв би умови

f(x_i)=Pn(x_i), i=0,1, . . ., п (2.2)

Многочлен Рn(х), який задовольняє умови (2.2), називають інтерполяційним многочленом наближену рівність f(x)≈Рп(х) — інтерполяційною формулою, а різницю Rn(f,x)=f(x)- Рп(х) — залишковим членом інтерполяційної формули. Хоч інтерполяційний многочлен, що задовольняє умови (2.2), і єдиний, проте можливі різні форми його запису.

Інтерполяційний многочлен будують тоді, коли;

1) функцію задано таблично для деяких значень аргументу, а треба знайти її значення для значень аргументу, яких у таблиці немає;

2) функцію задано графічно, наприклад за допомогою самописного приладу, а треба знайти її наближений аналітичний вираз;

3) функцію задано аналітичне, але її вираз досить складний і незручний для виконання різних математичних операцій (диференціювання, інтегрування тощо).

Інтерполяційний многочлен лагранжа

Нехай у точках х_i (і = 0, 1, ..., п) , де Х₀ < X_i < ... < Х_п задано значення функції f : У₀ = f(Х ₀), У₁ = f(X₁), • • ,У_n = f(X_n) . Треба побудувати многочлен Ln(x) степеня n , який у вузлах хі (і=0,1,..., п) набуває тих самих значень, що й функція f, тобто

Ln(xi)=y_i, i= 0, 1, 2,. ..,n. (2.3)

Шукатимемо інтерполяційний многочлен Pn(x)будем за допомогою многочлена L_n у такому вигляді:

L_n (x,x _i ) = (Х—Х_о)(Х—Х₁) ••• (X—X_i-1)(X—X_i+1) ••• (Х—Х_п)

(X_i – X₀) (X_i – X₁) •••(X_i- X _i-1) (X_i-x_i+1)••(X_i-Хn) (2.4)

де

. (2.5)

Тоді вираз інтерполяційного многочлена Р_п (х) має

Р_п (х) =  L_n(Х, Xi)* Yi = L_n (х, х_о) у ₀ + L_n (х, x₁)y₁+• • • + L_n (х, x_n)y_n=

(2.6)

де многочлен степеня п, відповідає, умовам (2.5) і умовам (2.3).

Многочлен Pn(x) виду (2.6) називають інтерполяційним многочленом Лагранжа, а наближену рівність f(x) ≈Рп(х) — інтерполяційною формулою Лагранжа.

L_n(Х, Xi) (і =0, 1, ..., п) у многочлені Лагранжа називають коефіцієнтами Лагранжа.

Розглянемо два окремих випадки інтерполяційної формули Лагранжа (2.6).

1. Нехай n=1, тобто значення функції f задано в двох вузлах х_о і х₁. Позначимо ці значення у_о і у₁. Тоді з формули (5.6) дістанемо

Р₁ (х) = Ln (х, х_о) у ₀ + Ln (х, x₁)y₁₌ (2.7)

Формулу (2.7) називають формулою лінійного інтерполювання. При лінійному інтерполюванні дуга кривої у=f(x) на відрізку [x_о; х₁] замінюється відрізком прямої (2.7), що лежить між точками (x_о;у_о) і (х₁; у₁).

2. Нехай n=2. Функцію f задано в трьох вузлах х_і (і = 0, 1,2) значеннями уі (і =0, 1, 2). У цьому разі формула (5.6) набирає вигляду

P₂ (x) = L₂ (x, x₀) У₀ + L₂ (x, x₁) У₁ + L, (x, x₂) У₂ (2.8)

Формулу (5.11) називають формулою квадратичного інтерполювання. При квадратичному інтерполюванні дуга кривої у =f(x) на відрізку [x_о; х₂] замінюється дугою параболи, що проходить через точки (хі; уі) ,i=0, 1, 2.

Оцінка похибки інтерполяційної формули Лагранжа, Якщо функція f на відрізку [a; b] є многочленом степеня, що менший або дорівнює n, то з єдиності інтерполяційного многочлена випливає, що інтерполяційний многочлен Ln(x) тотожно дорівнює f, тобто f(x)-Pn(x) ≡ О, х є [а; b].

Якщо f на відрізку [а; b], який містить вузли інтерполяції хі (і =0, 1,...,n), не є многочленом степеня, що менший або дорівнює n, то різниця

Rn(f,x) =f(x)-Pn(x) -(2.9)

дорівнюватиме нулю лише у вузлах інтерполяції хі (і =0, 1, ..., n), а в інших точках відрізка [а; b] вона відмінна від тотожного нуля. Функцію Rn(f,x), яка характеризує точність наближення функції f інтерполяційним многочленом Pn(x) , називають залишковим членом інтерполяційної формули Лагранжа (2.6), або похибкою інтерполювання. Якщо відомий аналітичний вираз функції f , то можна оцінити Rn(f,x).

Справедлива така теорема.

Теорема. Якщо вузли інтерполювання хі (і =0, 1, …, n) різні і належать відрізку [а; b] , а функція f диференційована n+1 раз на відрізку [а; b], то для будь-якої точки х Є [а; b] існує така точка хє [а; b], що для похибки інтерполювання справедлива рівність

Rn (х)  M_n+1

(2.10)

де M_n+1=max f⁽ⁿ⁺¹⁾(x).

З формули (2.10) видно, що абсолютна похибка інтерполяційної формули Лагранжа пропорційна добутку двох множників M_n+1 і │(x-x₀)(x-x₁)…(x-x_n)│, з яких M_n+1 залежить лише від функції f , а величина другого│(x-x₀)(x-x₁)…(x-x_n) │, визначається виключно вибором вузлів інтерполювання. Зменшити величину абсолютної похибки інтерполяційної формули Лагранжа можна таким вибором вузлів інтерполювання, за якого множник │(x-x₀)(x-x₁)…(x-x_n) │ набуває найменшого максимального значення на відрізку [а;b].

Приклад 1. Побудувати інтерполяційний многочлен Лагранжа для функції f(x)=lnх з вузлами x=2,3,4 і оцінити погрішність інтерполяційного многочлена при х=2,5. Значення функції у вузлах інтерполяції

х	2,	3	4
F(x)	0,6931	1,0986	1,3863

Многочлен Лагранжа будемо будувати по наступній формулі:

Р_п (х) =  L_n(Х, Xi)* Yi = L_n (х, х_о) у ₀ + L_n (х, x₁)y₁+• • • + L_n (х, x_n)y_n=

Тут п =2 і

Р₂(х)=0.6931 +1,0986 +1,3863 =-0,4713+0,7000x- 0,0589x².

Для оцінки погрішності скористаємося нерівністю

|R ₂ (2,5)|<М₃(2; 4)-

де |A₃(2,5)| =0,5*0,5*1,5 =0,375,

f(x)=lnx, f’(x)=1/x, f’’(x)=-1/x², f’’’(x)=2/x³

Звідси відповідно M₃ (2; 4) = 1/4 , і остаточно

|R ₂ (2,5)|<0,25 =0,0156.

Насправді погрішність менше. Визначаючи ln2,5 чотиризначним таблицям, знайдемо

ln2,5-Р₂ (2,5) =0,9163—0,9103=0,0057.

Інтерполяційний многочлен Лагранжа може бути побудований при будь-якім розташуванні вузлів інтерполяції. Однако, якщо буде потрібно для поліпшення наближення підвищити на одиницю число вузлів (тобто степеня многочлена) додатком нового вузла, многочлен Лагранжа прийдеться переобчислити заново. У цьому відношенні значно користатися інтерполяційним многочлен Ньютона, до побудови якого ми і переходимо.