
- •Раздел первый с татика
- •Глава I
- •§ 1. Механическое движение. Равновесие
- •§ 2. Материальная точка. Абсолютно твёрдые и деформируемые тела
- •§ 3. Сила – вектор. Система сил. Эквивалентность сил
- •§ 4. Основные аксиомы статики
- •§ 5. Связи и их реакции
- •Глава II плоская система сходящихся сил
- •§ 6. Геометрический метод сложения сил, приложенных
- •В одной точке
- •§ 7. Проекция силы на ось
- •§ 8. Проекция векторной суммы на ось
- •§ 9. Аналитическое определение величины и направления равнодействующей плоской системы сходящихся сил (метод проекций)
- •§ 10. Уравнения равновесия плоской системы сходящихся сил
- •§ 11. Решение задач на равновесие плоской системы сходящихся сил
- •Глава III Пара сил и моменты сил
- •§ 12. Пара сил и ее действие на тело
- •§ 13. Эквивалентность пар
- •§ 14. Сложение пар
- •§ 15. Момент силы относительно точки и оси
- •Глава IV Система произвольно расположенных сил
- •§ 16. Приведение силы к точке
- •§ 17. Приведение плоской системы сил к данной точке
- •§ 18. Теорема о моменте равнодействующей (теорема Вариньона)
- •§ 19. Уравнение равновесия плоской системы сил
- •§ 20. Опорные устройства балочных систем
- •§ 21. Решение задач на равновесие плоской системы сил
- •§ 22. Пространственная система сил
- •Глава V Центр тяжести. Геометрические характеристики плоских сечений
- •§ 23. Центр параллельных сил и его координаты
- •§ 24 Центры тяжести площадей. Статические моменты площадей
Глава II плоская система сходящихся сил
§ 6. Геометрический метод сложения сил, приложенных
В одной точке
Силы называют сходящимися, если их линии действия пересекаются в одной точке.
Различают плоскую систему сходящихся сил, когда линия действия всех данных сил лежит в одной плоскости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных плоскостях.
На основании следствия из третьей аксиомы, силу можно переносить по линии её действия, поэтому сходящиеся силы всегда можно перенести в одну точку – в точку пересечения их линий действия.
Рассмотрим плоскую систему сходящихся сил. На рис. 6, а приведена такая система сил, линии действия которых пересекаются в точке К. Пользуясь указанным следствием из третьей аксиомы, перенесём все силы в точку К. Выполнив перенос, получим четыре силы P1, P2, P3 и P4, приложенные к точке К. Для определения их равнодействующей сложим последовательно все данные силы, используя правило треугольника (рис. 6, б). Сложим сначала две силы P1 и P2. Из произвольной точки О проведём, сохраняя масштаб и направление, силу P1. Из конца силы P1 проведём вторую силу P2. Соединив точку О с концом силы P1, получим силы R1, равную сумме сил P1и P2, R1 = P1 + P2.
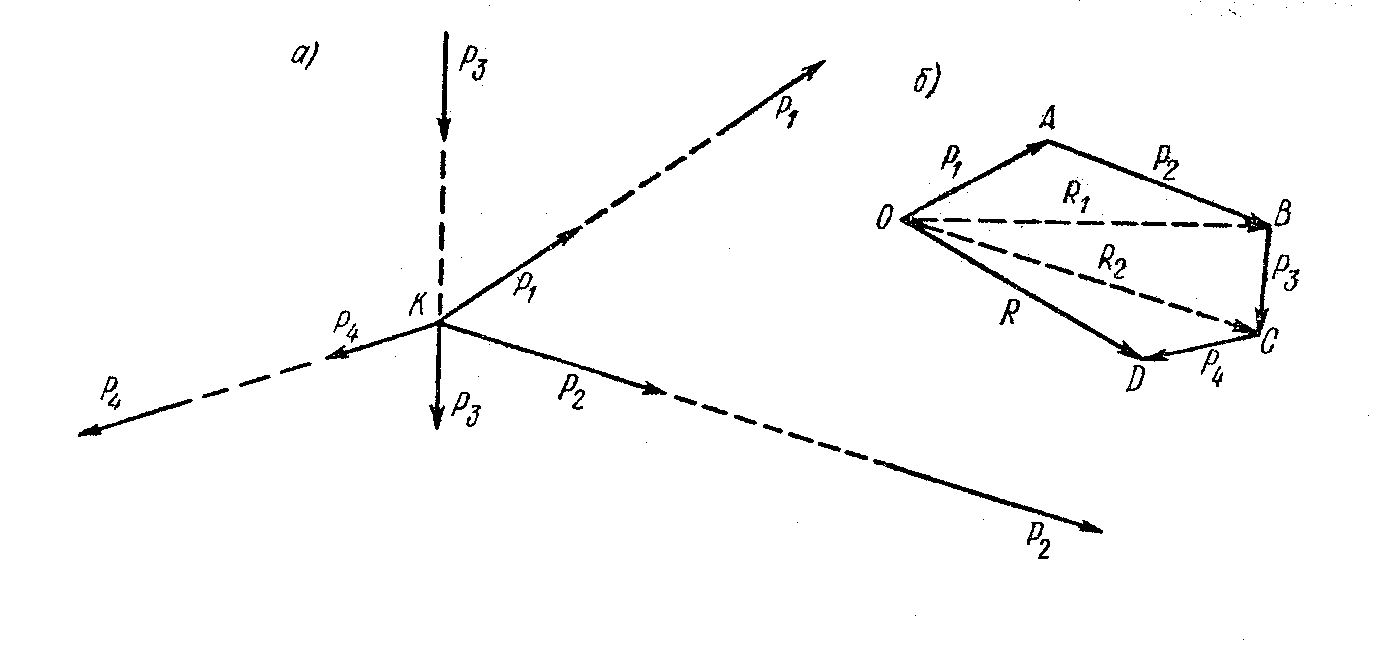
Рис. 6
Из конца силы R1 проведём третью силу P3. Соединив точку О с концом силы P3, получим силу R2, равную сумме сил P3 и R1, т. е. R2 = P3 + R1, но R1 = P1 + P2. Следовательно,
![]() =
+
=
+
![]() +
+
![]() .
.
Из конца силы
проведём четвёртую, последнюю
силу
![]() .
Соединив точку O с
концом вектора силы
,
получим силу
.
Соединив точку O с
концом вектора силы
,
получим силу
![]() ,
равную сумме сил
и
,
т.е.
,
равную сумме сил
и
,
т.е.
=
+
=
+
+
+
=
![]() .
(3)
.
(3)
Промежуточные векторы
![]() и
можно не строить, а последовательно, в
указанном выше порядке одну за другой
отложить все заданные силы и начало
первой соединить с концом последней.
и
можно не строить, а последовательно, в
указанном выше порядке одну за другой
отложить все заданные силы и начало
первой соединить с концом последней.
Фигура OABCD (см. рис. 6, б) называется силовым многоугольником. Замыкающая сторона этого многоугольника представляет собой равнодействующую заданной системы сил, равную их геометрической сумме. Необходимо обратить внимание на то, что равнодействующая сила всегда направлена от начала первого слагаемого к концу последнего слагаемого. Иными словами, стрелка равнодействующей силы всегда направлена навстречу обходу многоугольника, соответствующему последовательному сложению заданных сил (см. рис. 6, б).
Когда при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодействующая системы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил будет находиться в равновесии.
Самозамыкание силового многоугольника данной системы сходящихся сил является геометрическим условием её равновесия. Таким образом, для уравновешенной системы сходящихся сил вектор равнодействующей обращается в точку.
§ 7. Проекция силы на ось
Построение силовых многоугольников требует сложных и громоздких построений и не даёт достаточно точных результатов. В таких случаях прибегают к другому методу, где геометрическое построение заменено вычислениями скалярных величин. Это достигается проектированием заданных сил на оси прямоугольной системы координат.
Осью называют прямую линию, которой приписано определённое направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на неё из начала и конца вектора.
Проекция вектора считается положительной (+), если направление от начала проекции к её концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (−), если направление от начала проекции к её концу противоположно положительному направлению оси.
Рассмотрим ряд случаев проектирования сил на ось.
1. Дана сила (рис. 7, а), она лежит в одной плоскости с осью x. Вектор силы составляет с положительным направлением оси острый угол α. Чтобы найти величину проекции, из начала и конца вектора силы опускаем перпендикуляры на ось x; получаем
Px = ab = P cos α. (4)
Проекция вектора в данном случае положительна.
2. Дана сила (рис. 7, б), которая лежит в одной плоскости с осью x, но её вектор составляет с положительным направлением оси тупой угол α. Проекция силы Q на ось x отрицательна
Qx = - ab = - Q cos α. (5)
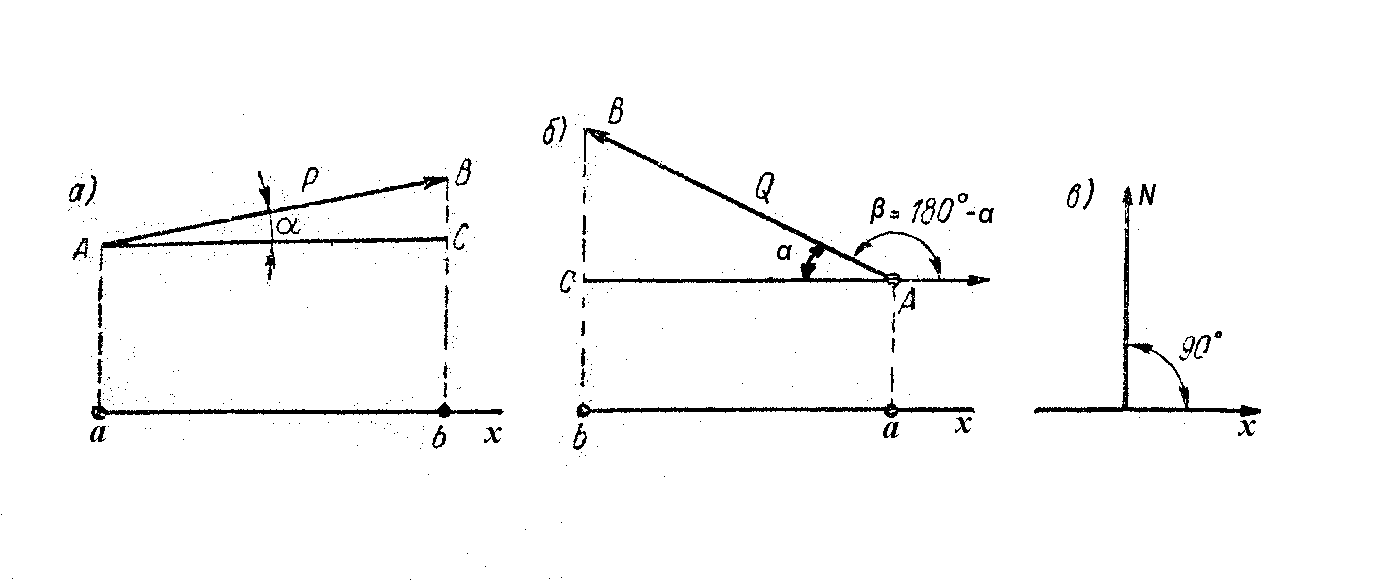
Рис. 7
3. Дана сила
![]() ,
перпендикулярная оси x
(рис. 7, в). Проекция силы
на ось x равна нулю,
т.е. Nx
= N cos
90° = 0.
,
перпендикулярная оси x
(рис. 7, в). Проекция силы
на ось x равна нулю,
т.е. Nx
= N cos
90° = 0.
Итак, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.
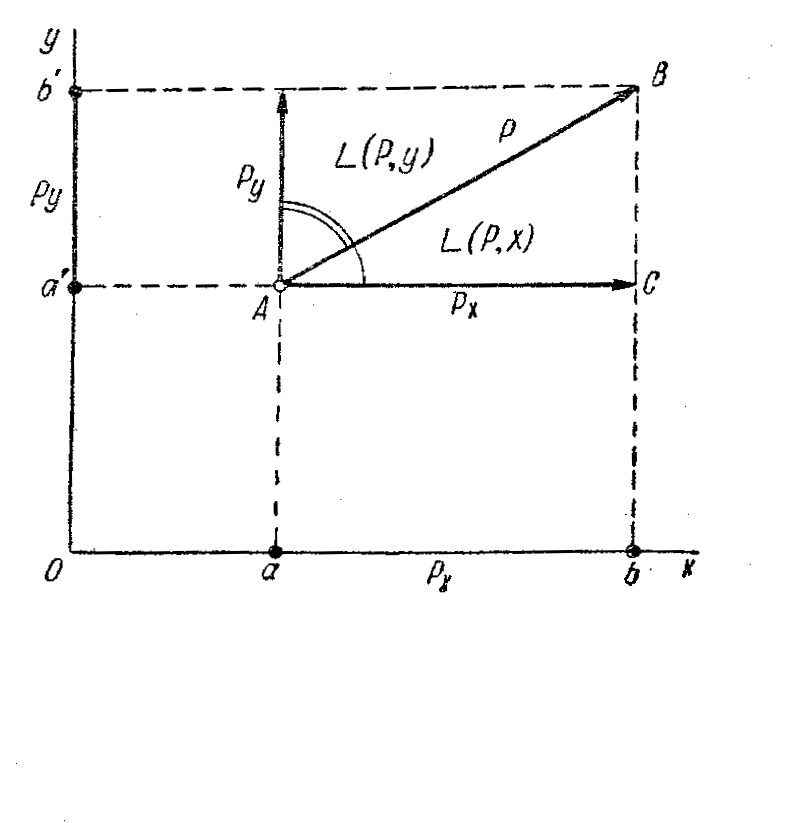
Рис. 8
Силу, расположенную на плоскости xOy (рис. 8), можно спроектировать на две координатные оси Ox и Oy. На рисунке изображена сила и её проекции Px и Py. Ввиду того, что проекции образуют между собой прямой угол, из прямоугольного треугольника ABC следует:
![]() (6)
(6)
Этими формулами можно пользоваться для определения величины и направления силы, когда известны её проекции на координатные оси.
