Глава IV Система произвольно расположенных сил

§ 16. Приведение силы к точке

Рассмотрим случай переноса силы в произвольную точку, не лежащую на линии действия силы (рис. 18, а).

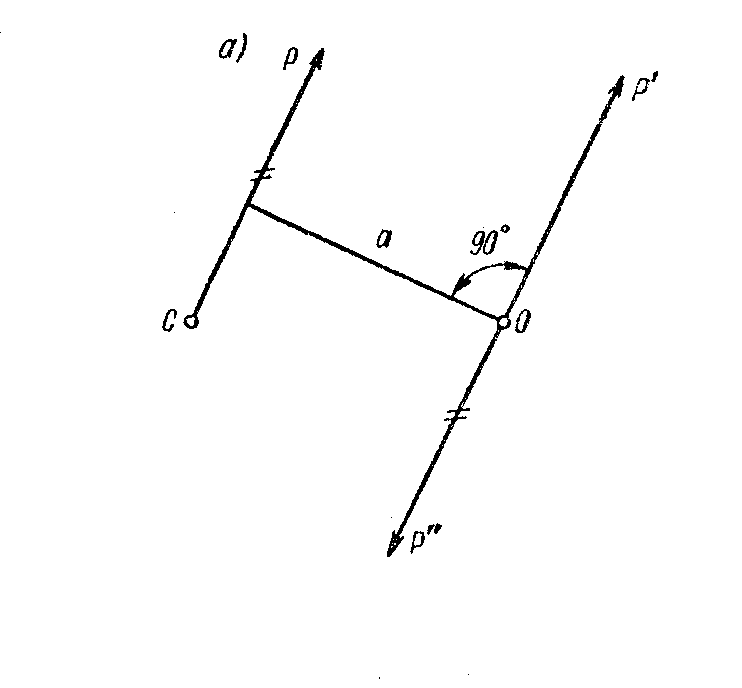
Рис. 18

Возьмем силу , приложенную в точке С. Требуется перенести эту силу параллельно самой себе в некоторую точку О. Приложим в точке О две силы ^’ и ^’’, противоположно направленные, равные по модулю и параллельные заданной силе ,т.е. P^’= P^’’=P. От приложения в точке О этих сил состояние тела не изменяется, так как они взаимно уравновешиваются. Опустим из точки О на линию действия силы перпендикуляр а, тогда полученную систему трех сил можно рассматривать как состоящую из силы ^’, приложенной в точке О, и пары сил " с моментом М =- Ра. Эту пару сил называют присоединенной.

Таким образом, при приведении силы к точке, не лежащей на линии действия силы, получается эквивалентная система, состоящая из силы, такой же по модулю и направлению, как и сила , и присоединенной пары сил, момент которой равен моменту данной силы относительно точки приведения:

M_o ( ) = -Pa.

§ 17. Приведение плоской системы сил к данной точке

Описанный метод приведения одной силы к данной точке можно применить к какому угодно числу сил. Допустим, что в точках тела A,B,C и D (рис. 19) приложены силы ₁, ₂, ₃ и ₄ . Требуется привести эти силы к точке О плоскости. Приведем сначала силу ₁, приложенную в точке А. Приложим в точке О две силы ^’₁ и ^’’₁ , равные порознь по модулю заданной силе ₁ , параллельные ей и направленные в противоположные стороны. В результате приведения силы ₁ получим силу ^’₁ , приложенную в точке О, и пару сил ₁ ^’’₁ ( силы, образующие пару, отмечены черточками ) с плечом а₁. Поступив таким же образом с силой ₂ ,приложенной в точке В, получим силу ₂ , приложенную в точке О, и пару сил ₂ ^’’₂ с плечом а₂ и т.д.

Плоскую систему сил, приложенных в точках А, В, С и D, мы заменили сходящимися силами ^’₁ , ^’₂ , ^’₃ и ^’₄ , приложенными в точке О, и парами сил с моментами, равными моментам заданных сил относительно точки О:

М₁ = Р₁ а₁ =М_о( ₁); М₂ = ­ Р₂а₂ = М_о( ₂);

М₃ = – Р₃а₃ = М_о( ₃); М₄ = – Р₄а₄ = М_о( ₄).

Сходящиеся в точке силы можно заменить одной силой ^', равной геометрической сумме составляющих,

^' = ^'₁+ ^'₂+ ^'₃+ ^'₄ = ₁+ ₂+ ₃+ ₄ = _i . (16)

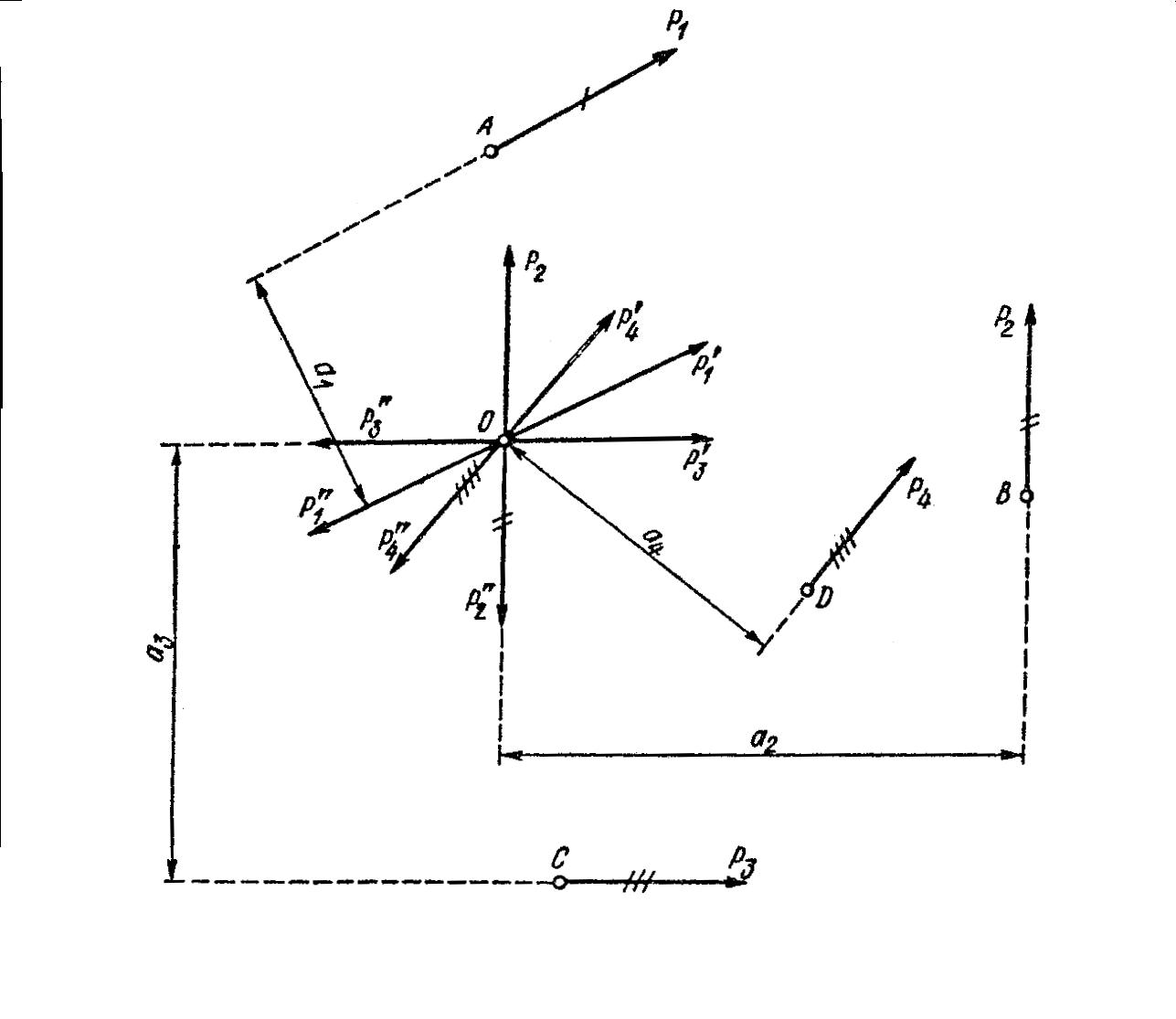
Рис. 19

Эту силу, равную геометрической сумме заданных сил, называют главным вектором системы сил.

На основании правила сложения пар сил из можно заменить результирующей парой, момент которой равен алгебраической сумме моментов заданных сил относительно точки О:

М_о = М₁ + М₂ + М₃ + М₄ = _i = _o( _i). (17)

По аналогии с главным вектором момент М₀ пары, равный алгебраической сумме моментов всех сил относительно центра приведения О, называют главным моментом системы относительно данного центра приведения О. Следовательно, в общем случае плоская система сил в результате приведения к данной точке О заменяется эквивалентной ей системой, состоящей из одной силы – главного вектора – и одной пары, момент которой называют главным моментом заданной системы сил относительно центра приведения.

Необходимо усвоить, что главный вектор ’ не является равнодействующей данной системы сил, так как эта система не эквивалентна одной силе ’. Только в частном случае, когда главный момент обращается в нуль, главный вектор будет равнодействующей данной системы сил. Так как главный вектор равен геометрической сумме сил данной системы, то ни модуль, ни направление его не зависят от выбора центра приведения. Величина и знак главного момента М₀ зависят от положения центра приведения, так как плечи составляющих пар зависят от взаимного положения сил и точки (центра), относительно которой берутся моменты.

Могут встретиться следующие случаи приведения системы сил:

1. ^'≠ 0; М_о ≠ 0 — общий случай; система приводится к главному вектору и к главному моменту.

2. ^'≠ 0; М_о = 0; система приводится к одной равнодействующей, равной главному вектору системы.

3. ^'= 0; М_о ≠ 0; система приводится к паре сил, момент которой равен главному моменту.

4. ^'= 0; М_о = 0; система находится в равновесии.

Можно доказать, что в общем случае, когда ^'≠ 0 и М_о ≠ 0, всегда есть точка, относительно которой главный момент системы сил равен нулю.

Рассмотрим плоскую систему сил, которая приведена к точке О, т.е. заменена главным вектором ^'≠ 0, приложенным в точке О, и главным моментом М_о ≠ 0 (рис. 20).

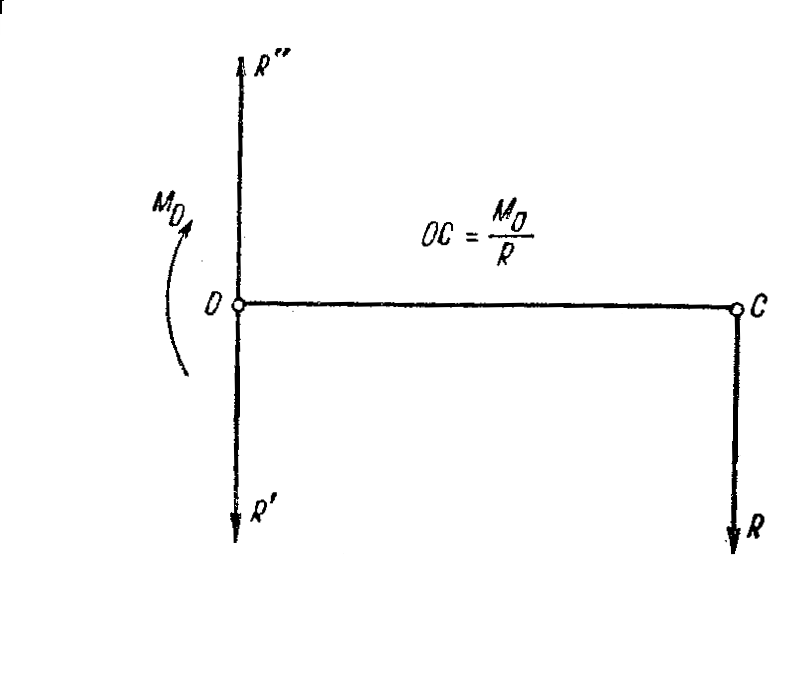
Рис. 20

Для определенности примем, что главный момент направлен по часовой стрелке, т.е. М_о < 0. Изобразим этот главный момент парой сил ^'', модуль которых выберем равным модулю главного вектора ^', т.е. R = R^’’= R^’. Одну из сил, составляющих пару, – силу ^'' – приложим в центре приведения О, другую силу – – в некоторой точке С, положение которой определится из условия: М_о = ОС*R. Следовательно,

ОС = . (18)

Расположим пару сил ^''так, чтобы сила ^''была направлена в сторону, противоположную главному вектору ^'. В точке О (рис. 20) имеем две равные взаимно противоположные силы ^' и ^'', направленные по одной прямой; их можно отбросить (согласно третьей аксиоме). Следовательно, относительно точки С главный момент рассматриваемой системы сил равен нулю, и система приводится к равнодействующей .