Основные статистические методы

После того как данные записаны в виде ряда характеризующих переменные значений, например, таких, как рост или частота сокращений сердца, полезно подсчитать их среднее значение и разброс значений. Оценки среднего значения называются характеристиками расположения относительно центра. Они включают среднее, медиану и моду. Оценки разброса величин называются мерой рассеяния, они включают дисперсию и стандартное отклонение.

Характеристики расположения относительно центра

Среднее (среднее арифметическое)

Это «средняя величина» группы значений, которую получают путем сложения всех значений и деления суммы на число сложенных значений.

Например, среднее для значений x₁, х₂, х.₃, x₄ ... х_n подсчитывается следующим образом:

или

где Σ - сумма или общее количество, х - отдельное значение и n - число отдельных значений.

Если одно и то же значение х встречается более чем один раз, среднее можно подсчитать, используя выражение:

где Σf - сумма частоты встречаемости х, или проще - n.

Медиана

Она представляет собой среднее, или центральное, значение группы переменных. Например, если пять значений х расположены в следующей последовательности: x₁, x₂, х₃, х₄ и х₅, то значение медианы будет равно х₃, так как равное число значений расположено до и после х₃. Если число значений четное, например от х₁ до х₆, то медиана будет равняться среднему из двух срединных значений:

.

Мода

Это значение переменной, встречающееся наиболее часто. Например, если число детей в десяти семьях соответственно равно 1, 1, 1, 2, 2, 2, 2, 3, 4, то мода равна 2.

Каждое из трех значений, описанных выше, имеет свои преимущества и недостатки и применяется при решении определенных задач. Проиллюстрировать применение среднего или моды можно на примере с различным числом детей в семьях. Среднее число детей в семье составляет 2,4, но так как ребенок - величина дискретная, естественно описывать число детей в семье в целых числах, т.е. с помощью моды, которая равна 2.

В случае нормального распределения значения среднего, медианы и моды совпадают (рис. 15, А). В случае того или иного уклона частоты распределения их значений не совпадают (рис. 15, Б).

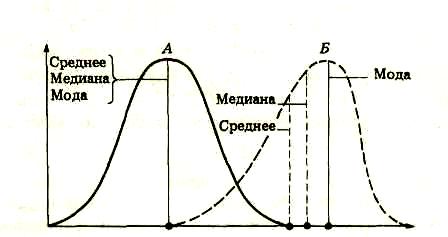
Рис. 15. Положение среднего, медианы и моды при нормальном распределении (А) и при распределении с уклоном (Б).

Оценки дисперсии

Для того чтобы оценить, в какой мере значения признака отклоняются от среднего, вычисляют среднее и дисперсию. Для нормального распределения это проиллюстрировано двумя кривыми на рис. 16. При статистическом анализе данных очень информативной является оценка среднего квадратичного или стандартного отклонения; по этим показателям можно предсказать и распределение значений вокруг среднего, и ответить на вопрос, достоверна ли разница между двумя группами данных.

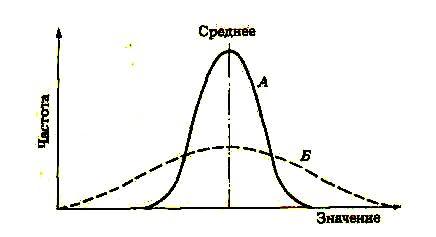
Рис. 16. Две кривые нормального распределения, демонстрирующие распределение двух совокупностей данных (возможно, характеризующих популяцию) с одинаковой общей частотой (т. е. площади под кривыми равны).

Кривая А построена по ограниченному ряду значений, сгруппированных вокруг среднего.

Кривая Б построена по широкому ряду значений, не сгруппированных вокруг среднего.

Стандартное отклонение

Стандартное отклонение (s) совокупности данных служит мерой отличия этих данных от среднего арифметического. Для его подсчета используют выражение:

где Σ - сумма, f - частота, х - отдельные значения и - среднее. Например, в выборке из десяти раковин блюдечка (Patella vulgaris), отобранных на скалистом берегу, эти раковины имеют следующие максимальные значения диаметров в миллиметрах: 36, 34, 41, 39, 37, 43, 36, 37, 41, 39. Чтобы определить среднее максимальное значение диаметра и стандартное отклонение, необходимо вычислить f, fx² и ², как это показано в следующей таблице:

х	f	fx	fх2
34	1	34	1156
36	2	72	2592
37	2	74	2738
39	2	78	3042
41	2	82	3362
43	1	43	1849
	Σf=10	Σ fx=383	Σ fх2=14739

Следовательно, = 38,3

² = 1466,9,

так как ,

следовательно, s = 2,65.

В этой популяции имеющих общее происхождение блюдечек среднее максимальное значение диаметра раковины равно 38,3 мм, а стандартное отклонение равно 2,7 мм (округлили до одной десятой). Если эти значения применить к более крупной популяции блюдечек общего происхождения, то на основе статистики можно предположить, что приблизительно 68% популяции будет иметь диаметр раковины 38,3 мм плюс-минус одно стандартное отклонение (2,7 мм), т. е. размеры раковин будут лежать в интервале от 35,6 до 41,0 мм; приблизительно 95% популяции будут иметь диаметр раковины 38,3 мм плюс-минус два стандартных отклонения (5,4 мм), т. е. диаметры будут лежать в интервале 32,9 - 43,7 мм, а практически 100% будут лежать в интервале плюс-минус три стандартных отклонения от 38,3 мм.

По величине стандартного отклонения можно судить о разбросе данных. Если стандартное отклонение мало, то, следовательно, разброс (отклонение от среднего) невелик и популяция в значительной степени однородна, как это показано на рис. 16, A. С увеличением стандартного отклонения увеличивается степень изменчивости внутри популяции, как показано на рис. 16, Б.

Дисперсия

Дисперсия - это квадрат стандартного отклонения. Дисперсия совокупности значений подсчитывается по следующей формуле:

Дисперсия

Где f - число значений в совокупности.

Дисперсию обычно подсчитывают в экологических исследованиях, включающих изучение питания, размножения и поведения, поскольку она служит показателем распределения организмов внутри популяции. Распределение может быть:

а) случайным;

б) групповым;

в) регулярным.

Для того чтобы определить тип распределения организмов внутри популяции, исследуемую площадь делят на квадраты равного размера и подсчитывают число организмов этой популяции в каждом квадрате. Исходя из этих данных, подсчитывают значение дисперсии по следующей формуле:

Среднее ; дисперсия ,

где f -число квадратов, содержащих х организмов. Используя выражение:

,

можно выделить три типа распределения (рис. 17).

Рис. 17. Типы распределения.

Связь между переменными

Данные всегда необходимо представлять таким образом, чтобы можно было выявить связи между двумя или более их совокупностями. Проще всего это сделать с помощью графика или диаграммы, показывающих связь между переменными. Но это целесообразно только в том случае, если одна из переменных (независимая переменная) находится под контролем экспериментатора, как, например, в случае, приведенном на рис. 8.

В других случаях, когда обе переменные являются независимыми, составляют таблицу, в которой значение одной помещают под соответствующим значением другой, как, например, в случае данных о росте и массе 20 студентов шестого курса, приведенных на рис. 18, A. На основе этих данных вычерчивают график (рис. 18, Б), который на­зывается диаграммой рассеяния. По внешнему виду графика видно, что эти две переменные связаны между собой некоторым образом, но эту связь невозможно описать более точно до тех пор, пока они не будут представлены в виде прямой линии, проходящей через точки графика.

Эта линия называется «линией наибольшего соответствия», или линией регрессии. Мера приближения точек к линии указывает на степень корреляции между двумя переменными. Линия наибольшего соответствия должна проходить через точку, соответствующую среднему значению массы и роста ( = 65,7 кг, = 165,8 см), а число точек над и под линией должно быть приблизительно одинаковым. По этой линии можно подсчитать рост, соответ­ствующий определенной массе.

А
Масса, кг	51	51	53	55	59	60	62	60	58	64	67	69	71	68	74	75	77	79	79	81
Рост, см	154	155	156	158	158	159	161	162	163	165	166	168	169	170	172	173	174	176	177	180

= 65,7 . = 165,8

Рис. 18. Данные о массе и соответствующем росте 20- и 16-летних студентов мужского пола представлены в виде таблицы (А) и диаграммы рассеяния (Б). Построена кривая регрессии.

Корреляция

Описанную выше связь между двумя переменными х и у можно обозначить термином корреляция. Между х и у могут существовать различные степени корреляции, как это показано на диаграммах рассеяния на рис. 19.

С помощью диаграммы рассеяния нельзя точно продемонстрировать значимость между совокупностями данных, так как этот способ субъективен. Значимость корреляции можно представить с помощью статистического критерия, называемого коэффициентом корреляции. Его величина может изменяться от - 1 до +1.

- 1 ― означает полностью отрицательную корреляцию, например отрицательную корреляцию между давлением кислорода в атмосфере и скоростью открывания дыхалец у насекомых;

0 ― означает отсутствие корреляции, например отсутствие корреляции между размерами плодов томатов и числом семян;

+ 1 ― означает полностью положительную корреляцию, например положительную корреляцию между возрастом и длиной тела у саранчи.

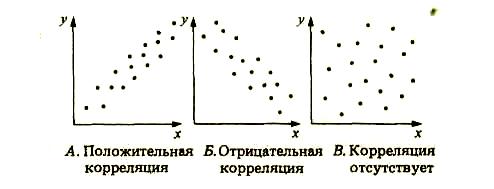
Рис. 19. Типы корреляции;

А - положительная корреляция; Б - отрицательная корреляция;

В-корреляция отсутствует.