
- •Глава 4.
- •Глава 6.
- •Глава 9.
- •Глава 10.
- •Глава 11.
- •Глава 12.
- •Глава 13.
- •Глава 14.
- •Глава 15.
- •Глава 16
- •Глава 18
- •Глава 1.
- •§ 1. Аксиомы и принципы статики твёрдого тела.
- •§ 2. Момент силы относительно произвольного центра, оси.
- •§ 3. Пара сил и её свойства.
- •§ 4.Главный вектор и главный момент системы сил. Правило Пуансо.
- •§ 5. Приведение системы сил к простейшему виду.
- •§ 6. Уравнения равновесия тела.
- •Глава 2. Центр параллельных сил и центр тяжести.
- •§ 1. Центр параллельных сил.
- •§ 2. Центр тяжести, методы определения координат центра тяжести.
- •Глава 3. Равновесие при наличии сил трения.
- •§ 1. Трение скольжения Угол трения, конус трения.
- •§ 2. Задача об опрокидывании тела. Трение качения.
- •Кинематика
- •Глава 4. Кинематика точки.
- •§ 1. Способы задания движения точки. Уравнения движения точки; траектория.
- •§ 2. Натуральный триэдр траектории.
- •§ 3. Скорость точки.
- •§ 4. Ускорение точки.
- •§ 5. Поступательное движение твердого тела.
- •Глава 5. Вращение твердого тела вокруг неподвижной оси.
- •§ 1 Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси.
- •§ 2. Векторные формулы скорости и ускорения точек тела, вращающегося вокруг неподвижной оси.
- •Глава 6. Кинематика плоского движения твердого тела
- •§ 1. Уравнения плоского движения.
- •§ 2. Скорости точек плоской фигуры.
- •§ 3. Мгновенный центр скоростей плоской фигуры.
- •§ 4. Ускорения точек плоской фигуры.
- •Глава 4. Вращение тела вокруг неподвижной точки. Общий случай движения тела.
- •§ 1. Определение положения твердого тела, имеющего неподвижную точку.
- •§ 2 Углы Эйлера, матрицы поворота.
- •§ 3. Угловая скорость и угловое ускорение твердого тела, имеющего неподвижную точку.
- •§ 4. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижного центра.
- •Глава 6.
- •§ 5. Определение положения твердого тела в пространстве.
- •§ 6. Скорости и ускорения в общем случае движения твердого тела.
- •Глава 8. .Кинематика относительного движения точки и тела.
- •§ 1. Абсолютное, относительное и переносное движения.
- •§ 2. Теорема о сложении скоростей в относительном движении.
- •§ 3. Сложение ускорений, теорема Кориолиса.
- •§ 4. Сложение вращений твёрдого тела.
- •§ 5. Общий случай движения тела (для скоростей).
- •Динамика точки и твёрдого тела
- •Глава 9. Динамика точки.
- •§ 1. Основные положения и аксиомы динамики
- •§ 2. Дифференциальные уравнения движения материальной точки.
- •§ 3. Динамики относительного движения точки.
- •Глава 10. Количество движения системы.
- •§ 1. Уравнения динамики системы материальных точек и твёрдого тела.
- •§ 2. Теорема об изменении количества движения системы материальных точек.
- •§ 3. Теорема о движении центра масс.
- •Глава 11. Кинетический момент системы и твёрдого тела.
- •§ 1. Теорема об изменении главного момента количества движения системы материальных точек.
- •§ 3. Кинетический момент тела, вращающегося относительно неподвижной точки.
- •§ 3. Момент инерции относительно произвольной оси. Тензор инерции.
- •§ 4. Главные оси инерции и главные моменты инерции.
- •§ 5. Вычисление моментов инерции.
- •§ 6. Преобразование моментов инерции.
- •§ 7. Кинетический момент твердого тела.
- •Глава 12. Дифференциальные уравнения движения твердого тела.
- •§ 1. Дифференциальные уравнения вращения твердого тела.
- •§ 2. Общий случай движения твердого тела.
- •§ 3. Динамика плоско-параллельного движения тела.
- •§ 4. Реакция оси вращающегося тела.
- •§ 5. Задача о физическом маятнике.
- •Глава 13. Кинетическая энергия системы и твёрдого тела.
- •§ 1. Кинетическая энергия системы материальных точек.
- •§ 2. Кинетическая энергия твердого тела.
- •§ 3. Работа силы. Мощность.
- •§ 4. Примеры вычисления потенциальной энергии и работы
- •§ 5. Теорема об изменении кинетической энергии.
- •§ 6. Закон сохранения механической энергии.
- •Динамика несвободной системы. __________________________________________________________Глава 14. Возможные перемещения.
- •§1. Связи, классификация связей, число степеней свободы.
- •§2. Возможные перемещения.
- •§ 3. Принцип освобождаемости. Идеальные связи.
- •§ 4. Статический принцип возможных перемещений.
- •§ 5. Динамический принцип возможных перемещений. Общее уравнение динамики.
- •Глава 15. Уравнение Лагранжа второго рода и его приложения.
- •§ 1. Вывод уравнения Лагранжа второго рода.
- •§ 2. Диссипативная функция.
- •§ 8. Представление кинетической энергии как функции обобщённых скоростей.
- •§ 9. Интеграл энергии.
- •Малые колебания системы с одной степенью свободы.
- •Глава 16 Свободные колебания системы с одной степенью свободы.
- •§ 1. Устойчивость равновесия голономной системы в консервативном силовом поле.
- •§ 2. Малые свободные колебания системы с одной степенью свободы.
- •§ 3. Свободные колебания системы с учётом линейно-вязкого сопротивления.
- •Глава 17.
- •§ 1. Вынужденные колебания без сопротивления. Биения, резонанс.
- •§ 2. Вынужденные колебания системы с учётом линейно-вязкого трения.
- •§ 3. Динамические характеристики вынужденных колебаний.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Глава 18 Уравнения статики деформируемого твёрдого тела.
- •§ 1. Дифференциальные уравнения равновесия нерастяжимой нити.
- •§ 2. Статика деформируемых прямых стержней.
- •Глава 19. Элементарная теория удара
- •§ 1. Теорема импульсов и её приложения в теории удара.
- •§ 2. Задача Герца о прямом и центральном ударе двух тел.
- •§ 3. Теоремы об изменении количества движения и кинетического момента при ударе.
- •§ 4. Удар, действующий на тело, вращающегося вокруг неподвижной оси.
- •§ 5. Условия отсутствия ударных реакций. Центр удара.
- •1.Статика.
- •2. Кинематика.
- •3. Динамика точки и твердого тела:
- •4. Динамика несвободной системы.
- •5. Колебания системы около положения устойчивого равновесия.
- •Дополнительные вопросы, включаемые по согласованию с выпускающими кафедрами: Динамические характеристики вынужденных колебаний. Нелинейные колебания точки. Метод Ван дер Поля.
- •3. Теорема о движении центра масс.
- •6. Теорема об изменении кинетической энергии.
§ 5. Поступательное движение твердого тела.
 Поступательное
движение и вращение вокруг неподвижной
оси являются наиболее простыми случаями
движения твердого тела. Движение твердого
тела называется поступательным, если
любая прямая, проведенная в теле, во
время движения остается параллельной
сама себе. Будем определять положение
любой точки А
твердого тела вектор-радиусом
Поступательное
движение и вращение вокруг неподвижной
оси являются наиболее простыми случаями
движения твердого тела. Движение твердого
тела называется поступательным, если
любая прямая, проведенная в теле, во
время движения остается параллельной
сама себе. Будем определять положение
любой точки А
твердого тела вектор-радиусом
![]() ,
проведенным из начала координат (рис.
24). Если движение поступательное, то по
определению вектор
,
проведенным из начала координат (рис.
24). Если движение поступательное, то по
определению вектор
![]() остается параллельным себе. Величина
вектора
не
изменяется, так как тело твердое. Итак,
является
постоянным вектором. Обозначим через
вектор-радиус
точки А,
а через
остается параллельным себе. Величина
вектора
не
изменяется, так как тело твердое. Итак,
является
постоянным вектором. Обозначим через
вектор-радиус
точки А,
а через
![]() -
вектор-радиус точки В,
относительно некоторой неподвижной
точки О.
Равенство
-
вектор-радиус точки В,
относительно некоторой неподвижной
точки О.
Равенство
![]() *)
показывает, что траектория точки В
получается из траектории точки
А
путем параллельного перенесения ее на
постоянный по величине и направлению
вектор
.
Следовательно, траектории точек твердого
тела, движущегося поступательно,
представляют тождественные кривые,
получающиеся друг из друга путем
параллельного переноса (АВ||А’В’).
Дифференцируя обе части формулы (*) по
времени и замечая, что производная
постоянного вектора
равна нулю, получим:
*)
показывает, что траектория точки В
получается из траектории точки
А
путем параллельного перенесения ее на
постоянный по величине и направлению
вектор
.
Следовательно, траектории точек твердого
тела, движущегося поступательно,
представляют тождественные кривые,
получающиеся друг из друга путем
параллельного переноса (АВ||А’В’).
Дифференцируя обе части формулы (*) по
времени и замечая, что производная
постоянного вектора
равна нулю, получим:

или,
вспоминая определение вектора скорости:
![]() т. е. скорости
всех точек твердого тела, движущегося
поступательно, в любой момент времени
друг другу равны как по величине, так
и по направлению. Дифференцируя обе
части (2) еще раз по времени, получаем:
т. е. скорости
всех точек твердого тела, движущегося
поступательно, в любой момент времени
друг другу равны как по величине, так
и по направлению. Дифференцируя обе
части (2) еще раз по времени, получаем:
![]() т. е. ускорения
всех точек поступательно движущегося
твердого тела в любой момент времени
одинаковы. Из доказанного следует, что
поступательное движение твердого тела
вполне, определяется движением
какой-нибудь одной из его точек;
следовательно, для изучения поступательного
движения тела достаточно знания
кинематики точки.
т. е. ускорения
всех точек поступательно движущегося
твердого тела в любой момент времени
одинаковы. Из доказанного следует, что
поступательное движение твердого тела
вполне, определяется движением
какой-нибудь одной из его точек;
следовательно, для изучения поступательного
движения тела достаточно знания
кинематики точки.
Глава 5. Вращение твердого тела вокруг неподвижной оси.
§ 1 Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси.
Рассмотрим
движение твердого тела, при котором две
точки его остаются неподвижными; такое
движение представляет вращение тела
вокруг проходящей через неподвижные
точки прямой, называемой осью вращения.
Пусть ось вращения тела совпадает с
осью Oz.
Чтобы определить положение тела,
проведем через ось Oz
две полуплоскости: подвижную Q,
твердо связанную с вращающимся телом,
и неподвижную
Р (рис. 25).
Заданием двугранного угла φ(t)
между этими полуплоскостями положение
твердого тела вполне определяется.
Т раекторией
любой точки М
твердого тела, вращающегося вокруг
неподвижной оси, является окружность
(рис. 25), расположенная в плоскости,
проведенной через М
перпендикулярно к оси вращения; центр
этой окружности находится в пересечении
только что упомянутой плоскости и оси
вращения; радиус окружности равен
расстоянию h
точки М
от оси вращения. Дуга S(t),
отсчитанная от начального положения
Мо
точки до положения ее М
в момент
t,
соответствующая углу поворота
φ, равна
S(t)=hφ(t).
Направляя, как всегда, касательную к
траектории точки, в данном случае
окружности, в сторону возрастания дуги,
определим скорость в проекции ее на
касательную:
раекторией
любой точки М
твердого тела, вращающегося вокруг
неподвижной оси, является окружность
(рис. 25), расположенная в плоскости,
проведенной через М
перпендикулярно к оси вращения; центр
этой окружности находится в пересечении
только что упомянутой плоскости и оси
вращения; радиус окружности равен
расстоянию h
точки М
от оси вращения. Дуга S(t),
отсчитанная от начального положения
Мо
точки до положения ее М
в момент
t,
соответствующая углу поворота
φ, равна
S(t)=hφ(t).
Направляя, как всегда, касательную к
траектории точки, в данном случае
окружности, в сторону возрастания дуги,
определим скорость в проекции ее на
касательную:
 (28)
(28)
величина
h
вынесена за знак производной по времени
как расстояние точки до оси, не
изменяющееся при вращении твердого
тела. Величину ω
назовём угловой скоростью вращения
тела. Скорость любой точки тела,
вращающегося вокруг неподвижной
оси, равна произведению угловой скорости
тела на расстояние точки до оси
вращения. Направление вектора скорости
![]() определится касательной к окружности,
по которой движется точка. Таким образом,
можно установить следующий закон
распределения скоростей в теле,
вращающемся вокруг неподвижной оси: в
данный момент времени скорости различных
точек тела пропорциональны их
расстояниям от оси вращения и направлены
в сторону вращения тела перпендикулярно
к плоскостям, проходящим через ось
вращения и рассматриваемые точки.
определится касательной к окружности,
по которой движется точка. Таким образом,
можно установить следующий закон
распределения скоростей в теле,
вращающемся вокруг неподвижной оси: в
данный момент времени скорости различных
точек тела пропорциональны их
расстояниям от оси вращения и направлены
в сторону вращения тела перпендикулярно
к плоскостям, проходящим через ось
вращения и рассматриваемые точки.
При вычислении линейных скоростей точек вращающегося тела по формуле (28) необходимо помнить, что угловая скорость должна быть выражена в рад/сек, (1/сек). Перейдем к рассмотрению ускорений точек тела, вращающегося вокруг неподвижной оси. Воспользуемся для этого формулами проекций ускорения на касательную и главную нормаль к траектории - и данном случае окружности радиуса h:
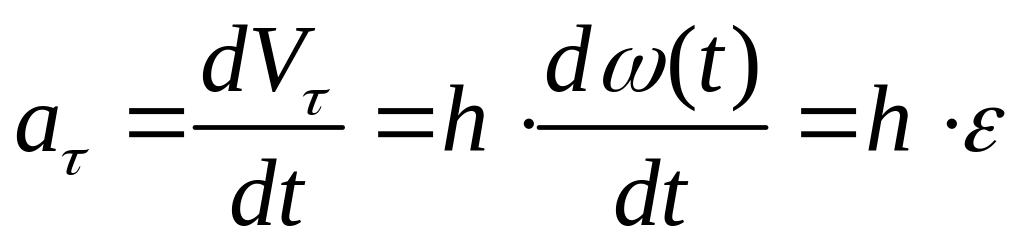 ,
, (2.9)
(2.9)
з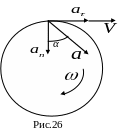 десь
обозначено
десь
обозначено
 ,
где через ε
обозначено угловое ускорение. Касательную
и нормальную составляющие ускорения
принято называть соответственно
вращательной и осестремительной
составляющими ускорения, или кратко
вращательным и осестремительным
ускорениями.
,
где через ε
обозначено угловое ускорение. Касательную
и нормальную составляющие ускорения
принято называть соответственно
вращательной и осестремительной
составляющими ускорения, или кратко
вращательным и осестремительным
ускорениями.
Осестремительная проекция ускорения, как видно из последней формулы, всегда положительна, т.е. осестремительное ускорение всегда направлено по радиусу окружности от точки к оси вращения. Что же касается вращательной составляющей, то она направлена по касательной в сторону положительного отсчета углов (и дуг), если ε > 0, и в противоположную сторону при ε < 0. На рис. 26 показано взаимное расположение вращательного и центростремительного ускорений и скорости при одном и том же направлении вращения тела. Полное ускорение точки вращающегося тела
![]() ,
,
угол
α,
образованный вектором ускорения
![]() (рис. 26) с направлением нормали к
траектории:
(рис. 26) с направлением нормали к
траектории:
 .
.
Таким образом, приходим к следующему закону распределения ускорений в твердом теле, вращающемся вокруг неподвижной оси: в данный момент времени ускорения точек тела пропорциональны расстояниям точек от оси вращения и наклонены под одинаковыми углами к радиусам вращения.
Рассмотрим пример. Сравним скорости и ускорения на ободе маховика паровой машины, имеющего диаметр D=l,5м и вращающегося с угловой скоростью N =240 об/мин, и турбинного диска, имеющего диаметр 10 см и совершающего 18 000 об/мин.
В
первом случае
![]() ,
h=D/2=0.75
м
и,
следовательно, V=0,75•8π=18,85м/сек
,
h=D/2=0.75
м
и,
следовательно, V=0,75•8π=18,85м/сек
![]() .
Окружная скорость и центростремительное
ускорение точки обода турбинного
диска будут:
.
Окружная скорость и центростремительное
ускорение точки обода турбинного
диска будут:
 ,
,
![]()
Ускорение
частицы на ободе диска в 126000 раз
превосходит ускорение силы тяжести
g=9,81
![]() .
.
