
- •Глава 4.
- •Глава 6.
- •Глава 9.
- •Глава 10.
- •Глава 11.
- •Глава 12.
- •Глава 13.
- •Глава 14.
- •Глава 15.
- •Глава 16
- •Глава 18
- •Глава 1.
- •§ 1. Аксиомы и принципы статики твёрдого тела.
- •§ 2. Момент силы относительно произвольного центра, оси.
- •§ 3. Пара сил и её свойства.
- •§ 4.Главный вектор и главный момент системы сил. Правило Пуансо.
- •§ 5. Приведение системы сил к простейшему виду.
- •§ 6. Уравнения равновесия тела.
- •Глава 2. Центр параллельных сил и центр тяжести.
- •§ 1. Центр параллельных сил.
- •§ 2. Центр тяжести, методы определения координат центра тяжести.
- •Глава 3. Равновесие при наличии сил трения.
- •§ 1. Трение скольжения Угол трения, конус трения.
- •§ 2. Задача об опрокидывании тела. Трение качения.
- •Кинематика
- •Глава 4. Кинематика точки.
- •§ 1. Способы задания движения точки. Уравнения движения точки; траектория.
- •§ 2. Натуральный триэдр траектории.
- •§ 3. Скорость точки.
- •§ 4. Ускорение точки.
- •§ 5. Поступательное движение твердого тела.
- •Глава 5. Вращение твердого тела вокруг неподвижной оси.
- •§ 1 Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси.
- •§ 2. Векторные формулы скорости и ускорения точек тела, вращающегося вокруг неподвижной оси.
- •Глава 6. Кинематика плоского движения твердого тела
- •§ 1. Уравнения плоского движения.
- •§ 2. Скорости точек плоской фигуры.
- •§ 3. Мгновенный центр скоростей плоской фигуры.
- •§ 4. Ускорения точек плоской фигуры.
- •Глава 4. Вращение тела вокруг неподвижной точки. Общий случай движения тела.
- •§ 1. Определение положения твердого тела, имеющего неподвижную точку.
- •§ 2 Углы Эйлера, матрицы поворота.
- •§ 3. Угловая скорость и угловое ускорение твердого тела, имеющего неподвижную точку.
- •§ 4. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижного центра.
- •Глава 6.
- •§ 5. Определение положения твердого тела в пространстве.
- •§ 6. Скорости и ускорения в общем случае движения твердого тела.
- •Глава 8. .Кинематика относительного движения точки и тела.
- •§ 1. Абсолютное, относительное и переносное движения.
- •§ 2. Теорема о сложении скоростей в относительном движении.
- •§ 3. Сложение ускорений, теорема Кориолиса.
- •§ 4. Сложение вращений твёрдого тела.
- •§ 5. Общий случай движения тела (для скоростей).
- •Динамика точки и твёрдого тела
- •Глава 9. Динамика точки.
- •§ 1. Основные положения и аксиомы динамики
- •§ 2. Дифференциальные уравнения движения материальной точки.
- •§ 3. Динамики относительного движения точки.
- •Глава 10. Количество движения системы.
- •§ 1. Уравнения динамики системы материальных точек и твёрдого тела.
- •§ 2. Теорема об изменении количества движения системы материальных точек.
- •§ 3. Теорема о движении центра масс.
- •Глава 11. Кинетический момент системы и твёрдого тела.
- •§ 1. Теорема об изменении главного момента количества движения системы материальных точек.
- •§ 3. Кинетический момент тела, вращающегося относительно неподвижной точки.
- •§ 3. Момент инерции относительно произвольной оси. Тензор инерции.
- •§ 4. Главные оси инерции и главные моменты инерции.
- •§ 5. Вычисление моментов инерции.
- •§ 6. Преобразование моментов инерции.
- •§ 7. Кинетический момент твердого тела.
- •Глава 12. Дифференциальные уравнения движения твердого тела.
- •§ 1. Дифференциальные уравнения вращения твердого тела.
- •§ 2. Общий случай движения твердого тела.
- •§ 3. Динамика плоско-параллельного движения тела.
- •§ 4. Реакция оси вращающегося тела.
- •§ 5. Задача о физическом маятнике.
- •Глава 13. Кинетическая энергия системы и твёрдого тела.
- •§ 1. Кинетическая энергия системы материальных точек.
- •§ 2. Кинетическая энергия твердого тела.
- •§ 3. Работа силы. Мощность.
- •§ 4. Примеры вычисления потенциальной энергии и работы
- •§ 5. Теорема об изменении кинетической энергии.
- •§ 6. Закон сохранения механической энергии.
- •Динамика несвободной системы. __________________________________________________________Глава 14. Возможные перемещения.
- •§1. Связи, классификация связей, число степеней свободы.
- •§2. Возможные перемещения.
- •§ 3. Принцип освобождаемости. Идеальные связи.
- •§ 4. Статический принцип возможных перемещений.
- •§ 5. Динамический принцип возможных перемещений. Общее уравнение динамики.
- •Глава 15. Уравнение Лагранжа второго рода и его приложения.
- •§ 1. Вывод уравнения Лагранжа второго рода.
- •§ 2. Диссипативная функция.
- •§ 8. Представление кинетической энергии как функции обобщённых скоростей.
- •§ 9. Интеграл энергии.
- •Малые колебания системы с одной степенью свободы.
- •Глава 16 Свободные колебания системы с одной степенью свободы.
- •§ 1. Устойчивость равновесия голономной системы в консервативном силовом поле.
- •§ 2. Малые свободные колебания системы с одной степенью свободы.
- •§ 3. Свободные колебания системы с учётом линейно-вязкого сопротивления.
- •Глава 17.
- •§ 1. Вынужденные колебания без сопротивления. Биения, резонанс.
- •§ 2. Вынужденные колебания системы с учётом линейно-вязкого трения.
- •§ 3. Динамические характеристики вынужденных колебаний.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Глава 18 Уравнения статики деформируемого твёрдого тела.
- •§ 1. Дифференциальные уравнения равновесия нерастяжимой нити.
- •§ 2. Статика деформируемых прямых стержней.
- •Глава 19. Элементарная теория удара
- •§ 1. Теорема импульсов и её приложения в теории удара.
- •§ 2. Задача Герца о прямом и центральном ударе двух тел.
- •§ 3. Теоремы об изменении количества движения и кинетического момента при ударе.
- •§ 4. Удар, действующий на тело, вращающегося вокруг неподвижной оси.
- •§ 5. Условия отсутствия ударных реакций. Центр удара.
- •1.Статика.
- •2. Кинематика.
- •3. Динамика точки и твердого тела:
- •4. Динамика несвободной системы.
- •5. Колебания системы около положения устойчивого равновесия.
- •Дополнительные вопросы, включаемые по согласованию с выпускающими кафедрами: Динамические характеристики вынужденных колебаний. Нелинейные колебания точки. Метод Ван дер Поля.
- •3. Теорема о движении центра масс.
- •6. Теорема об изменении кинетической энергии.
§ 2. Натуральный триэдр траектории.
П режде
всего несколько разовьем ранее сказанное
о вектор-функции и ее производной. Пусть
режде
всего несколько разовьем ранее сказанное
о вектор-функции и ее производной. Пусть
![]() -
непрерывная вектор-функция скалярного
аргумента
u, геометрически
изображаемая своим годографом, т. е.
траекторией конца N
векторов
при непрерывно изменяющихся значениях
аргумента u,
и начало этих векторов откладывается
от некоторого полюса О
(Рис 19).
Производная от вектор – функции
-
непрерывная вектор-функция скалярного
аргумента
u, геометрически
изображаемая своим годографом, т. е.
траекторией конца N
векторов
при непрерывно изменяющихся значениях
аргумента u,
и начало этих векторов откладывается
от некоторого полюса О
(Рис 19).
Производная от вектор – функции
![]() по
скалярному аргументу u,
определяется как предел
по
скалярному аргументу u,
определяется как предел
 (2.1)
(2.1)
и представляет вектор, имеющий направление
касательной к годографу, проведенной
в сторону, соответствующую возрастанию
аргумента u.
Вектор
характеризует быстроту изменения по
величине и направлению вектора
с изменением аргумента u.
представляет вектор, имеющий направление
касательной к годографу, проведенной
в сторону, соответствующую возрастанию
аргумента u.
Вектор
характеризует быстроту изменения по
величине и направлению вектора
с изменением аргумента u.
Величину
или модуль производной будем обозначать
через
![]() .
Модуль производной вектора не равен
значению производной его модуля.
.
Модуль производной вектора не равен
значению производной его модуля.
![]() (2.2)
(2.2)
При дифференцировании векторов сохраняются те же правила, что и при дифференцировании функций:
производная геометрической суммы (разности) вектор–функции равна геометрической сумме (разности) производных. Точно так же сохраняется и правило дифференцирования произведения скалярной функции X (u) на вектор :
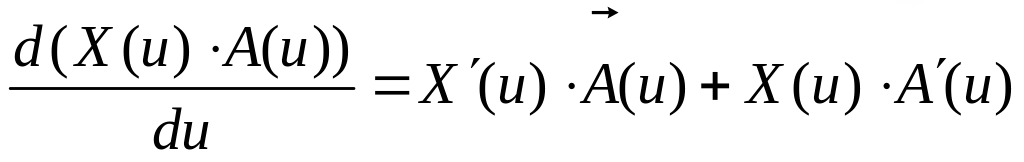
Понятие
вектор – функции и её производной
облегчают рассмотрение основных
геометрических свойств траектории,
необходимых для развития представления
о скорости и ускорения точки. Рассмотрим
некоторую кривую, лежащую (вообще говоря)
не в одной плоскости. Возьмём на этой
кривой три точки М1,
М2 и
М. Проведём
через эти три точки плоскость
(предполагается, что три точки не лежат
на одной прямой). Устремим точки
М1 и М2
к точке М.
Проведённая плоскость при этом будет
каким – то образом поворачиваться и
займёт предельное положения, когда все
три точки сольются. Это предельное
положение назовём соприкасающейся
плоскостью (СП), в которой проведём
касательную к кривой в точке М.
Орт касательной в точке М
обозначим
![]() .
Проведем в точке М
плоскость перпендикулярную к орту
,
эту плоскость назовём нормальной
плоскостью (НП) кривой. Любая прямая,
проведенная в этой плоскости через
точку М,
будет перпендикулярна к
,
т. е. будет нормалью кривой; линия
пересечения нормальной и соприкасающейся
плоскостей определяет главную нормаль
кривой. Иными словами, главной нормалью
называется нормаль, лежащая в
соприкасающейся плоскости. Нормаль,
перпендикулярная к главной нормали,
называется бинормалью кривой. Если, в
частности, кривая — плоская, то
соприкасающейся плоскостью будет
плоскость, в которой расположена кривая,
а главной нормалью — нормаль кривой,
лежащая в этой плоскости.
.
Проведем в точке М
плоскость перпендикулярную к орту
,
эту плоскость назовём нормальной
плоскостью (НП) кривой. Любая прямая,
проведенная в этой плоскости через
точку М,
будет перпендикулярна к
,
т. е. будет нормалью кривой; линия
пересечения нормальной и соприкасающейся
плоскостей определяет главную нормаль
кривой. Иными словами, главной нормалью
называется нормаль, лежащая в
соприкасающейся плоскости. Нормаль,
перпендикулярная к главной нормали,
называется бинормалью кривой. Если, в
частности, кривая — плоская, то
соприкасающейся плоскостью будет
плоскость, в которой расположена кривая,
а главной нормалью — нормаль кривой,
лежащая в этой плоскости.
Совокупность трех взаимно перпендикулярных осей: 1) касательной, направленной в сторону возрастания дуги, 2) главной нормали, направленной в сторону вогнутости кривой, и 3) бинормали, перпендикулярной к касательной и главной нормали образует так называемый натуральней триэдр кривой.
Единичные
векторы этих осей обозначим соответственно
через
![]() .
Найдем выражения этих трех единичных
векторов натурального триэдра через
вектор-радиус точки на кривой, заданный
как вектор-функция дуги:
.
Найдем выражения этих трех единичных
векторов натурального триэдра через
вектор-радиус точки на кривой, заданный
как вектор-функция дуги:
![]() .
Найдем прежде всего
.
По определению векторной производной
вектор
.
Найдем прежде всего
.
По определению векторной производной
вектор
![]() направлен
по касательной к годографу вектора
направлен
по касательной к годографу вектора
![]() в сторону возрастания дуги S.
С другой стороны, численная величина
производной равна
в сторону возрастания дуги S.
С другой стороны, численная величина
производной равна
 .
Таким образом, векторная производная
представляет искомый единичный вектор
касательной
.
Таким образом, векторная производная
представляет искомый единичный вектор
касательной
![]() (2.3)
(2.3)
Д ля
определения единичного вектора главной
нормали
ля
определения единичного вектора главной
нормали
![]() обратимся к рис. 20 и рис. 21. Р
обратимся к рис. 20 и рис. 21. Р![]() ,
с тем меньшей ошибкой, чем меньше ΔS,
можно считать перпендикулярным к
и, следовательно, параллельным вектору
нормали
,
с тем меньшей ошибкой, чем меньше ΔS,
можно считать перпендикулярным к
и, следовательно, параллельным вектору
нормали
![]() ,
лежащему с
в
одной и той же плоскости. По абсолютной
величине
(как основание равнобедренного
треугольника с малым углом α
при вершине и боковыми сторонами,
равными единице) будет равен
,
лежащему с
в
одной и той же плоскости. По абсолютной
величине
(как основание равнобедренного
треугольника с малым углом α
при вершине и боковыми сторонами,
равными единице) будет равен
 Отсюда
найдем (с точностью до малых высших
порядков):
Отсюда
найдем (с точностью до малых высших
порядков):
![]() или
или
 .
Будем
приближать ΔS
к нулю, тогда точка M1
будет стремиться к М,
единичный вектор нормали
— к искомому единичному вектору
,
и мы будем иметь:
.
Будем
приближать ΔS
к нулю, тогда точка M1
будет стремиться к М,
единичный вектор нормали
— к искомому единичному вектору
,
и мы будем иметь:
 .
Второй множитель определяет кривизну
кривой в данной точке, величина обратная
кривизне – ρ
называется радиусом кривизны
.
Второй множитель определяет кривизну
кривой в данной точке, величина обратная
кривизне – ρ
называется радиусом кривизны

Таким
образом, имеем следующее выражение орта
главной нормали
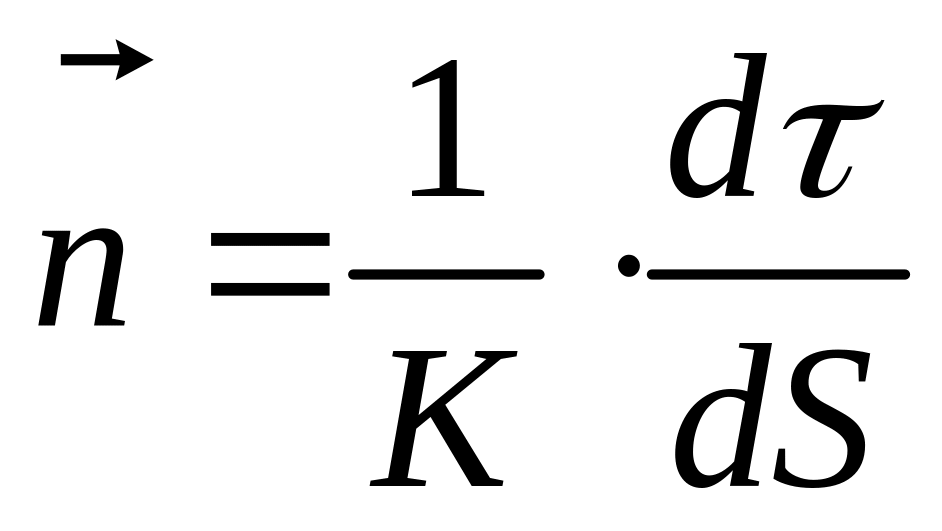 .
Или в более
привычной записи
.
Или в более
привычной записи
 (2.4)
(2.4)
