4.2. Правила дифференцирования. Производные основных элементарных функций. Производная обратной функции.

На основании определения производной и теорем о вычислении пределов (раздел 2.3), можно установить следующие правила дифференцирования.

Пусть и дифференцируемы в точке . Тогда в той же точке дифференцируемы их сумма, произведение, а если , то и частное , причем

1). , ;

2). , ; (4.9)

3). , , .

4). Производная сложной функции. Пусть функция дифференцируема в точке , а дифференцируема в точке , тогда сложная функция дифференцируема в точке , причём

или (4.10)

Основываясь на определении производной, правилах вычисления пределов, а также правилах (4.9) и (4.10), можно найти производные основных элементарных функций:

1. , ;

2. , , ;

3. , ;

4. , ;

5. , ;

, ; (4.11)

6. , , ;

, ;

7. , ;

8. , .

Из правила 2 и соотношения 1 формул (4.11) следует

5) , ,

а из правила 1 и предыдущего правила следует

6) , ;

Пример 4.4. Найти производные функций:

(а) , .

(б) ,

(в) , ;

(г) . Эта функция сложная: , .

Поскольку , , то согласно (4.10), получим:

(д) . Перепишем функцию в форме

, откуда

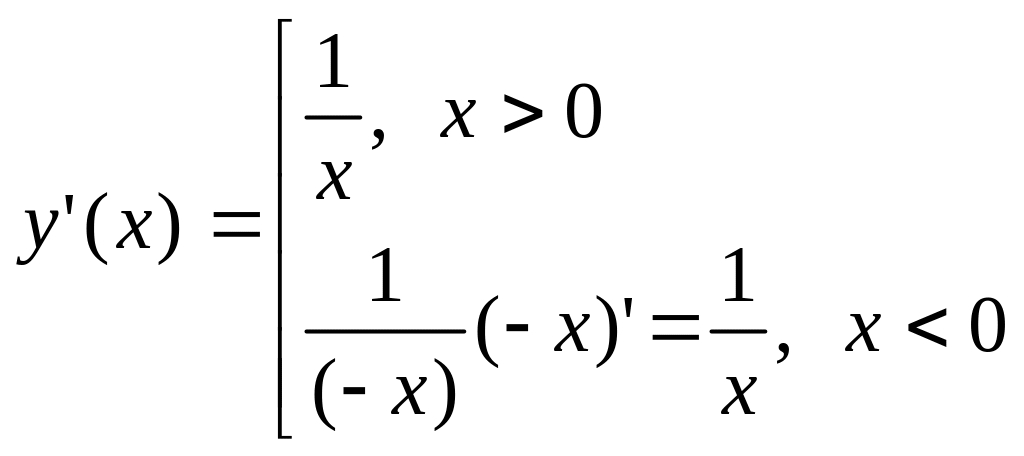
т.е. для всех , отличных от нуля.

Производная обратной функции. Пусть для функции существует обратная , причём существует и отлична от нуля. Тогда в точке существует производная обратной функции , причём

или (4.12)

Пример 4.5. Найдём производную функции , которая является обратной для функции при , причём в интервале . Согласно (4.12), , а так как при , , то .

Проводя аналогичные выкладки, таблицу производных можно дополнить:

9. , ;

10. , ; (4.13)

11. , ;

12. , .

4.3. Производная функции, заданной параметрически. Производная неявной функции. Производные высших порядков.

Определение. Говорят, что функция задана параметрически, если она определяется двумя функциями аргумента , называемого параметром:

(4.14)

и при этом для функции существует обратная . Параметр существует на некотором множестве (например, на отрезке ).

Заметим, что если обратить первое соотношение (4.14) и подставить этот результат во втором соотношение, получится равенство, определяющие сложную функцию в форме

(4.15)

Если и дифференцируемы в некоторой области изменения , причём , то производная находится по формуле:

. (4.16)

Как видим, для того, чтобы найти , вовсе незачем обращать функцию и строить соотношение (4.15).

Пример 4.6. , (  некоторые числа).

Согласно (4.16)

.

Определение. Пусть переменные и связаны уравнением

. (4.17)

Если каждому значению переменной , изменяющейся на множестве (например, интервале или отрезке) соответствует одно и только одно значение , удовлетворяющее вместе с уравнению (4.17), то говорят, что это уравнение определяет неявную функцию .

Заметим, что одно уравнение (4.17) может определять не одну, а несколько неявных функций. Заметим также, что далеко не всегда уравнение (4.17) можно разрешить относительно .

Пример 4.7.

Для того, чтобы найти производную неявной функции, совсем не обязательно разрешать уравнение (4.17) относительно . Для этого достаточно воспользоваться следующей методикой:

1) Вычислить производную по левой части (4.17) как производную сложной функции ;

2) Приравнять эту производную нулю: ;

3) Разрешить получившееся уравнение относительно , при этом будет зависеть как от , так и от .

Пример 4.8. , где  некоторое число;

, откуда

Определение. Производная от производной функции называется второй производной (или производной второго порядка) этой функции. Её обозначение: или .

Пример 4.9. , , .

Аналогично определяются производные третьего порядка, четвёртого и т.д.