
- •Содержание
- •Глава 1 понятие функции
- •1.1. Понятие функции, способы её задания. Последовательность
- •Различают три основных способа задания функции.
- •1 .2. Основные элементарные функции
- •Глава 2 предел функции
- •2.1. Предел функции, односторонний предел. Предел последовательности.
- •2.2. Понятия бесконечно малой и бесконечно большой функций. Ограниченная функция.
- •Свойство бесконечно малых и бесконечно больших функций.
- •2.3. Основные теоремы о пределах. Первый и второй замечательные пределы. Сравнение бесконечно малых.
- •Сравнение бесконечно малых.
- •Глава 3 непрерывность функции
- •3.1. Непрерывность функции в точке. Разрывная функция. Классификация точек разрыва.
- •3.2. Теоремы о непрерывных функциях
- •3.3. Свойства функций, непрерывных на отрезке.
- •Глава 4 производная
- •4 .1. Понятие производной, её физический и геометрический смысл. Дифференциал функции.
- •4.2. Правила дифференцирования. Производные основных элементарных функций. Производная обратной функции.
- •4.3. Производная функции, заданной параметрически. Производная неявной функции. Производные высших порядков.
- •4.4. Теоремы о дифференцируемых функциях. Правило Лопиталя.
- •Глава 5 исследование поведения функций.
- •5.1. Возрастание и убывание функций.
- •5.2. Экстремумы функций. Наибольшее и наименьшее значения функции на отрезке.
- •5.3. Выпуклость графика функции. Точки перегиба.
- •5.4. Асимптоты графика функции. Общее исследование функций и построение графиков.
- •Глава 6 рекомендуемые задачи
- •6.1. Построение графиков функций без применения методов дифференциального исчисления
- •6.2. Задачи на вычисление предела последовательности
- •6.3. Задачи на вычисление предела функции
- •6.4. Исследование функции на непрерывность
- •6.5. Найти производные функций
- •6.6. Задачи на вычисление пределов функций с использованием правила Лопиталя
- •6.7. Исследование поведения функций с помощью производных
- •Глава 7 варианты расчетно-графических работ
- •7.1. Построить графики функций без применения методов дифференциального исчисления
- •7.2. Вычислить предел последовательности
- •7.3. Вычислить предел функции
- •7.4. Исследовать функцию на непрерывность
- •7.5. Найти производные функций
- •7.6. Вычислить предел функции с использованием правила Лопиталя
- •7.7. Исследовать поведение функции с помощью методов дифференциального исчисления
- •Литература
- •Для заметок
7.4. Исследовать функцию на непрерывность
Найти точки разрыва (если они есть), указать их тип и построить эскиз графика функции в окрестности каждой из этих точек.
Вариант 1
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
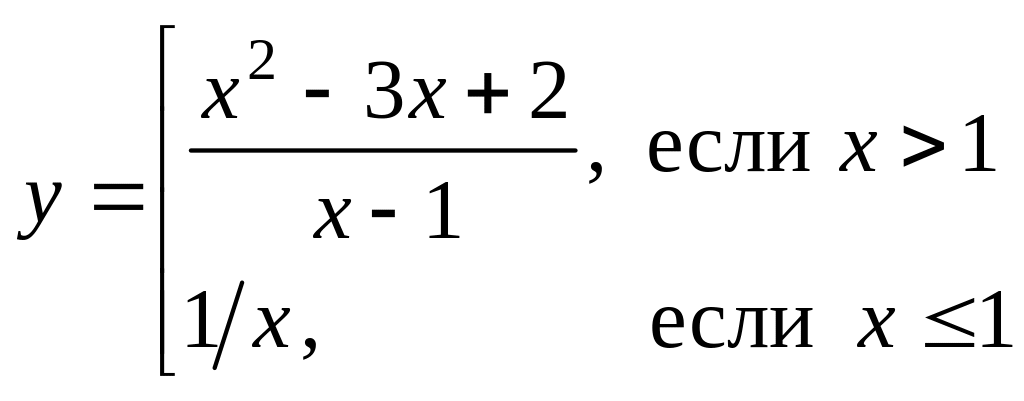
Вариант 2
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
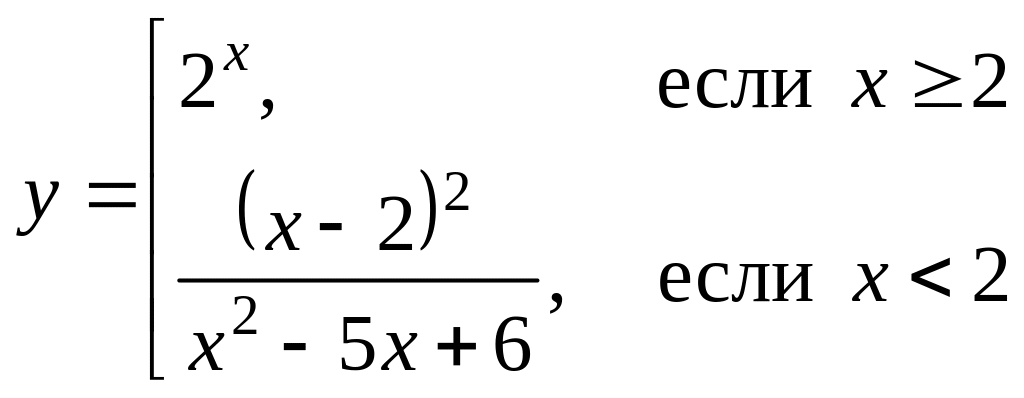
Вариант 3
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
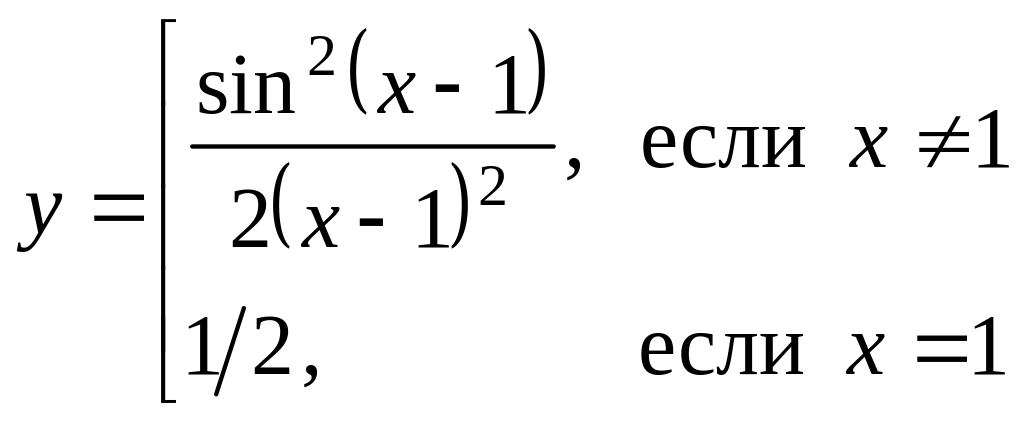
Вариант 4
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
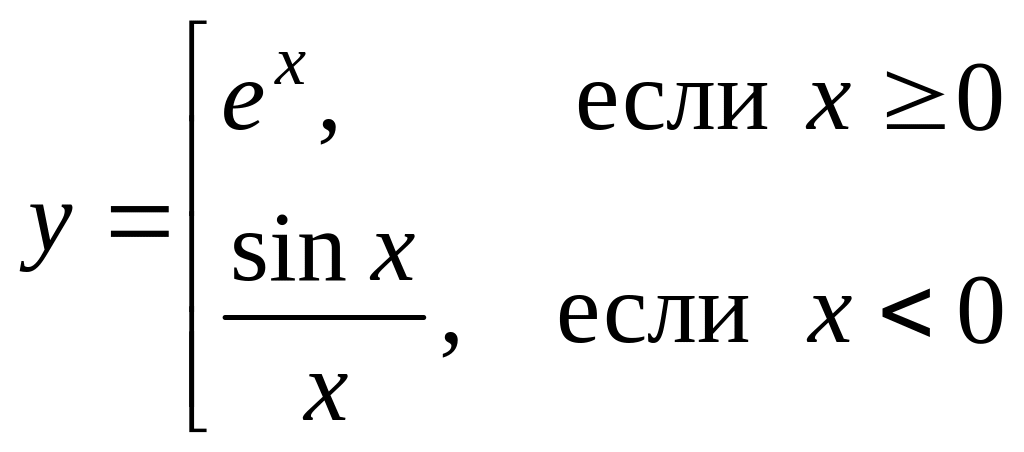
Вариант 5
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 6
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
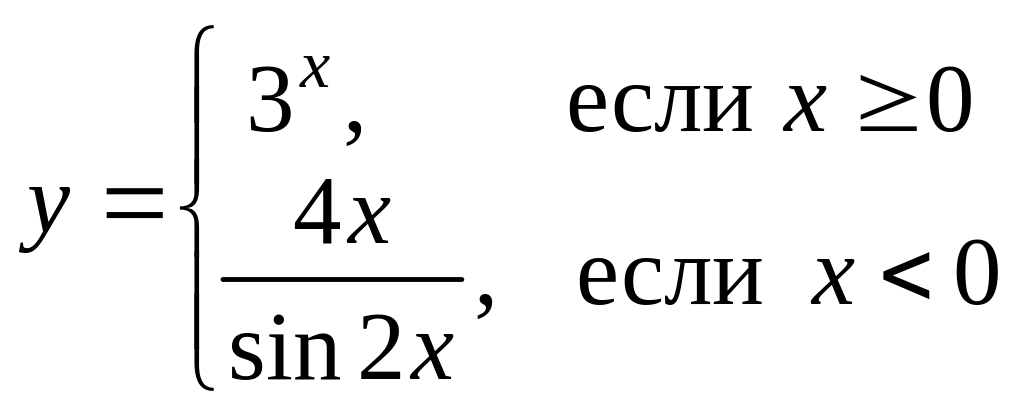
Вариант 7
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
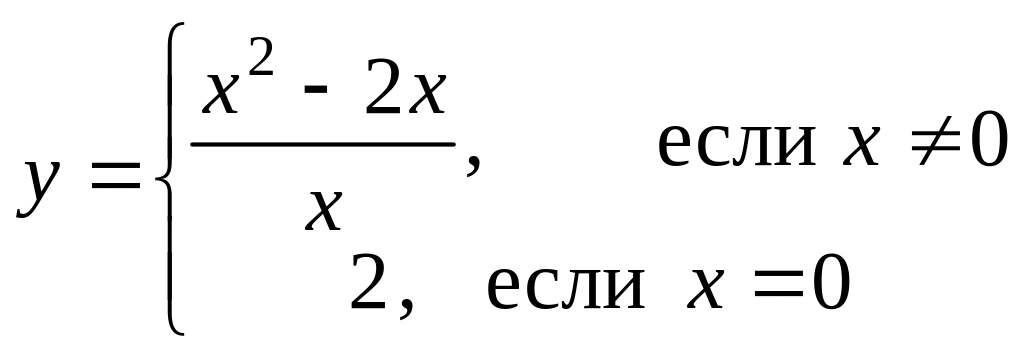
Вариант 8
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
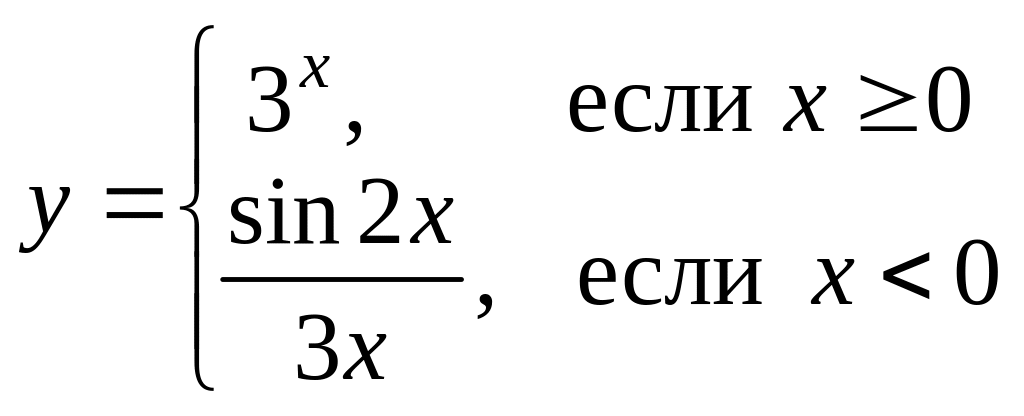
Вариант 9
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
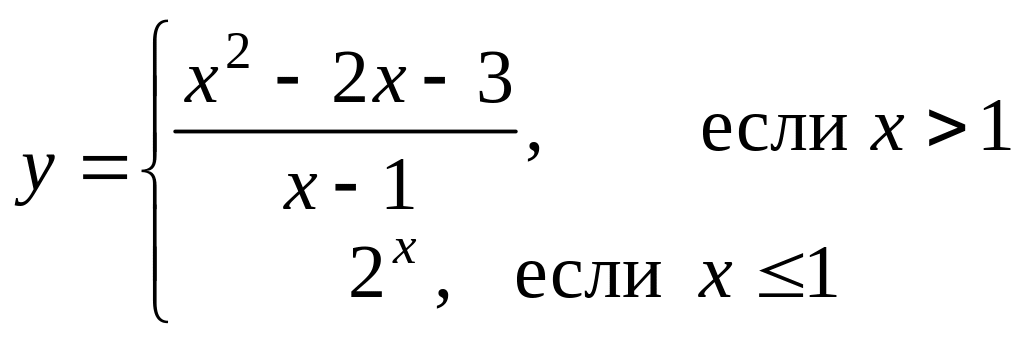
Вариант 10
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
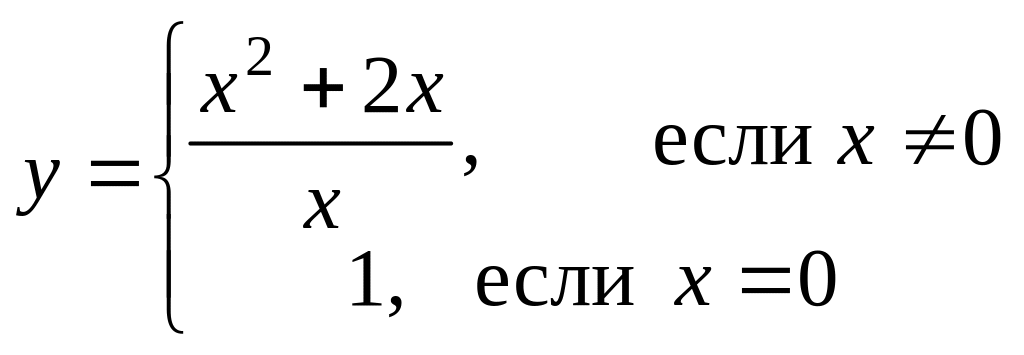
Вариант 11
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
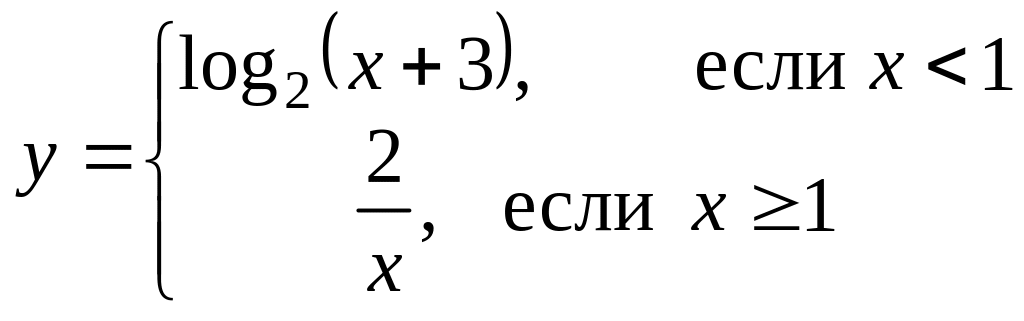
Вариант 12
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)

Вариант 13
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 14
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 15
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
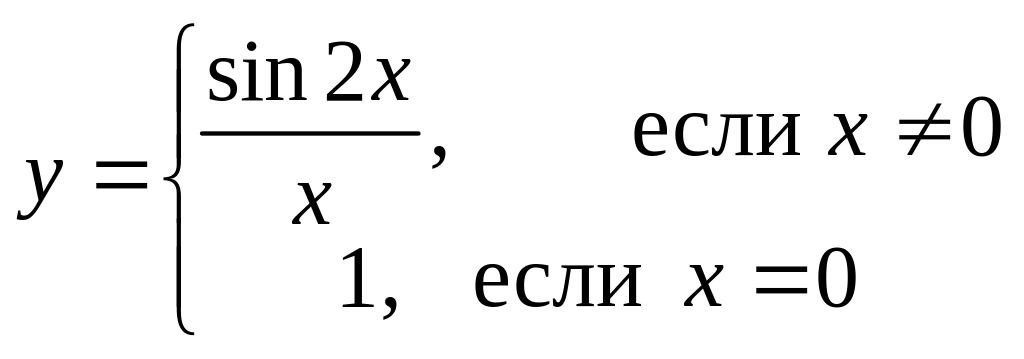
Вариант 16
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
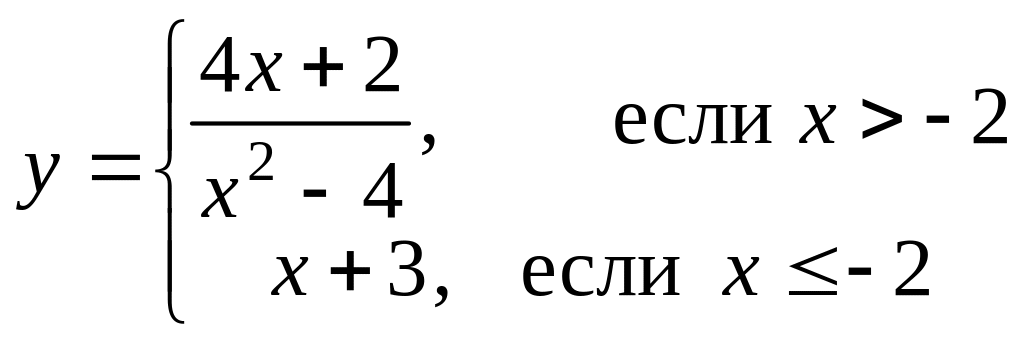
7.5. Найти производные функций
Для функции
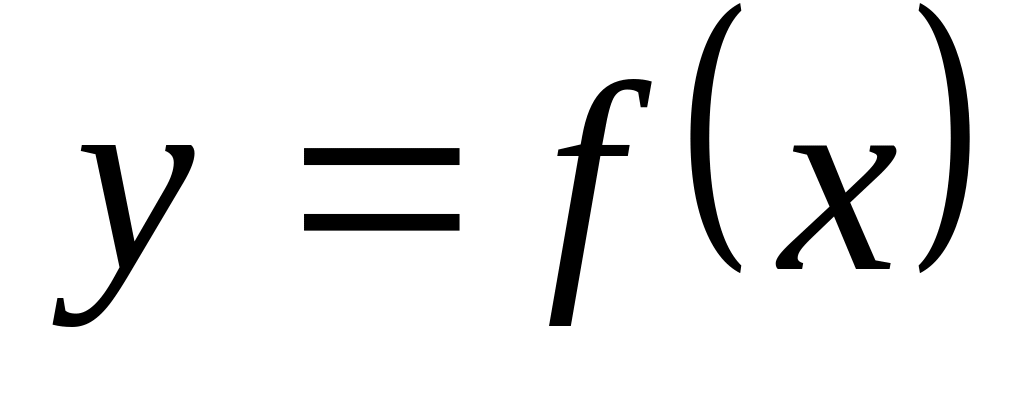 найти первую и вторую производные.
найти первую и вторую производные.Найти производную
 функции, заданной параметрически.
функции, заданной параметрически.Найти производную функции, заданной неявно.
Написать уравнения касательной и нормали к графику функции
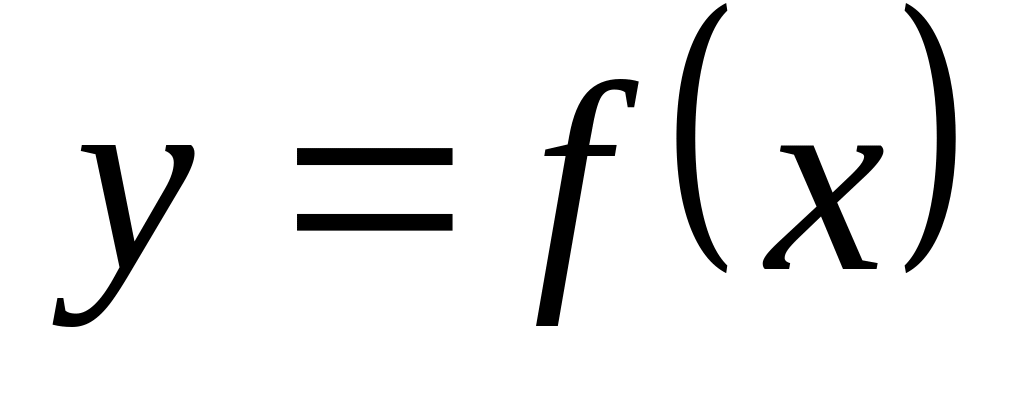 в точке
в точке
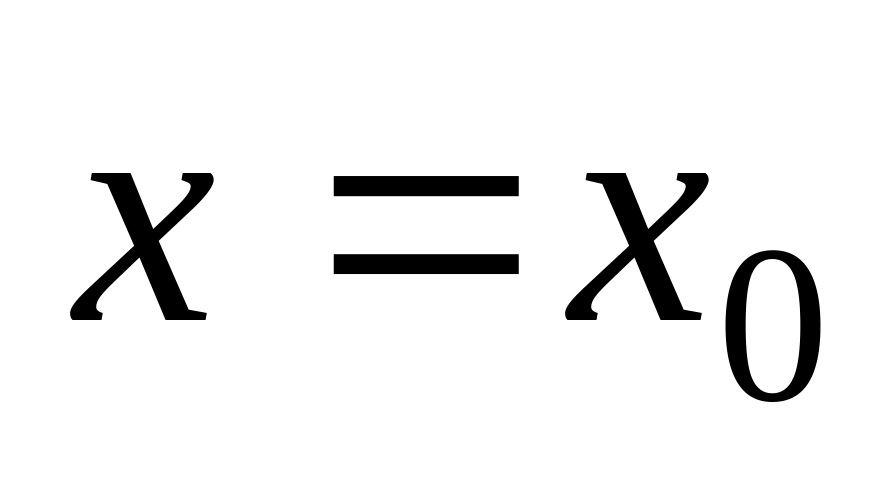 .
.Вычислить приближенно с помощью дифференциала функции.
Вариант 1
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)![]()
Вариант 2
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 3
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 4
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 5
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 6
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 7
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 8
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 9
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 10
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 11
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 12
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 13
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 14
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 15
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 16
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
7.6. Вычислить предел функции с использованием правила Лопиталя
Вариант 1
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 2
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 3
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 4
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 5
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 6
1)
![]() 2)
2)
![]() 3)
3)
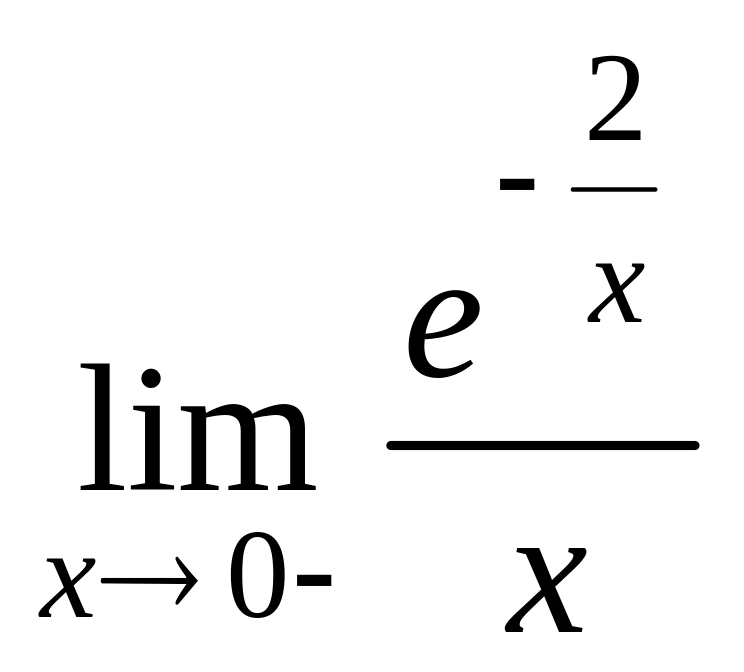
4)
![]() 5)
5)
![]()
Вариант 7
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 8
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 9
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 10
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 11
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант12
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 13
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 14
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 15
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 16
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
7.7. Исследовать поведение функции с помощью методов дифференциального исчисления
Найти области убывания и возрастания функции, а также исследовать её на экстремумы.
Найти наибольшее и наименьшее значения функции на заданном отрезке.
Найти интервалы выпуклости и точки перегиба графика функции (если они есть).
Найти асимптоты графика функции.
5), 6) Провести полное исследование функции и построить ее график.
Вариант 1
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 2
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 3
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 4
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 5
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 6
1)![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 7
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 8
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 9
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 10
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 11
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 12
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 13
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 14
1)![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 15
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Вариант 16
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
