
- •Содержание
- •Глава 1 понятие функции
- •1.1. Понятие функции, способы её задания. Последовательность
- •Различают три основных способа задания функции.
- •1 .2. Основные элементарные функции
- •Глава 2 предел функции
- •2.1. Предел функции, односторонний предел. Предел последовательности.
- •2.2. Понятия бесконечно малой и бесконечно большой функций. Ограниченная функция.
- •Свойство бесконечно малых и бесконечно больших функций.
- •2.3. Основные теоремы о пределах. Первый и второй замечательные пределы. Сравнение бесконечно малых.
- •Сравнение бесконечно малых.
- •Глава 3 непрерывность функции
- •3.1. Непрерывность функции в точке. Разрывная функция. Классификация точек разрыва.
- •3.2. Теоремы о непрерывных функциях
- •3.3. Свойства функций, непрерывных на отрезке.
- •Глава 4 производная
- •4 .1. Понятие производной, её физический и геометрический смысл. Дифференциал функции.
- •4.2. Правила дифференцирования. Производные основных элементарных функций. Производная обратной функции.
- •4.3. Производная функции, заданной параметрически. Производная неявной функции. Производные высших порядков.
- •4.4. Теоремы о дифференцируемых функциях. Правило Лопиталя.
- •Глава 5 исследование поведения функций.
- •5.1. Возрастание и убывание функций.
- •5.2. Экстремумы функций. Наибольшее и наименьшее значения функции на отрезке.
- •5.3. Выпуклость графика функции. Точки перегиба.
- •5.4. Асимптоты графика функции. Общее исследование функций и построение графиков.
- •Глава 6 рекомендуемые задачи
- •6.1. Построение графиков функций без применения методов дифференциального исчисления
- •6.2. Задачи на вычисление предела последовательности
- •6.3. Задачи на вычисление предела функции
- •6.4. Исследование функции на непрерывность
- •6.5. Найти производные функций
- •6.6. Задачи на вычисление пределов функций с использованием правила Лопиталя
- •6.7. Исследование поведения функций с помощью производных
- •Глава 7 варианты расчетно-графических работ
- •7.1. Построить графики функций без применения методов дифференциального исчисления
- •7.2. Вычислить предел последовательности
- •7.3. Вычислить предел функции
- •7.4. Исследовать функцию на непрерывность
- •7.5. Найти производные функций
- •7.6. Вычислить предел функции с использованием правила Лопиталя
- •7.7. Исследовать поведение функции с помощью методов дифференциального исчисления
- •Литература
- •Для заметок
6.6. Задачи на вычисление пределов функций с использованием правила Лопиталя
Кроме примеров данного раздела см. также примеры 4.9 – 4.13.
Пример 6.35.
![]() (неопределенность вида
(неопределенность вида
![]() ).
).
Решение.
![]() .
.
Пример 6.36.
![]() (неопределенность вида
(неопределенность вида
![]() ).
).
Решение.
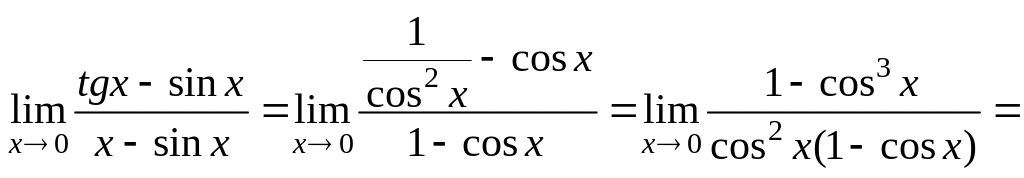
![]()
Пример 6.37.
![]() (неопределенность вида
(неопределенность вида
![]() ).
).
Решение.
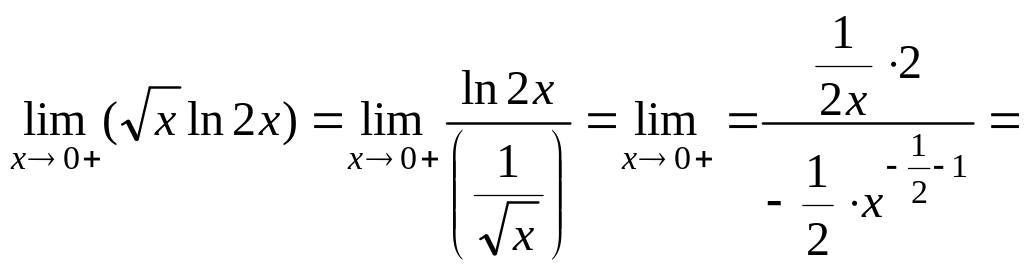
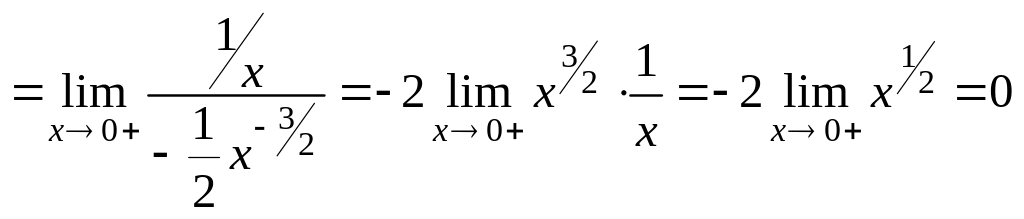 .
.
Пример 6.38.
![]() (неопределенность вида
(неопределенность вида
![]() ).
).
Решение.
Поскольку
![]() ,
то
,
то
![]() .
.
Последнее равенство справедливо в силу непрерывности экспоненциальной функции.
Рассмотрим:
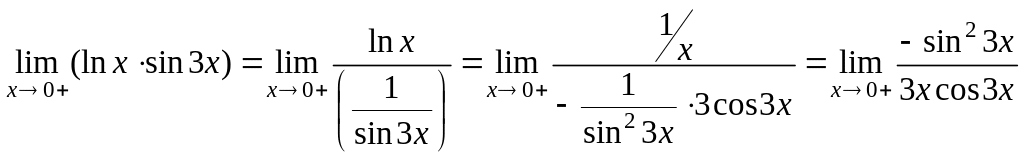
Поскольку при
![]()
![]() ,
то
,
то
![]() ,
в результате чего искомый предел равен
,
в результате чего искомый предел равен
![]() .
.
Пример 6.39.
![]() (неопределенность вида
(неопределенность вида
![]() ).,
).,
Решение.
Так как
![]() ,
то
,
то
![]() .
.
Согласно правилу Лопиталя
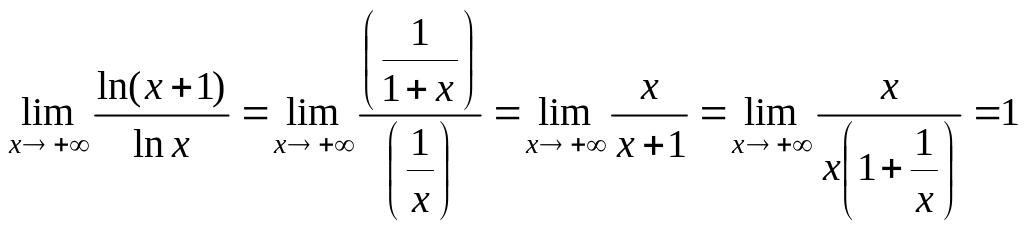 ,
,
поэтому искомый предел равен
![]() .
.
6.7. Исследование поведения функций с помощью производных
Кроме примеров данного раздела см. также примеры 5.1 – 5.12.
Пример 6.40.
Найти области убывания и возрастания
функции
![]() ,
а также исследовать ее на экстремум.
,
а также исследовать ее на экстремум.
Решение. Данная функция определена (и является непрерывной) на всей числовой оси, за исключением точки , в которой она имеет разрыв 2-го рода. Найдем производную
![]() .
.
К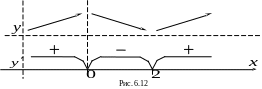 ритической
точкой, в которой
ритической
точкой, в которой
![]() ,
является
,
является
![]() .
Для исследования знаков
применим метод интервалов. На рис. 6.12
указан знак производной
на каждом из интервалов ее знакопостоянства.
Там же указан характер монотонности
заданной функции
,
соответствующий знаку
.
.
Для исследования знаков
применим метод интервалов. На рис. 6.12
указан знак производной
на каждом из интервалов ее знакопостоянства.
Там же указан характер монотонности
заданной функции
,
соответствующий знаку
.
Таким образом,
при
![]() монотонно возрастает; при
монотонно возрастает; при
![]() убывает; при
убывает; при
![]() возрастает. В точке
имеет экстремум (минимум), причем
возрастает. В точке
имеет экстремум (минимум), причем
![]() .
.
Подчеркнем, что в точке не имеет экстремума, а имеет разрыв 2-го рода.
Пример 6.41.
Найти наибольшее и наименьшее значения
функции
![]() на отрезке
на отрезке
![]() .
.
Решение.
Заметим, что заданная функция
непрерывна на всей числовой оси, а,
значит, и на отрезке
.
Как известно, такая функция достигает
своего наибольшего и наименьшего
значений на отрезке
либо в критических точках, либо на концах
отрезка. Найдем критические точки из
условия
![]() .
.
![]() ,
откуда получим
,
откуда получим
![]() .
Корнями этого уравнения являются
.
Корнями этого уравнения являются
![]() ,
,
![]() - критические точки
.
Вычислим и сравним между собой значения
- критические точки
.
Вычислим и сравним между собой значения
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
на отрезке
достигает наибольшего значения, равного
![]() ,
в двух точках
и
,
в двух точках
и
![]() и достигает наименьшего значения,
равного
и достигает наименьшего значения,
равного
![]() ,
также в двух точках
и
,
также в двух точках
и
![]() .
.
Пример 6.42.
Найти интервалы выпуклости и точки
перегиба графика функции
![]() .
.
Решение.
Заданная функция определена и непрерывна
на всей числовой оси. Найдем ее вторую
производную
![]() :
:
![]() ,
,
![]()
К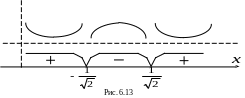 ритическими
точками 2-го рода, в которых
ритическими
точками 2-го рода, в которых
![]() ,
являются
,
являются
![]() ,
,
![]() .
Знаки
легко исследовать методом интервала.
На рис. 6.13 указан знак
.
Знаки
легко исследовать методом интервала.
На рис. 6.13 указан знак
![]() на каждом из интервалов ее знакопостоянства.
Там же указано направление выпуклости
графика
,
соответствующее этому знаку.
на каждом из интервалов ее знакопостоянства.
Там же указано направление выпуклости
графика
,
соответствующее этому знаку.
При
![]() график
выпуклый вниз; при
график
выпуклый вниз; при
![]() - выпуклый вверх; при
- выпуклый вверх; при
![]() - выпуклый вниз. Имеются две точки
перегиба графика:
- выпуклый вниз. Имеются две точки
перегиба графика:
![]() и
и
![]() ,
где
,
,
где
,
![]() ,
а ординаты
,
а ординаты
![]() ,
,
![]() находятся из соотношений:
находятся из соотношений:
![]() ;
;
![]() ,
,
т.е.
![]() ;
;
![]() .
.
Заметим, что график
симметричен относительно оси
![]() ,
поскольку эта функция четная, т.е.
,
поскольку эта функция четная, т.е.
![]() .
.
Пример 6.43.
Найти асимптоты графика функции
![]() .
.
Решение.
Вертикальной асимптотой является прямая
![]() ,
поскольку при
,
поскольку при
![]()
![]() .
Правую наклонную асимптоту
.
Правую наклонную асимптоту
![]() найдем из соотношений:
найдем из соотношений:
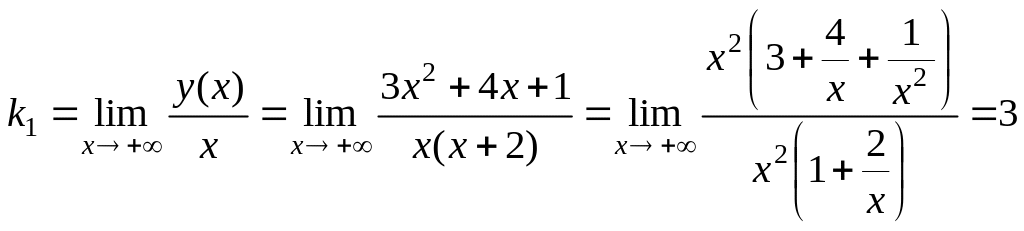 ,
,
![]() ,
,
таким образом,
![]() - правая наклонная асимптота.
- правая наклонная асимптота.
Левая наклонная асимптота
![]() находится аналогично:
находится аналогично:
![]() ,
,
![]() ,
т.е. правая наклонная асимптота является
одновременно и левой наклонной асимптотой.
,
т.е. правая наклонная асимптота является
одновременно и левой наклонной асимптотой.
Пример 6.44.
Провести полное исследование функции
![]() и построить ее график.
и построить ее график.
Решение.
Областью определения функции является множество
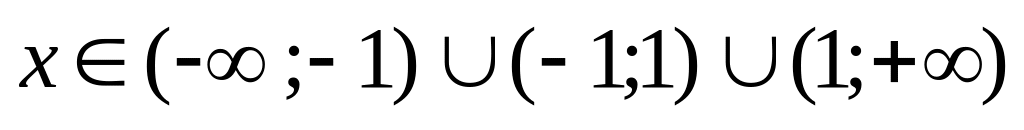 .
Функция является четной, т.е.
и ее график симметричен относительно
оси
.
Функция терпит разрыв 2-го рода в точках
.
Функция является четной, т.е.
и ее график симметричен относительно
оси
.
Функция терпит разрыв 2-го рода в точках
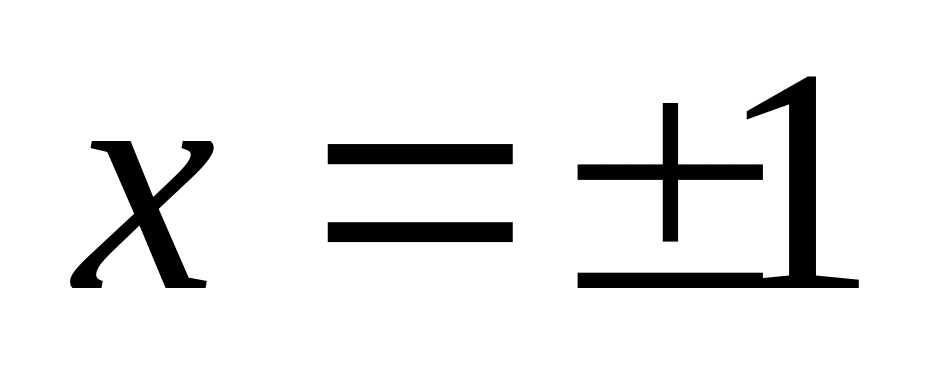 .
.Вертикальными асимптотами графика
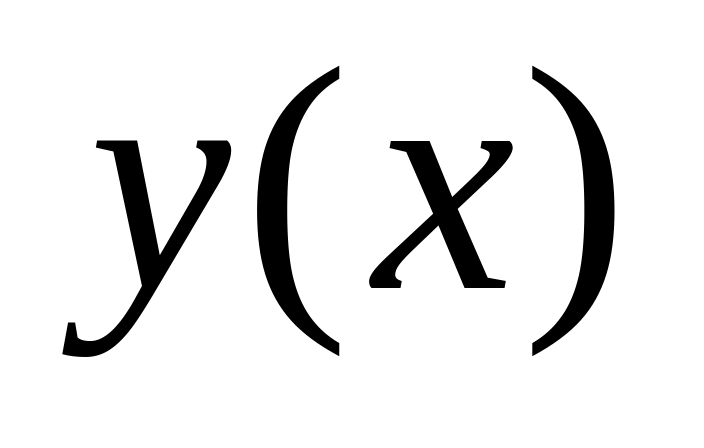 являются прямые
являются прямые
 и
и
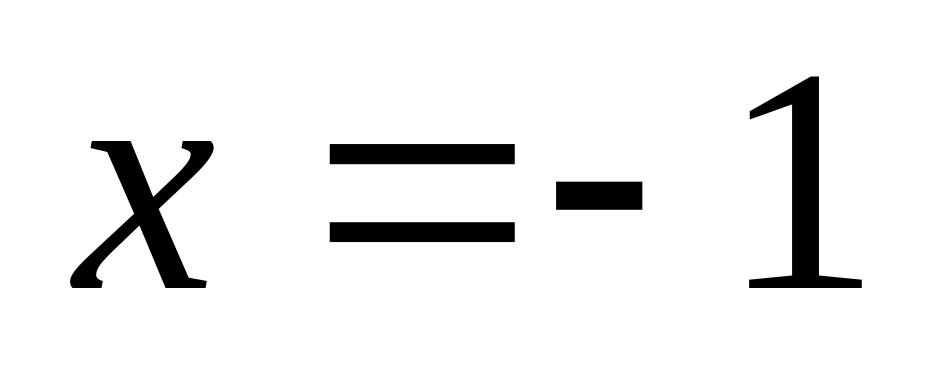 .
Правая наклонная асимптота
.
Правая наклонная асимптота
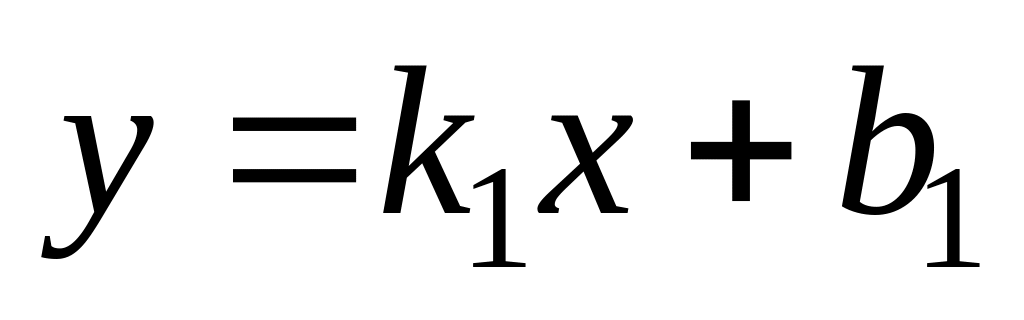 определяется из условий:
определяется из условий:
![]()
![]() ,
,
т.е. правой наклонной асимптотой
является горизонтальная прямая
![]() ,
которая в силу симметрии графика,
является также и левой наклонной
асимптотой.
,
которая в силу симметрии графика,
является также и левой наклонной
асимптотой.
Для исследования монотонности и экстремумов найдем :
![]()
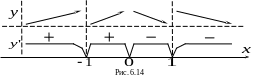 .
Знаки
.
Знаки
![]() и характер монотонности
на соответствующих интервалах указаны
на рис. 6.14.
и характер монотонности
на соответствующих интервалах указаны
на рис. 6.14.
Функция имеет экстремум (максимум) в точке , причем
![]() .
.
Для исследования направления выпуклости графика
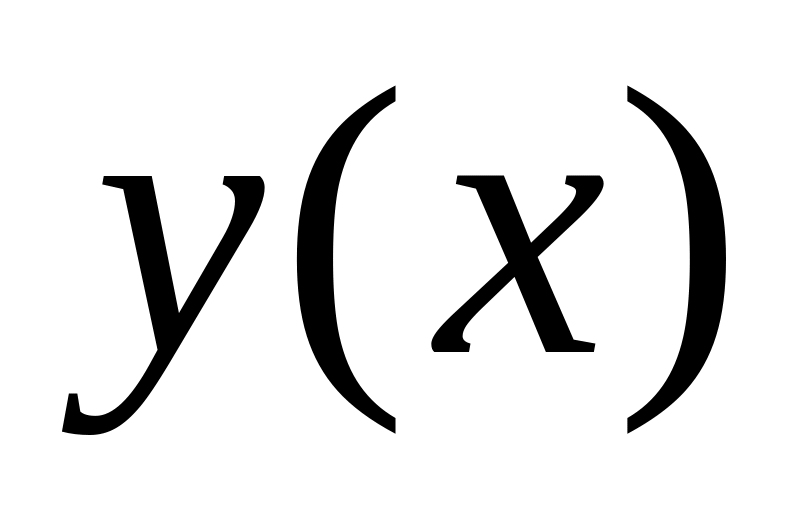 рассмотрим
:
рассмотрим
:
![]() .
.
Знаки и направление выпуклости графика на соответствующих интервалах указаны на рис. 6.15.
З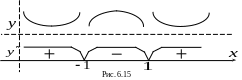
 аметим,
что точки перегиба графика отсутствуют,
поскольку при
аметим,
что точки перегиба графика отсутствуют,
поскольку при
![]() функция
не определена (имеет разрыв 2-го рода).
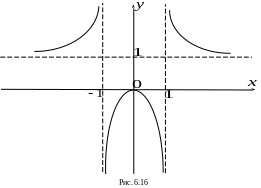
График
изображен на рис. 6.16.
функция
не определена (имеет разрыв 2-го рода).
График
изображен на рис. 6.16.
Пример 6.45.
Провести полное исследование функции
![]() и построить ее график.
и построить ее график.
Решение.
Областью определения функции является множество
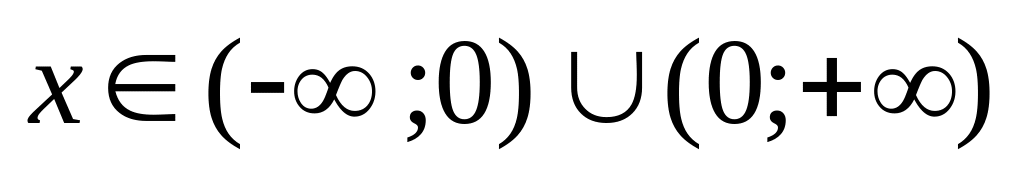 ;
функция является нечетной (
;
функция является нечетной (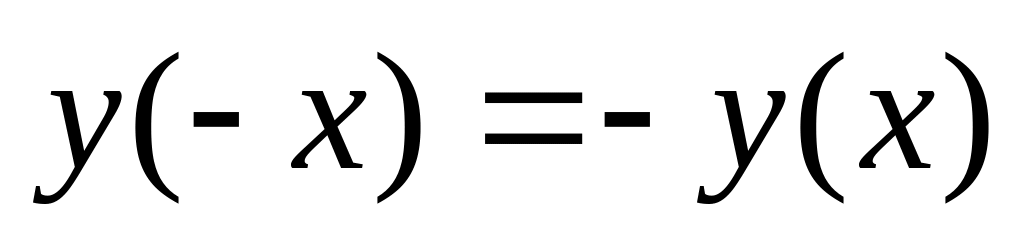 )
и терпит разрыв 2-го рода в точке
.
)
и терпит разрыв 2-го рода в точке
.Вертикальной асимптотой графика является ось
 .
Правая наклонная асимптота
определяется из условий:
.
Правая наклонная асимптота
определяется из условий:
![]() ,
,
![]() ,
,
т.е. правой наклонной асимптотой
является прямая
![]() .
Легко видеть, что эта прямая является
также и левой асимптотой (при
.
Легко видеть, что эта прямая является
также и левой асимптотой (при
![]() ).
).
Для исследования монотонности и экстремумов найдем . Проделав соответствующие выкладки, получим:
![]() при любом
при любом
![]() , т.е. при
, т.е. при
![]() монотонно
возрастает и при
монотонно
возрастает и при
![]() также монотонно возрастает. Ясно, что
экстремумы
отсутствуют.
также монотонно возрастает. Ясно, что
экстремумы
отсутствуют.
Для определения направления выпуклости графика рассмотрим :
![]() .
.
П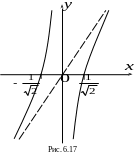 ри
ри
![]() выполняется неравенство
выполняется неравенство
![]() ,
т.е. график
выпуклый вверх; при
,
т.е. график
выпуклый вверх; при
![]() выполняется
выполняется
![]() ,
т.е. график
выпуклый вниз, при этом точки перегиба
отсутствуют, поскольку при
функция
не определена (имеет место разрыв 2-го
рода).
,
т.е. график
выпуклый вниз, при этом точки перегиба
отсутствуют, поскольку при
функция
не определена (имеет место разрыв 2-го
рода).
Точки пересечения графика с осью
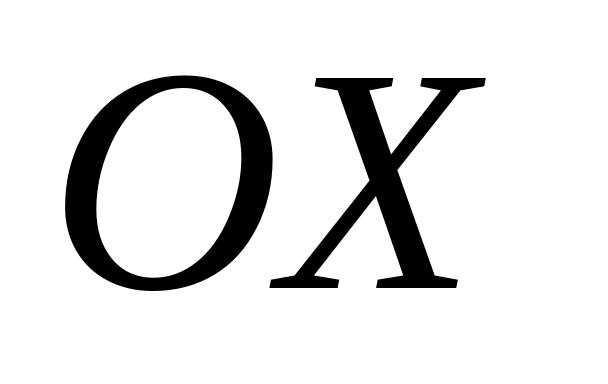 найдем из соотношения
найдем из соотношения
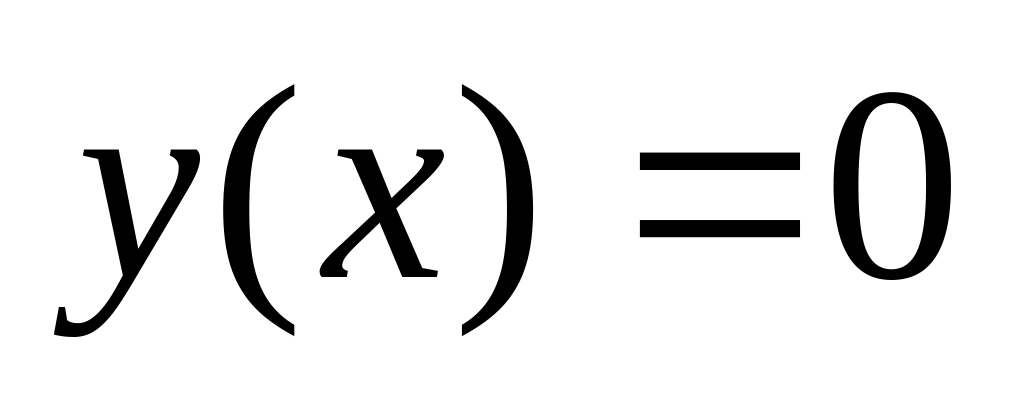 ,
т.е.
,
т.е.
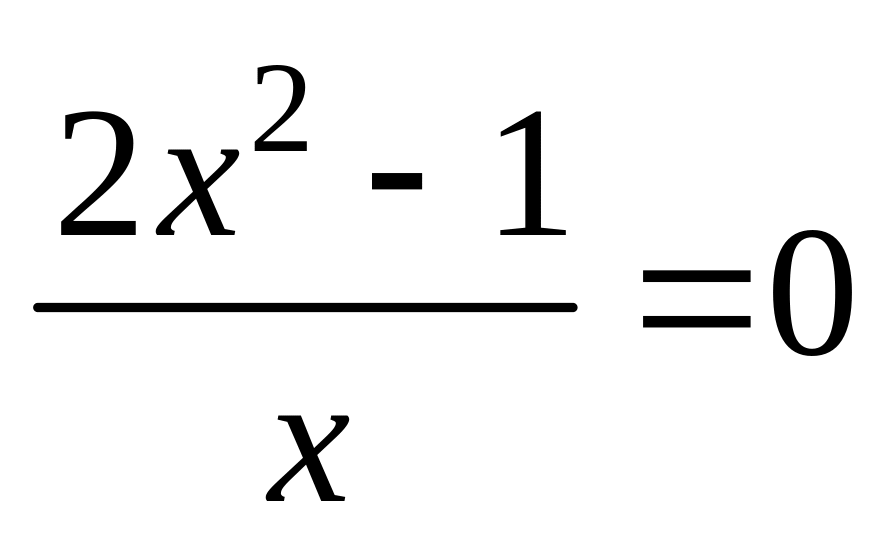 ,
откуда
,
откуда
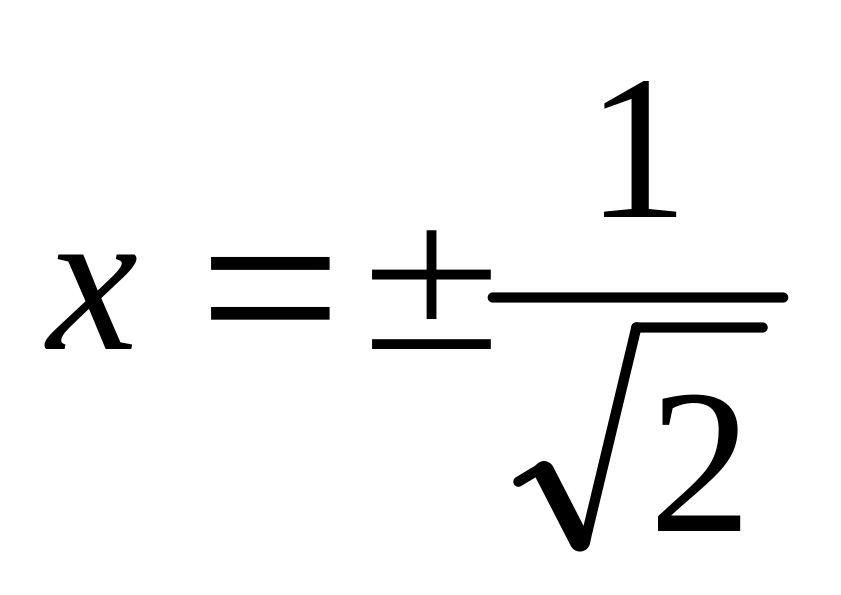 .
График
изображен на рис. 6.17.
.
График
изображен на рис. 6.17.
