6.4. Исследование функции на непрерывность

В задании требуется найти все точки разрыва функции (если они есть), указать их тип и построить эскиз графика функции в окрестности каждой из этих точек. Кроме примеров данного раздела см. также примеры 3.1-3.7.

Пример 6.27. Исследовать на непрерывность функцию .

Решение. Заданная элементарная функция определена на множестве , таким образом, она заведомо непрерывна во всех точках этого множества, а ее точкой разрыва является .

Поскольку ; , то в точке заданная функция имеет разрыв 2-го рода (бесконечный разрыв). Эскиз графика в окрестности точки представлен на рис. 6.8.

П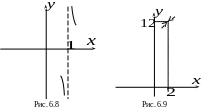 ример 6.28. Исследовать на непрерывность функцию .

Решение. Область определения заданной элементарной функции представляет собой множество , а значит, она непрерывна во всех точках этого множества и имеет точку разрыва . Выполняются равенства: , но при этом не существует, поэтому в точке заданная функция имеет разрыв 1-го рода, причем устранимый (эскиз графика в окрестности точки изображен на рис. 6.9).

З аметим, что если доопределить заданную функцию в точке , приняв , то соответствующая новая функция будет непрерывной всюду на числовой оси.

Пример 6.29. Исследовать на непрерывность .

Решение. Согласно определению модуля, получим если и если , поэтому заданную функцию можно записать так:

в точке же не определена.

При является непрерывной, т.к. – непрерывная функция, при также непрерывна.

Х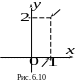 арактер разрыва в точке установим, вычислив, соответствующий правый и левый пределы:

,

.

Оба они существуют (при этом различны), поэтому в точке имеет разрыв 1-го рода, не являющийся устранимым. Эскиз графика в окрестности точки разрыва изображен на рис. 6.10.

Пример 6.30. Исследовать на непрерывность .

Решение. Заданная элементарная функция определена на числовой прямой всюду, кроме точек, в которых ее знаменатель обращается в ноль, т.е. , , . Таким образом, точками разрыва заведомо являются …

Установим характер разрыва при . Поскольку при , то 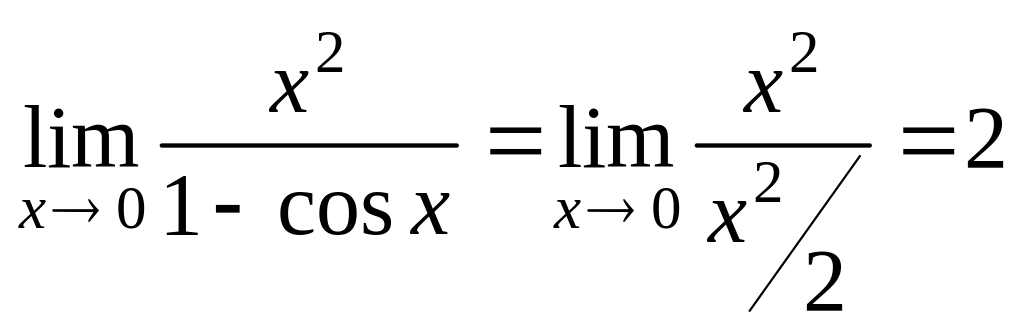, т.е. - точка разрыва первого рода, причем устранимого.

Установим характер разрыва при , … Поскольку , причем для , то

, .

Итак, имеет бесконечное множество точек разрыва 2-го рода , … и одну точку устранимого разрыва 1-го рода ; эскиз графика в окрестностях этих точек изображен на рис. 6.11

П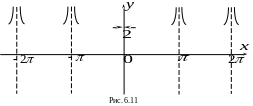 ример 6.31. Исследовать на непрерывность

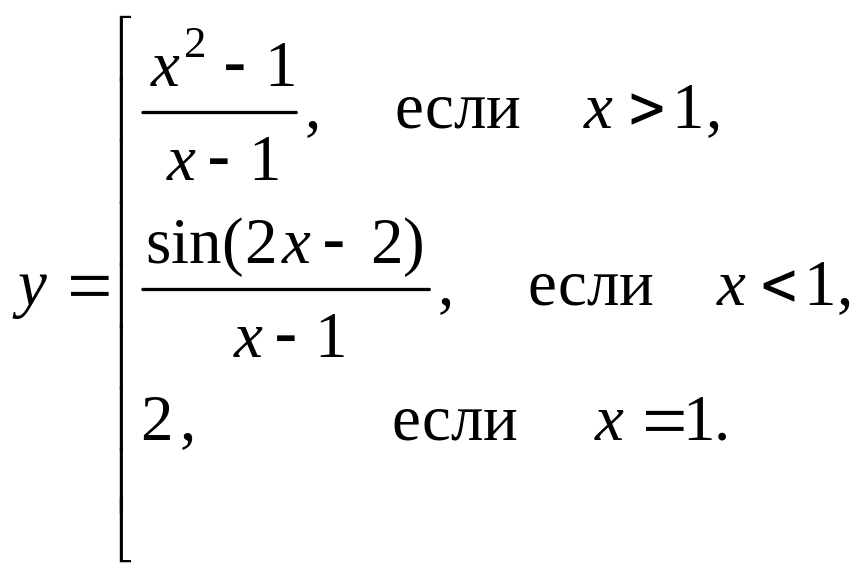
Решение. Функция определена на всей числовой прямой, причем она заведомо непрерывна в любой точке . Посмотрим, есть ли разрыв в точке .

,

.

Здесь учтено, что при , т.е. при . По условию задачи , поэтому можно записать, что и, следовательно, непрерывна в точке (а, значит, и на всей числовой оси).

6.5. Найти производные функций

Кроме примеров данного раздела см. также примеры 4.4, 4.6 – 4.9.

Пример 6.32. Найти первую и вторую производные функции .

Решение. Заметим, что данная функция является сложной, причем можно записать: . Далее, используя известное свойство логарифма, преобразуем функцию к виду , после чего, согласно правилу дифференцирования сложной функции, получим:

.

Следует заметить, что если не использовать вышеуказанное свойство логарифма, то выкладки будут несколько длиннее:

.

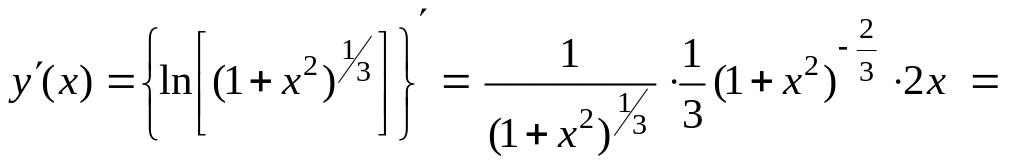
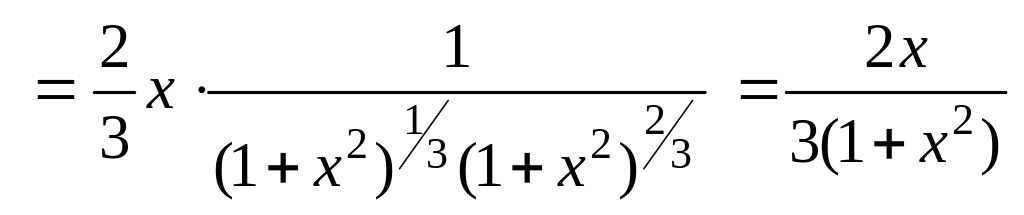Вычислим вторую производную:

Пример 6.33. Найти производную функции, заданной параметрически: - константы.

Решение.

Пример 6.34. Найти производную функции, заданной неявно: .

Решение. Перепишем заданное соотношение в виде Далее приравняем нулю производную по левой части этого соотношения, вычисленную как производную сложной функции:

; ;

.

Из последнего уравнения выразим через и :

; ;