6.2. Задачи на вычисление предела последовательности
Пример 6.8.
(неопределенность вида
).
Решение.
=
=
=
.
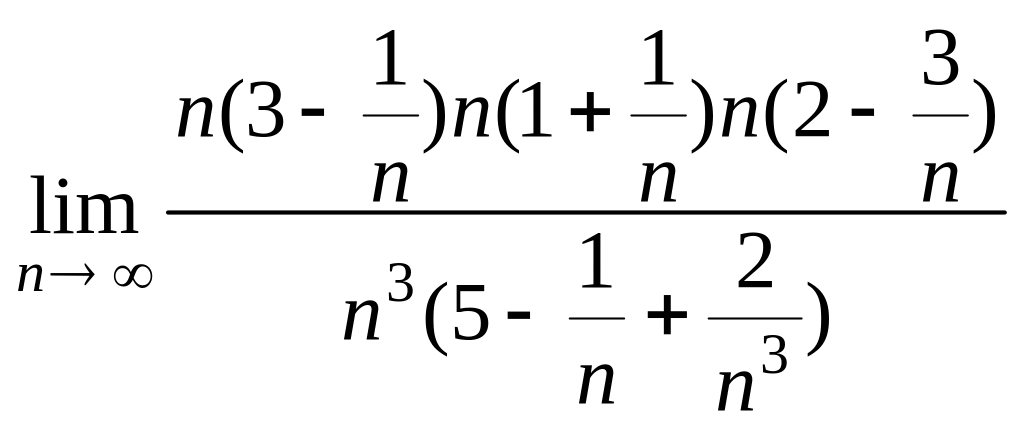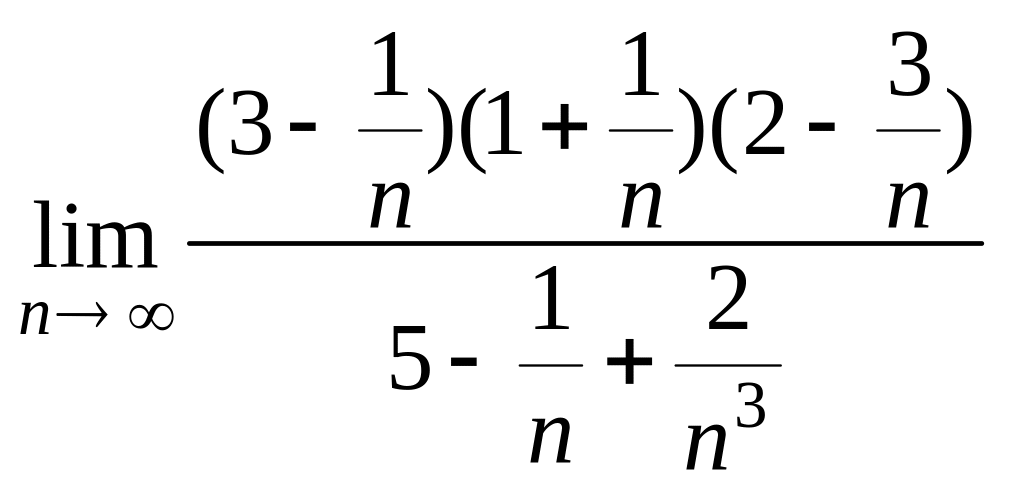
Пример 6.9.
(неопределенность вида
).
Решение.
=
.
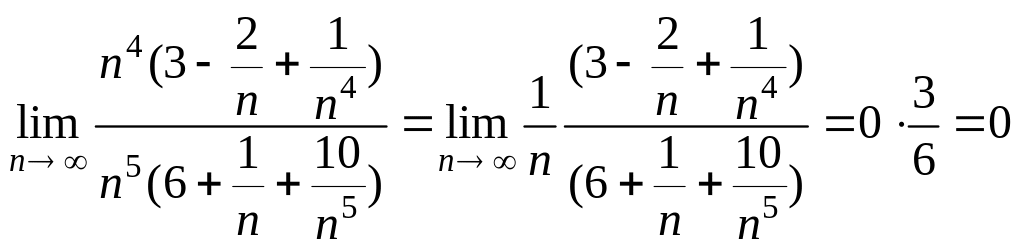Пример 6.10.
(неопределенность вида
).
Решение.
=
.
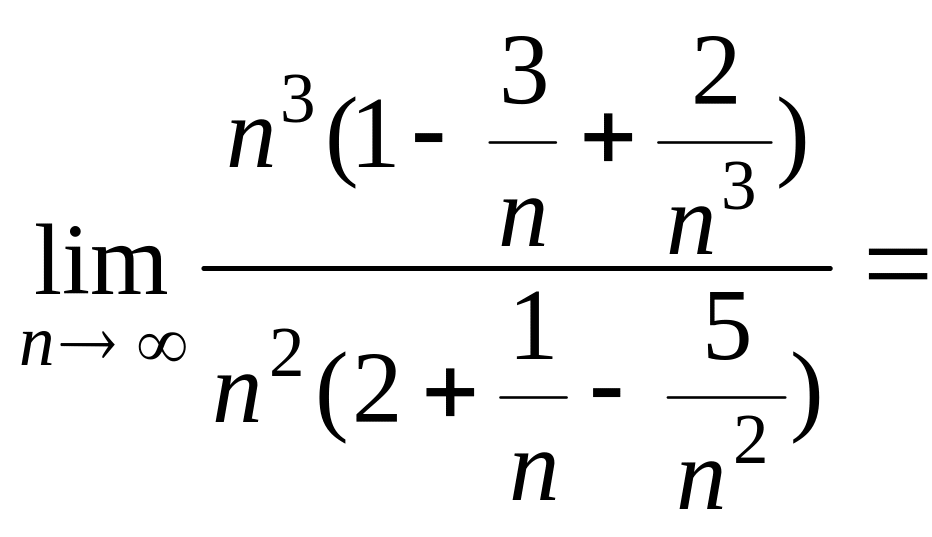
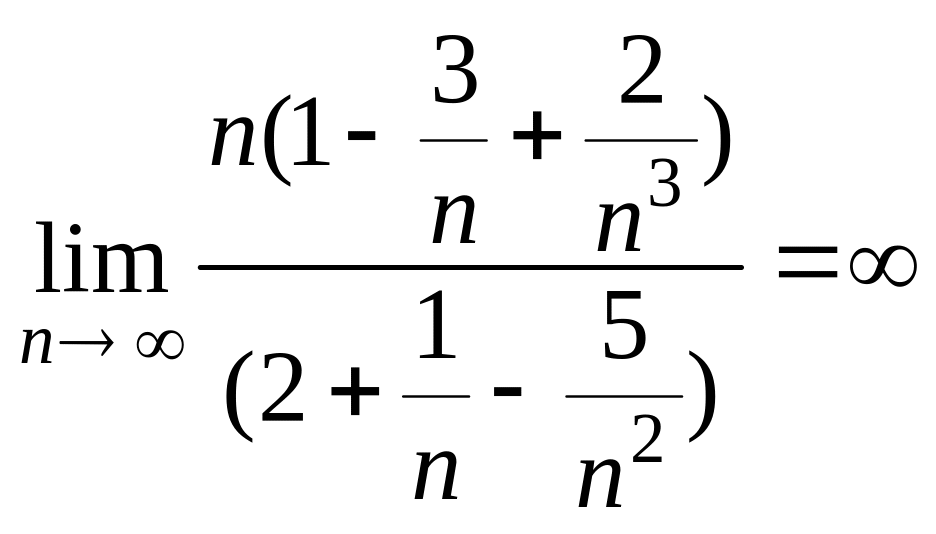Последнее, достаточно очевидное
равенство можно строго обосновать,
например, таким образом.
Обозначим
,
.
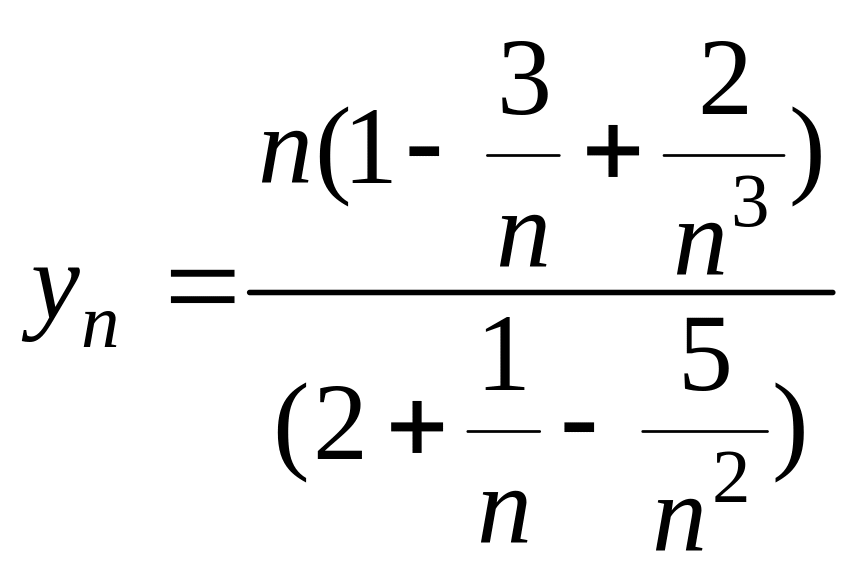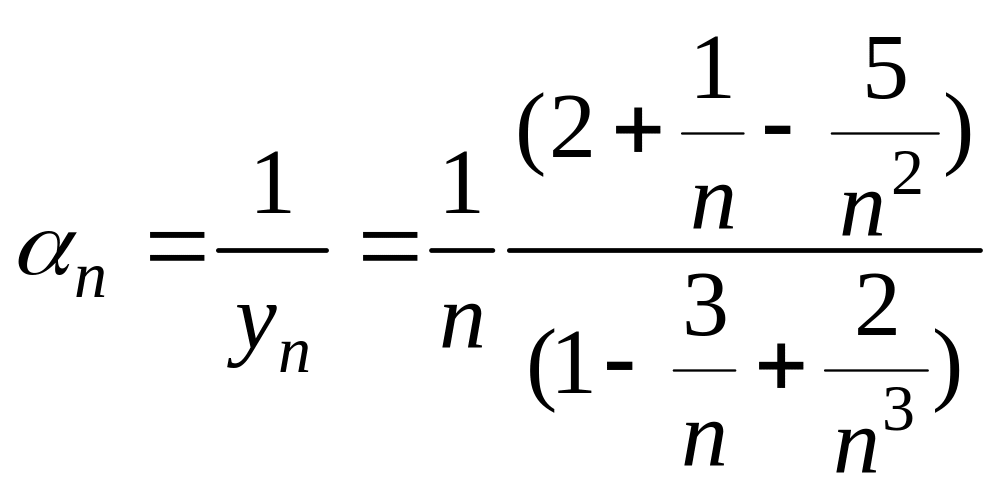Поскольку
,
то по свойству бесконечно малых и
бесконечно больших величин получим
.
Пример 6.11.
(неопределенность вида
).
Решение:
=
.
Здесь учтено, что
.
Пример 6.12.
(неопределенность вида
).
Решение.
.
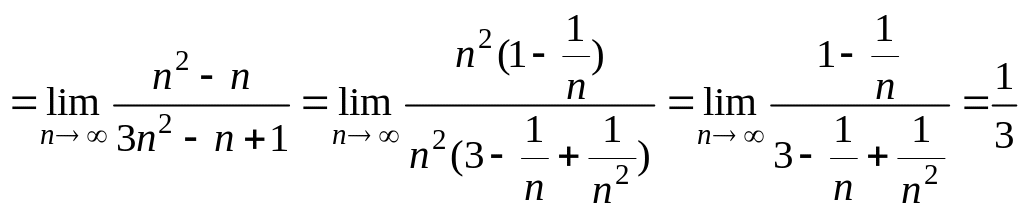Пример 6.13.
(неопределенность вида
).
Решение.
=
=
,
поскольку
.
Пример 6.14.
Решение:
Заметим, что последовательность
,
соответствующая выражению в числителе,
является ограниченной, поскольку при
всех
заведомо выполняется неравенство
,
откуда
.
Последовательность же
является бесконечно малой, так как
.
В результате, согласно известному
свойству, последовательность
также является бесконечно малой, т.е.
= 0.
Пример 6.15.
(неопределенность вида
).
Решение. Предлагаемую неопределенность раскроем с помощью второго замечательного предела:
=
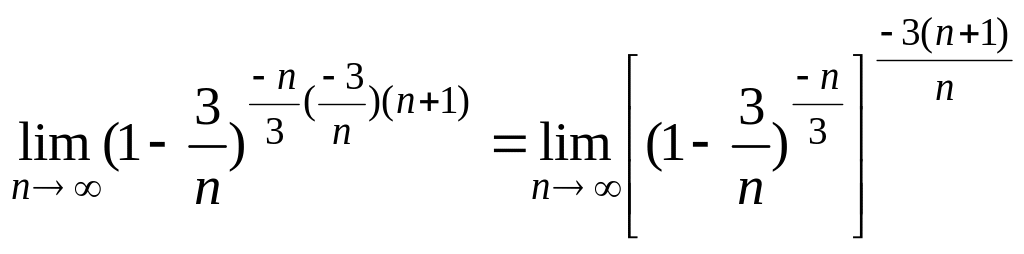
Рассмотрим
,
где
- бесконечно малая последовательность,
т.к.
.
Кроме того,
,
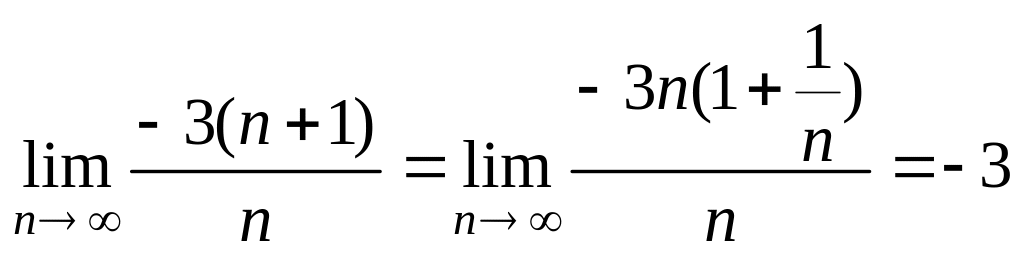в результате
.
Изложим еще один вариант решения данной задачи:
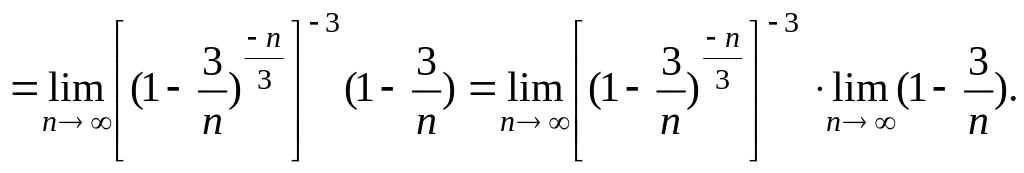
Поскольку
,
то, опять же учитывая второй замечательный
предел, получим, что искомый предел
равен
.
Пример 6.16.
(неопределенность вида
).
Решение. Заметим,
что
,
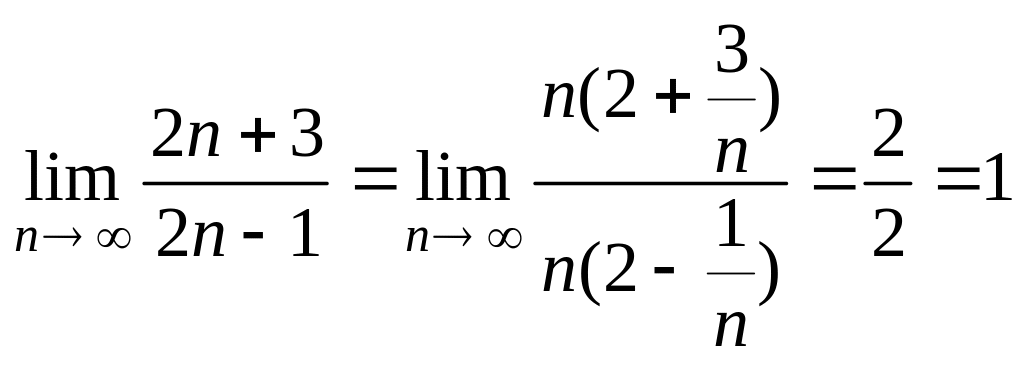поэтому действительно имеет место
неопределенность вида
.
Представим выражение
в виде
.
Задача свелась к аналогичной той, что рассмотрена в примере 6.15:
=
.
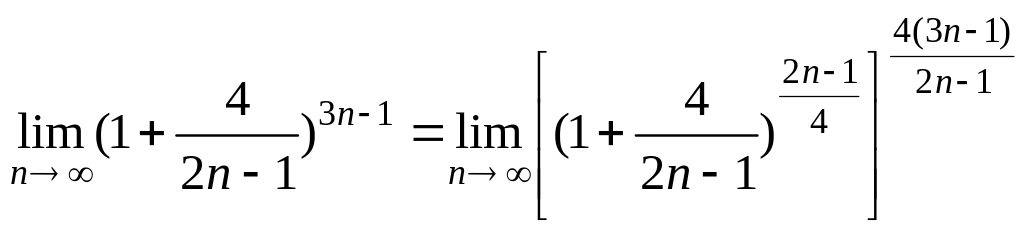Поскольку
,
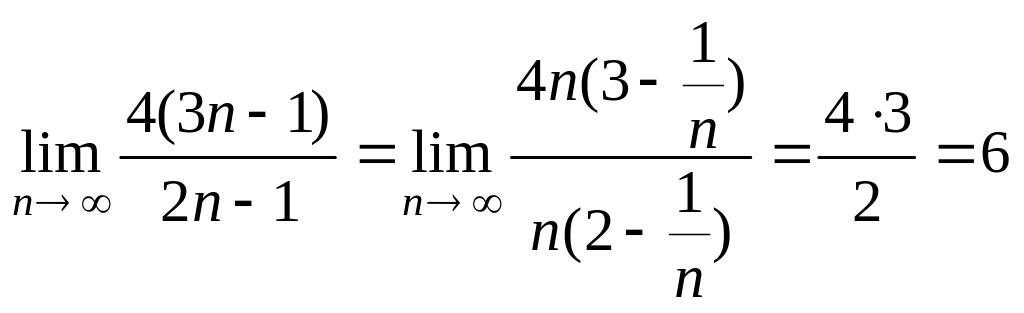то искомый предел равен
.
6.3. Задачи на вычисление предела функции
Кроме нижеследующих примеров см. также примеры 2.13-2.18 и 2.24.
При вычислении
пределов часто приходится пользоваться
следующей таблицей эквивалентности
бесконечно малых функций (при
):
; 
; 
;
; 
; 
;
; 
,
где
– константа ;
;
,
где
(любая константа).
Пример 6.17.
(неопределенность вида
).
Решение.
Разложим числитель и знаменатель на
простые множители. Поскольку корнями
уравнения
являются
и
,
то
.
Пример 6.18.
.
Решение.
Заметим, что при
числитель заданного выражения стремится
к значению
,
а знаменатель – к нулю, поэтому искомый
предел равен бесконечности. Строгое
обоснование этого утверждения может
быть, например, таким. Поскольку при
функция
является бесконечно малой, то заданная
функция
является бесконечно большой.
Пример 6.19.
(неопределенность вида
).
Решение.
.
Пример 6.20.
(неопределенность вида
).
Решение.
Пример 6.21.
(неопределенность вида
).
Решение.
Поскольку при
,
,
то
.
Пример 6.22.
(неопределенность вида
).
Решение.
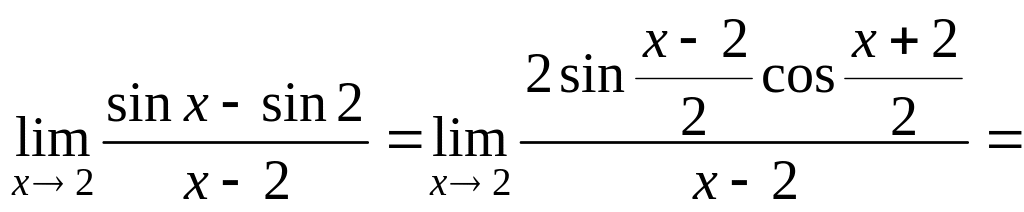
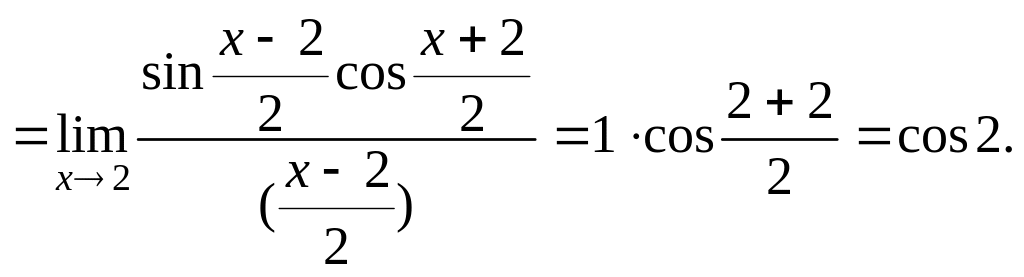
Здесь
использовано то, что при
и при этом
(первый замечательный предел).
Пример 6.23.
(неопределенность вида
).
Решение.
Заметим, что при
сумма бесконечно малых, стоящая в
числителе, эквивалентна
(бесконечно малой самого низкого
порядка), а сумма бесконечно малых в
знаменателе – функции
,
при этом
.
Таким образом, искомый предел равен:
.
Пример 6.24.
(неопределенность вида
).
Решение.
Введем новую переменную
,
тогда
Поскольку при
,
т.е. при
,
то
.
Пример 6.25.
(особенность вида
).
Решение.
.
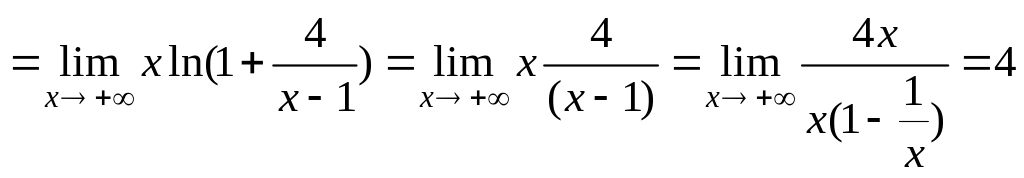Здесь было использовано соотношение эквивалентности бесконечно малых
при
,
поскольку при этом
.
Пример 6.26.
(особенность вида
).
Решение.
Заметим, что
(здесь обозначено
),
кроме того, учитывая первый замечательный
предел, получим
.
В результате искомый предел равен
.