
- •Содержание
- •Глава 1 понятие функции
- •1.1. Понятие функции, способы её задания. Последовательность
- •Различают три основных способа задания функции.
- •1 .2. Основные элементарные функции
- •Глава 2 предел функции
- •2.1. Предел функции, односторонний предел. Предел последовательности.
- •2.2. Понятия бесконечно малой и бесконечно большой функций. Ограниченная функция.
- •Свойство бесконечно малых и бесконечно больших функций.
- •2.3. Основные теоремы о пределах. Первый и второй замечательные пределы. Сравнение бесконечно малых.
- •Сравнение бесконечно малых.
- •Глава 3 непрерывность функции
- •3.1. Непрерывность функции в точке. Разрывная функция. Классификация точек разрыва.
- •3.2. Теоремы о непрерывных функциях
- •3.3. Свойства функций, непрерывных на отрезке.
- •Глава 4 производная
- •4 .1. Понятие производной, её физический и геометрический смысл. Дифференциал функции.
- •4.2. Правила дифференцирования. Производные основных элементарных функций. Производная обратной функции.
- •4.3. Производная функции, заданной параметрически. Производная неявной функции. Производные высших порядков.
- •4.4. Теоремы о дифференцируемых функциях. Правило Лопиталя.
- •Глава 5 исследование поведения функций.
- •5.1. Возрастание и убывание функций.
- •5.2. Экстремумы функций. Наибольшее и наименьшее значения функции на отрезке.
- •5.3. Выпуклость графика функции. Точки перегиба.
- •5.4. Асимптоты графика функции. Общее исследование функций и построение графиков.
- •Глава 6 рекомендуемые задачи
- •6.1. Построение графиков функций без применения методов дифференциального исчисления
- •6.2. Задачи на вычисление предела последовательности
- •6.3. Задачи на вычисление предела функции
- •6.4. Исследование функции на непрерывность
- •6.5. Найти производные функций
- •6.6. Задачи на вычисление пределов функций с использованием правила Лопиталя
- •6.7. Исследование поведения функций с помощью производных
- •Глава 7 варианты расчетно-графических работ
- •7.1. Построить графики функций без применения методов дифференциального исчисления
- •7.2. Вычислить предел последовательности
- •7.3. Вычислить предел функции
- •7.4. Исследовать функцию на непрерывность
- •7.5. Найти производные функций
- •7.6. Вычислить предел функции с использованием правила Лопиталя
- •7.7. Исследовать поведение функции с помощью методов дифференциального исчисления
- •Литература
- •Для заметок
Глава 6 рекомендуемые задачи
6.1. Построение графиков функций без применения методов дифференциального исчисления
Рассмотрим
случаи, когда построение графика функции
легко осуществить без ее полного
исследования методами дифференциального
исчисления. При этом будем использовать
графики основных элементарных функций,
а также применять некоторые известные
правила. Пусть кривая
![]() является графиком функции
является графиком функции
![]() .
Тогда графики нижеперечисленных функций
получаются из
при помощи следующих операций (
.
Тогда графики нижеперечисленных функций
получаются из
при помощи следующих операций (![]() - константа):
- константа):
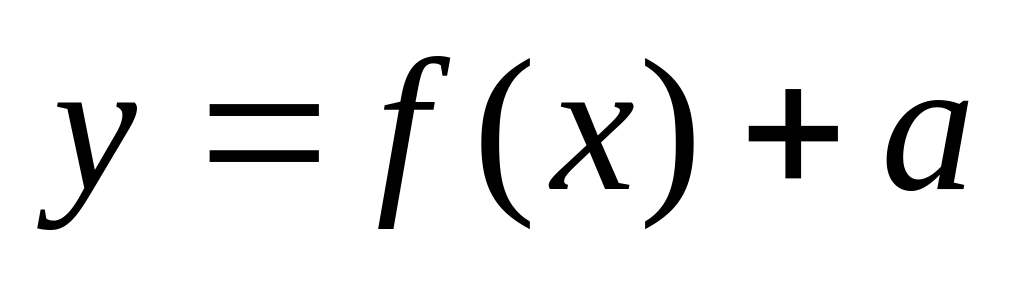 - параллельный перенос
вдоль оси OY на величину
.
- параллельный перенос
вдоль оси OY на величину
.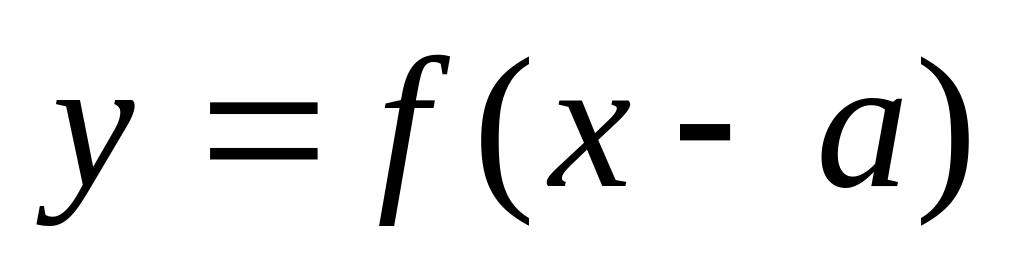 - параллельный перенос
вдоль оси OX на величину
.
- параллельный перенос
вдоль оси OX на величину
.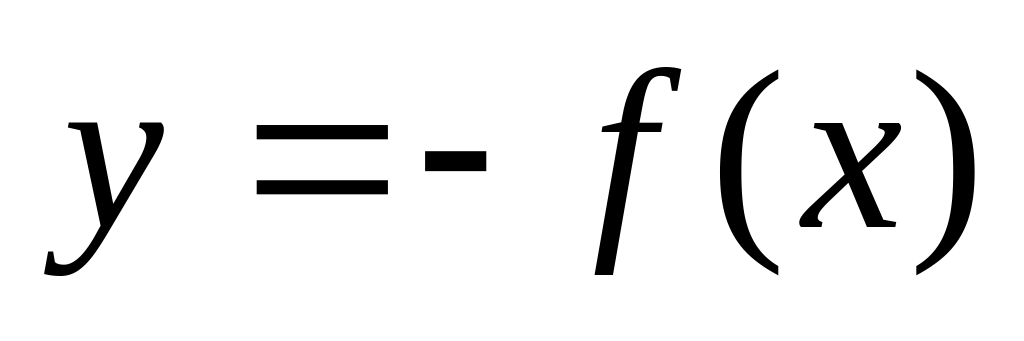 - зеркальное отображение
относительно оси OX.
- зеркальное отображение
относительно оси OX.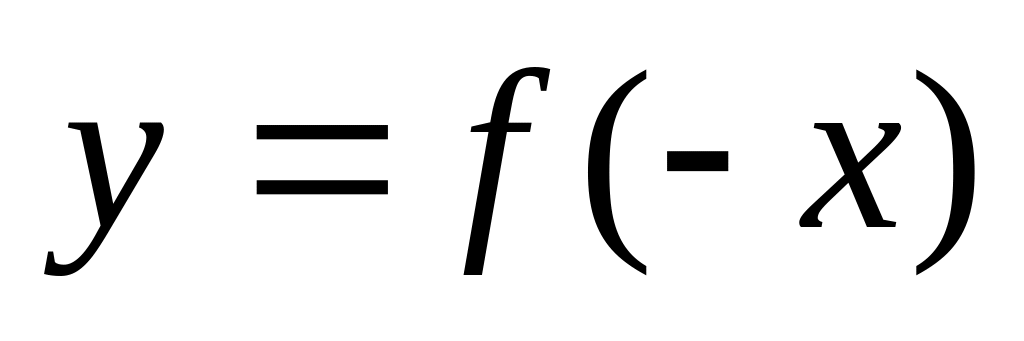 - зеркальное отображение
относительно оси OY.
- зеркальное отображение
относительно оси OY. - при
- при
 – сжатие вдоль оси OY в
– сжатие вдоль оси OY в
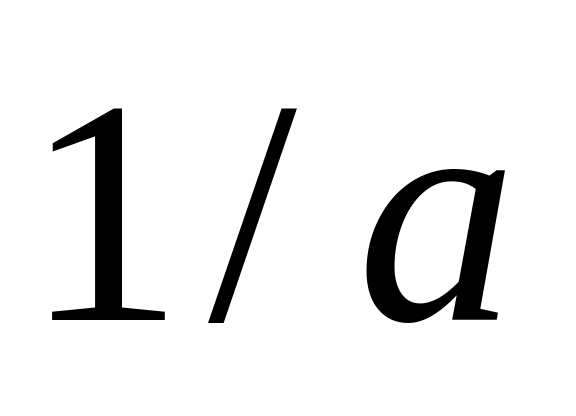 раз; при
раз; при
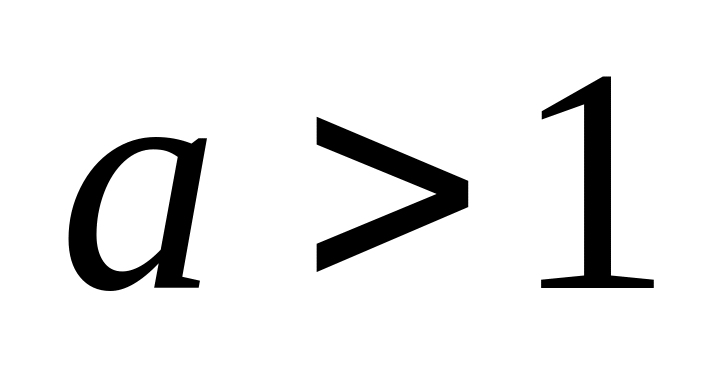 – растяжение вдоль оси OY
в
раз.
– растяжение вдоль оси OY
в
раз. - при
– растяжение вдоль оси OX
в
раз; при
– сжатие вдоль оси OX в
раз.
- при
– растяжение вдоль оси OX
в
раз; при
– сжатие вдоль оси OX в
раз.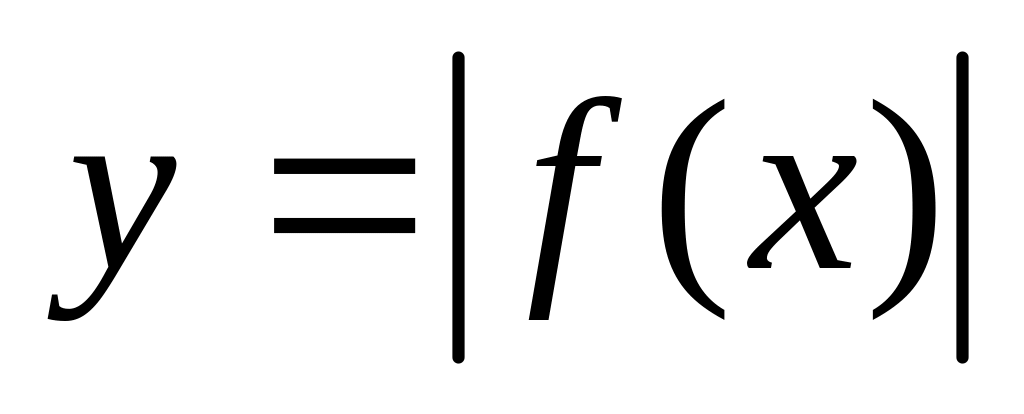 - кривая
остается без изменения на участках,
где
- кривая
остается без изменения на участках,
где
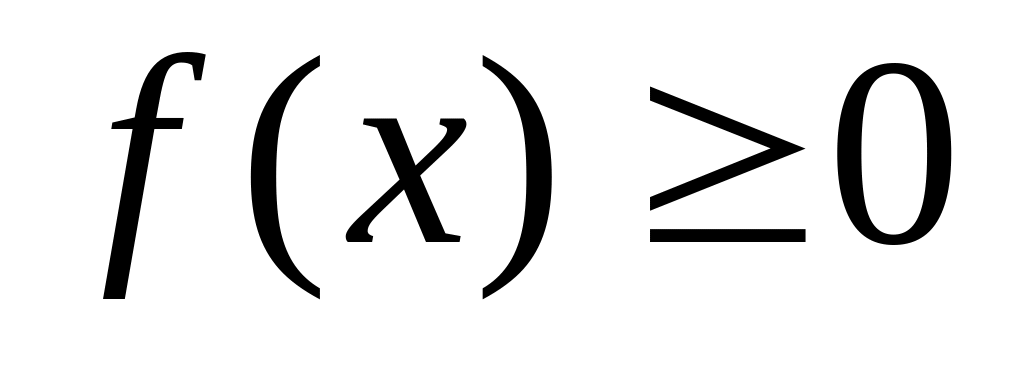 и зеркально отображается относительно
оси OX на участках, где
и зеркально отображается относительно
оси OX на участках, где
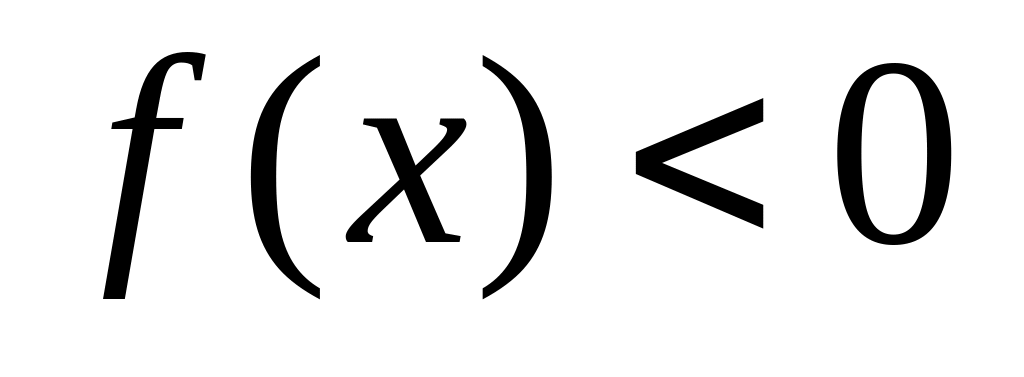 .
. - график совпадает с кривой
при
- график совпадает с кривой
при
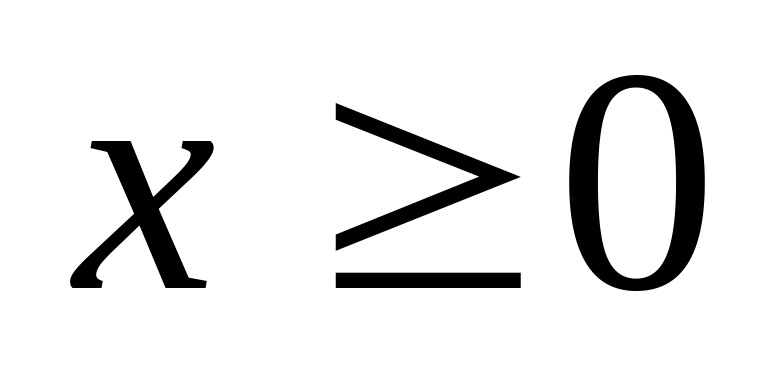 и при этом симметричен относительно
оси OY.
и при этом симметричен относительно
оси OY.
Пример 6.1.
Построить график функции
![]() .
.
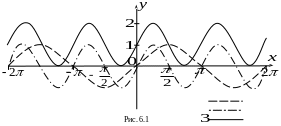
Решение. Процесс построения осуществим в три этапа (рис. 6.1):
кривая
1 – график функции
![]() ;
;
кривая
2 – график функции
![]() – строится путем сжатия кривой 1 вдоль
оси
OX
в два раза;
– строится путем сжатия кривой 1 вдоль
оси
OX
в два раза;
кривая
3 – график заданной функции
![]() – строится путем сдвига кривой 2 на
единицу вверх вдоль оси OY.
– строится путем сдвига кривой 2 на
единицу вверх вдоль оси OY.
 Пример
6.2. Построить график функции
Пример
6.2. Построить график функции
![]() .
.
 Решение.
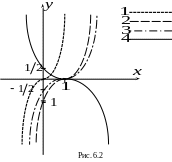
Строим последовательно графики функций
(рис.6.2):
Решение.
Строим последовательно графики функций
(рис.6.2):
кривая 1 - график
![]() ;
;
кривая 2 - график
![]() –
путем сдвига кривой 1 вправо на единицу
вдоль оси OX;
–
путем сдвига кривой 1 вправо на единицу
вдоль оси OX;
кривая 3 - график
![]() – путем сжатия кривой 2 вдоль оси OY
в два раза;
– путем сжатия кривой 2 вдоль оси OY
в два раза;
кривая 4 - график
![]() – зеркальное отображение кривой 3
относительно оси OX.
– зеркальное отображение кривой 3
относительно оси OX.
Пример 6.3.
Построить график дробно-линейной
функции
![]() .
.
Решение. Приведем один из возможных вариантов построения графика; для этого проведем преобразования:
![]() , т.е.
, т.е. ![]() .
.
С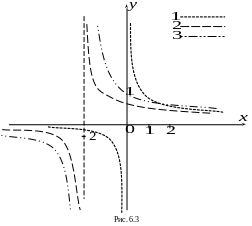 троим
последовательно графики (рис.6.3, 6.3а):
троим
последовательно графики (рис.6.3, 6.3а):
кривая 1 - график
![]() ;
;
кривая 2 - график
![]() - сдвиг кривой 1 вдоль оси OX на –2;
- сдвиг кривой 1 вдоль оси OX на –2;
к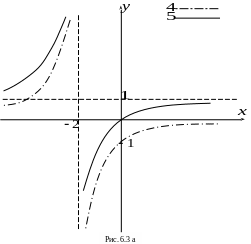 ривая
3 - график
ривая
3 - график
![]() - растяжение кривой 2 вдоль оси OY в 2 раза;
- растяжение кривой 2 вдоль оси OY в 2 раза;
кривая 4 - график
![]() - зеркальное отображение кривой 3
относительно оси OX;
- зеркальное отображение кривой 3
относительно оси OX;
кривая 5 - график
![]() - сдвиг кривой 4 вдоль оси OY на 1 вверх.
- сдвиг кривой 4 вдоль оси OY на 1 вверх.
Заметим, что график данной функции можно также легко построить, опираясь на известные свойства дробно-линейной функции (наличие вертикальной и горизонтальной асимптот) и определяя координаты точек пересечения графика с осями координат.
П ример
6.4. Построить график функции
ример
6.4. Построить график функции
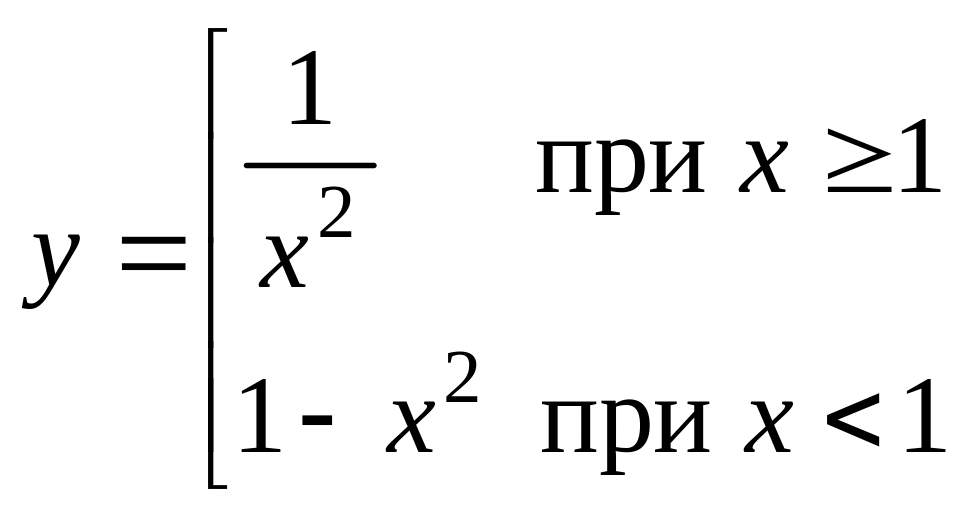
Решение.
Для
![]() строим график
строим график
![]() путем последовательного построения
графиков функций
путем последовательного построения
графиков функций
![]() применяя операции зеркального отображения
относительно оси OX и
сдвига на 1 вверх вдоль о
применяя операции зеркального отображения
относительно оси OX и
сдвига на 1 вверх вдоль о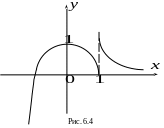 си
OY. Для
си
OY. Для
![]() строим график
строим график
![]() .
.
Пример 6.5.
Построить график функции
![]() .
.
Р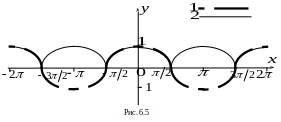 ешение.
Построим сначала график
ешение.
Построим сначала график
![]() ;
на рис. 6.5 ему соответствует штрих -
пунктирная кривая 1. Графику
;
на рис. 6.5 ему соответствует штрих -
пунктирная кривая 1. Графику
![]() на рис. 6.5 соответствует кривая 2 (сплошная
линия). Она совпадает с кривой 1 на
участках, где
на рис. 6.5 соответствует кривая 2 (сплошная
линия). Она совпадает с кривой 1 на
участках, где
![]() и является зеркальным отображением
кривой 1 относительно оси OX
на участках, где
и является зеркальным отображением
кривой 1 относительно оси OX
на участках, где
![]() .
.
Пример 6.6.
Построить график функции
![]() .
.
Р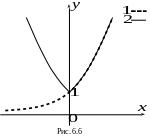 ешение.
Построим график
ешение.
Построим график
![]() (кривая 1 рис. 6.6). График
(кривая 2) совпадает с кривой 1 при
(кривая 1 рис. 6.6). График
(кривая 2) совпадает с кривой 1 при
![]() ,
и при этом симметричен относительно
оси OY.
,
и при этом симметричен относительно
оси OY.
Пример
6.7. Построить график функции
![]()
Решение: Используя свойство модуля, запишем:
при
![]() при
при
![]() .
.
И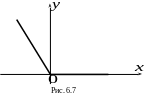 так,
так,
![]() График изображен на рис 6. 7.
График изображен на рис 6. 7.
