5.3. Выпуклость графика функции. Точки перегиба.

Определение. График дифференцируемой на функции называется выпуклым вверх (выпуклым вниз) на , если он расположен ниже (выше) своей касательной, проведенной в любой своей точке , (рис.5.3)

Ч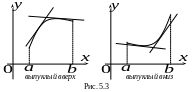 асто вместо термина «выпуклый вверх» употребляют термин «вогнутый вниз», а вместо «выпуклый вниз» – «вогнутый вверх».

Теорема. (достаточный признак характера выпуклости).

Пусть функция имеет на вторую производную.

Если при любом

, (5.3)

то график этой функции является на выпуклым вверх (вниз).

Определение. Точка графика непрерывной функции , которая отделяет его выпуклую вверх часть от выпуклой вниз, называется точкой перегиба.

Определение. Точка , в которой вторая производная функции обращается в ноль или терпит разрыв (при этом не существует), называется критической точкой второго рода.

Теорема. (необходимые условия существования точки перегиба). Если  точка перегиба графика непрерывной на функции , то абсцисса является критической точкой второго рода.

Теорема. (достаточные условия существования точки перегиба, или её отсутствия). Пусть существует окрестность , критической точки второго рода, в которой функция всюду непрерывна и имеет вторую производную везде, кроме, возможно, самой точки . Пусть при этом в интервалах и вторая производная сохраняет постоянные знаки. Если эти знаки противоположные, то точка графика функции с абсциссой является точкой перегиба, если же эти знаки одинаковые, то указанная точка точкой перегиба не является.

Пример 5.7. . Найдём , . Функция всюду дифференцируема, точка  единственная критическая точка второго рода: . Поскольку при и при , то  абсцисса точки перегиба. Её ординатой будет , т.е.  точка перегиба, причём для график выпуклый вверх, для  выпуклый вниз.

Пример 5.8. . Функция всюду непрерывна.

Найдём , , откуда видно, что  критическая точка второго рода, т.к. не существует. Поскольку для и для , то  точка перегиба, причём для график выпуклый вниз, а для  выпуклый вверх.

5.4. Асимптоты графика функции. Общее исследование функций и построение графиков.

Определение. Пусть точка перемещается по графику функции , неограниченно удаляясь от начала координат. Если при этом расстояние от этой точки до некоторой прямой стремится к нулю, то такая прямая называется асимптотой графика функции .

А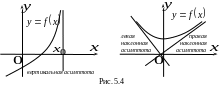 симптота может быть параллельной оси и тогда она называется вертикальной, или не параллельной ей и тогда она называется наклонной.

Теорема. (о вертикальных асимптотах).

Если существует такое число , что

, (5.4)

то прямая является вертикальной асимптотой графика функции . И обратно: если  вертикальная асимптота, то выполняется (5.4).

Пример 5.9. ; вертикальная асимптота – ось .

Теорема. (о наклонных асимптотах). Если для функции существуют пределы:

; , (5.5)

то прямая является правой наклонной асимптотой, т.е. асимптотой при .

Если существуют пределы:

; , (5.6)

то прямая является левой наклонной асимптотой, т.е. асимптотой при .

Важно подчеркнуть, что если график функции имеет правую (левую) асимптоту, то она единственная. Вертикальных же асимптот может быть даже бесконечно много, так, например, для графика функции асимптотами являются вертикальные прямые .

Пример 5.10. . Вертикальной асимптотой будет ось , т.к. при .

Наклонные асимптоты найдём из соотношений (5.5), (5.6):

,

, т.е. правая наклонная асимптота: , она же будет и левой наклонной асимптотой, т.к. при значения соответствующих пределов не изменятся.

Пример 5.11. , . Вертикальной асимптотой будет ось , т.к. при . Ищем наклонную асимптоту:

, т.е. наклонной асимптоты нет.

При общем исследовании функции и построении её графика рекомендуется следующий порядок действий.

1. Найдите её область определения, точки разрыва и интервалы непрерывности.

2. Найдите асимптоты графика функции.

3. Найдите интервалы возрастания и убывания функции.

4. Найдите точки максимума и минимума, а также значения функции в этих точках.

5. Исследуйте характер выпуклости (найдите интервалы выпуклости и точки перегиба).

6. На основании результатов проведённого исследования постройте график функции. При этом, если возможно, найдите точки его пересечения с осями координат.

Отметим, что учёт свойств симметрии графика относительно осей или начала координат, а также периодичности функции (если таковые имеются) может существенно облегчить процесс исследования.

Пример 5.12. Исследовать функцию и построить её график.

1. Область определения ,  единственная точка разрыва (второго рода): при .

2. Асимптоты:

а) вертикальная  ось ;

б) правая наклонная:

; , – правая наклонная асимптота.

в) Вычисления при показывают, что также и левая наклонная асимптота.

3. Интервалы возрастания и убывания. . возрастает на и на ; убывает на .

4. Экстремумы. - точка минимума, .

5. Выпуклость. , , выпуклость вниз на и на .

6. Точки пересечения с осями координат: , следовательно

 абсцисса точки пересечения с осью .

Г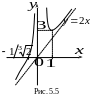 рафик функции имеет вид