5.2. Экстремумы функций. Наибольшее и наименьшее значения функции на отрезке.
Определение.
Функция
имеет в точке
максимум (минимум), если существует
такая окрестность точки
,
что для всякой точки
из этой окрестности, отличной от
,
справедливо неравенство
(соответственно
).
М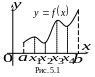
аксимум
или минимум
называется экстремумом функции
,
а точка
точкой экстремума
(максимума или минимума).
Замечание. Не следует путать максимум (минимум) функции с её наибольшим (наименьшим) значением, например, на отрезке .
Так, непрерывная
функция, изображенная на рис. 5.1, имеет
в точках
и
максимум, а в точках
и
минимум, причём
,
а своего наибольшего и наименьшего
значения данная функция достигает
вообще на границах отрезка
.
Определение.
Точка
,
в которой производная функции
равна нулю или терпит разрыв (при этом
не существует) называется критической
(или критической точкой первого рода).
Критическая точка
,
в которой
,
называется стационарной.
Теорема. (Необходимые условия существования экстремума).
Если функция
непрерывна на отрезке
и имеет в его внутренней точке
экстремум, то точка
является критической.
Обратное утверждение неверно.
Теорема.
(достаточные условия существования
экстремума, или его отсутствия). Если
существует окрестность
,
критической точки
,
в которой функция
непрерывна всюду, и дифференцируема
всюду, кроме, возможно , самой точки
,
причём
при
, (5.1)
при
,
то
точка максимума
(минимума). Если же
сохраняет знак во всей окрестности
,
кроме, возможно, точки
,
то в этой точке
не имеет экстремума.
Иногда бывает удобно воспользоваться другим достаточным условием существования (или отсутствия) экстремума.
Теорема. Если
и
, (5.2)
то точка максимума (минимума) функции .
Если же
,
,
,
то в точке
функция
не имеет экстремума.
П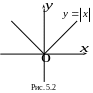
ример
5.3.
.
У этой непрерывной
функции одна критическая точка
,
в которой
не существует, причём
для
,
для
и, согласно условиям (5.1),
точка минимума
данной функции (рис.5.2).
Пример 5.4.
.
Функция дифференцируема всюду. Поскольку
,
то
единственная
критическая (стационарная) точка;
как справа, так и слева от точки
,
следовательно, в этой точки нет экстремума.
Пример 5.5.
.
Производная этой функции
не существует в точке
.
В этой же точке терпит разрыв второго
рода и сама функция (
при
),
т.е. условия её непрерывности в критической
точке не выполняются. Неправомерное
использование достаточного признака
экстремума (5.1):
при
и
при
привело бы к ошибочному выводу о том,
что
точка максимума
данной функции (см. её график в разделе
1.2)
Пример 5.6.
.
Функция непрерывна на
;
.
Критические точки
и
,
т.к.
,
а
не существует. Нетрудно убедиться, что,
согласно условиям (5.1),
точка максимума,
а
точка минимума
данной функции.
Отметим, что в стационарной точке исследование на экстремум можно провести и с помощью второй производной (условие(5.2)):
,
т.е.
и, следовательно
точка максимума.
Теорема.
Функция
,
непрерывная на отрезке
,
достигает своего наибольшего (наименьшего)
значения, либо в критических точках,
либо на концах отрезка
.