Лекция 1. Цель и задачи дисциплины

Имитационное моделирование – один из основных методов анализа и синтеза сложных систем, возникающих при изучении экономических или физических процессов и объектов на микро, макро и глобальном уровнях.

Целью преподавания дисциплины «Имитационное моделирование» яв­ляется усвоение студентами основных понятий и мето­дов имитационного моделирования, необходимых в профессиональной деятельности специалиста в области применения математических методов в экономике.

Введение

Имитационным моделированием называется воспроизведение поведения изучаемой системы на основе анализа ее структуры и наиболее существенных взаимосвязей элементов с целью получения информации о функциональных свойствах этого объекта.

Модель системы представляет изучаемый объект и выступает в роли относительно самостоятельной системы, позволяющей получить важнейшие сведения о самом объекте.

Компьютерное ИМ предполагает выполнение ряда последовательных действий.

1. Описание реальной системы с выделением структуры, динамического взаимодействия элементов, факторов неопределенности и состояний системы, в которых она может находиться.

2. Создание блоковой схемы объекта с указанием состояний его элементов и возможных переходов между ними.

3. Построение моделирующей программы на специальном языке ИМ или общем языке программирования.

4. Проигрывание различных возможных ситуаций на модели.

5. Верификация модели и программы на основе анализа полученных результатов и их сравнения с теорией процесса и (или) информацией о функционировании реального объекта.

ИМ следует рассматривать как статистический эксперимент, а его результаты представляют собой наблюдения. Любое утверждение относительно характеристик изучаемой системы является статистической гипотезой.

ИМ, по сравнению с обычными методами решения задач исследования операций является более гибким инструментом, особенно в части детализации поведения сложных систем.

Метод Монте-Карло (мк)

ИМ можно считать развитием метода МК, разработанного в 50-х годах прошлого века. Основная идея этого метода состоит в использовании выборок для получения оценок искомых характеристик изучаемых объектов. Задача, при этом, формулируется таким образом, чтобы алгоритм решения использовал случайные числа соответствующих законов распределения. Оказалось, что можно таким образом формализовать детерминированную задачу (вычисление определенных интегралов, например), чтобы решить ее с помощью выборок случайных чисел. Продемонстрируем это на примере. Пусть требуется найти площадь фигуры, ограниченной заданными линиями.

Пусть плоская фигура g составляет часть фигуры G. На фигуру G брошена случайная точка. Тогда вероятность попадания ее нa фигуру g равна отношению площади g к площади фигуры G : (геометрическая вероятность). Следовательно, если известна площадь , то . Используем этот подход для определения площадей фигур, заданных уравнениями границ.

Пример 1. Найти площадь фигуры, ограниченной линиями .

Построим указанные линии. Из Рис. 1 видно, что фигура, площадь которой необходимо найти полностью попадает в прямоугольник с основанием равным 6 и высотой 4 и площадью .

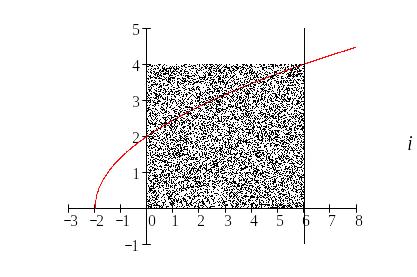
Рис. 1.

Формируем n случайных точек внутри этого прямоугольника.

. Здесь оператор дает случайное число, равномерно распределенное на интервале . Подсчитаем, какое число таких точек попадет на заданную фигуру при помощи программы

.

Вероятность попадания одной точки на фигуру g приближенно равна (и тем точнее, чем больше n) отношению числа точек попавших на фигуру к полному числу точек. и, тогда искомая площадь . С другой стороны, площадь фигуры равна определенному интегралу . Относительная погрешность метода МК 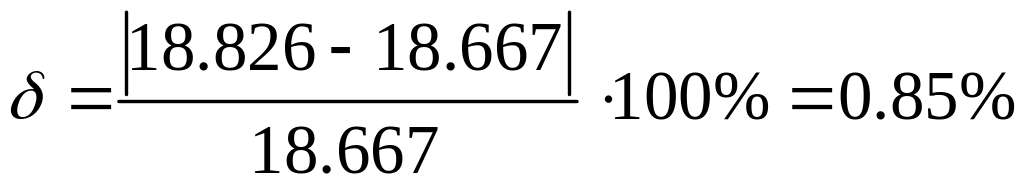. Повысить точность можно увеличением числа точек или (и) повторением расчета с последующим усреднением.

Пример 2. Найти площадь фигуры, ограниченной линиями . Найдем точки пересечения данных линий и построим график. Из чертежа видно, что фигура, площадь которой необходимо найти полностью попадает в прямоугольник с основанием равным 6 и высотой 4 и площадью .

Формируем n случайных точек внутри этого прямоугольника.

. Программа для подсчета, аналогична приведенной и нет необходимости ее приводить.

Вероятность попадания одной точки на фигуру g равна и тогда искомая площадь . Площадь фигуры равна определенному интегралу . Относительная погрешность метода МК в этом примере .

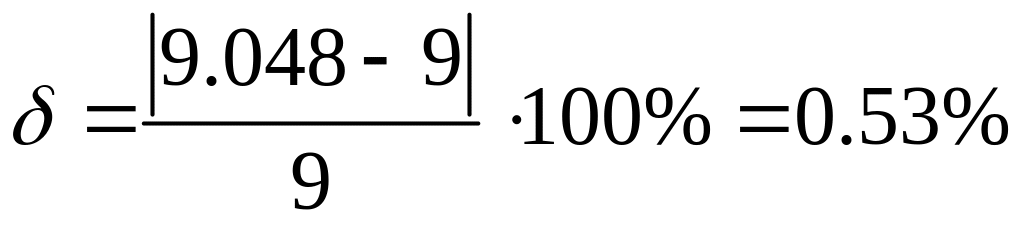Рассмотрим теперь Марковский случайный процесс, протекающий в системе.