Одноканальная смо с неограниченной очередью

Из СМО с ожиданием самой простой является одноканальная СМО с неограниченной очередью. Такие СМО часто встречаются в практике: врач, обслуживающий пациентов; телефон-автомат с одной будкой; ЭВМ, выполняющая заказы пользователей.

Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений. На эту СМО поступает поток заявок с интенсивностью ; поток обслуживания простейший и имеет интенсивность , .

Найти предельные вероятности состояний СМО, а также характеристики эффективности ее работы.

Запишем состояния СМО (состояния пронумерованы по числу заявок в системе):

канал свободен,

канал занят, очереди нет,

канал занят, одна заявка в очереди,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

канал занят; заявка в очереди,

и так далее.

Теоретически число состояний не ограничено (бесконечно). Граф состояний показан на рисунке 3

. . .

. . .

Рис. 3

Существуют ли в этом случае предельные вероятности состояний, ведь число состояний системы бесконечно?

Формула для определения имеет вид:

В скобке стоит сумма бесконечной геометрической прогрессии. Если знаменатель прогрессии , то сумму можно вычислить по формуле

Если , то ряд расходится, сумма растет неограниченно, СМО не может работать из-за неограниченно возрастающей очереди. Дальнейшие формулы справедливы только при .

Среднее число заявок в очереди одноканальной СМО и время ожидания обслуживания равно

.

Среднее число занятых каналов - Найдем среднее число заявок в системе:

,

и среднее время нахождения заявки в системе:

.

Пример. На железнодорожную сортировочную горку прибывают составы с интенсивностью состава в час.

Среднее время, в течение которого горка обрабатывает состав, равна 24 минутам. Составы, прибывшие в момент, когда горка занята, становятся в очередь и ожидают в парке прибытия, где имеются три запасных пути, на каждом из которых может ожидать один состав.

Состав, прибывший в момент, когда три запасных пути заняты, ставится на внешний путь. Станция платит штраф за пребывание состава на внешнем пути (а усл. ед. за 1 час). Вычислим вероятности состояний СМО для стационарного случая и коэффициенты эффективности работы горки. Вычислить штраф, который должна выплачивать станция за месяц из-за ожидания обслуживания на внешних путях.

Нас будут интересовать те состояния, при которых составы попадают на внешний путь:

один состав на горке, три в очереди на запасных путях станции, один на внешних путях,

один на горке, три на запасных путях, два на внешних путях и так далее.

Вычислим стационарные вероятности состояний СМО:

сост/час; час.; сост./час.

Теперь найдем вероятность того, что прибывающий состав попадает на внешний путь

Таким образом, в 41% случаев состав попадает на внешний путь.

Вычислим коэффициенты эффективности работы горки.

Среднее число составов, ожидающих в очереди (как в парке, так и вне его) -

состава, часа.

Среднее число составов в парке расформирования -

состава, часа.

Таким образом, составу приходится более 1,5 часов стоять в очереди.

Вычислим среднее время ожидания на внешних путях. Составим закон распределения случайной величины ; - число составов, поставленных на внешних путях.

	0	1	2	3	4	....
						....

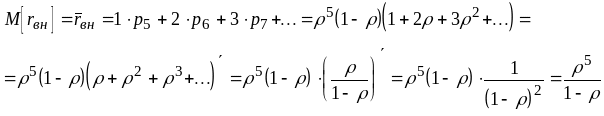В нашем примере:

Вычислим штраф за сутки:

Ш = 2 сост/час. · 24 час. · 0,41 · а = 19,66 а усл.ед.

Решим эту задачу имитационными методами. (Моделирующую программу можно найти в работе [3]).

Результаты для параметров эффективности

состава, часа.

Среднее число составов в парке расформирования -

состава, часа. Величина штрафа по результатам моделирования также близка к значению, полученному выше.

Все рассмотренные в этой лекции примеры показывают, как можно использовать ИМ для решения самых различных задач. Результаты показывают, что применение классических или моделирующих методов определяется лишь психологическими предпочтениями. Однако, существует большой класс задач прикладного характера, решение которых классическими методами затруднительно или вообще невозможно при современном состоянии развития методов прикладной математики. Рассмотрению таких задач и посвящена следующая лекция.