Марковская цепь с непрерывным временем

Имеется некоторая система с k состояниями. Переходы между состояниями происходят мгновенно в случайные моменты времени. Вероятности переходов из любого состояния Si в любое другое Sj являются функциями от времени pij(t). Если случайный процесс, протекающий в системе, обладает свойством отсутствия последействия, то говорят, что задана Марковская цепь с непрерывным временем [2]. 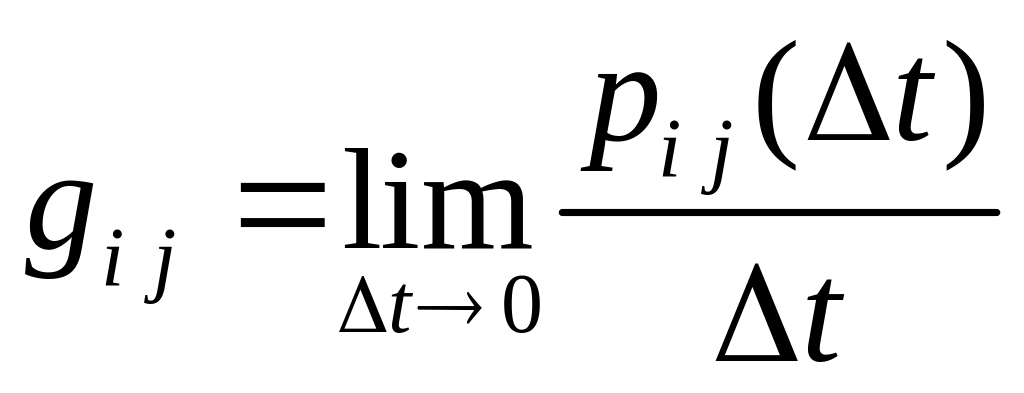Интенсивностью перехода из состояния Si в состояние Sj называется предел , где вероятность перехода на интервале времени .

Рассмотрим, для примера, Марковскую цепь с тремя состояниями. Пусть задана матрица интенсивностей переходов и начальное распределение вероятностей состояний

,

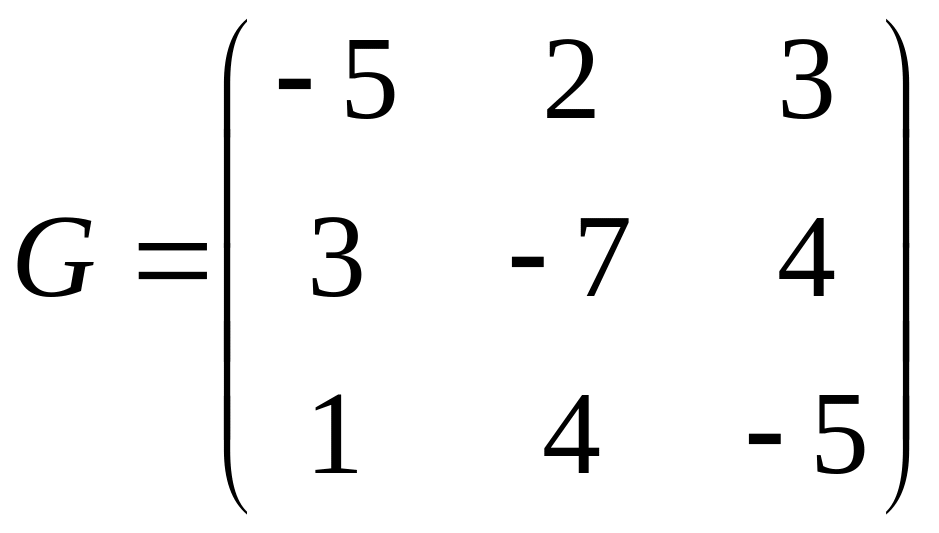Составим размеченный граф состояний этой Марковской цепи (Рис. 3). Очевидно, что данная цепь регулярна и имеет финальное распределение вероятностей состояний, совпадающее со стационарным распределением.

2. Найти стационарное распределение вероятностей состояний.

3. Выполнить моделирование системы и сравнить полученные результаты моделирования с результатами, полученными в пункте 2.

Решение.

1. Составим граф состояний.

2

S1

S2

3

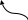
3 1 4 4

S3

Рис. 3.

По графу видно, что все состояния системы существенны и связаны между собой, поэтому цепь регулярна [2].

Запишем уравнения для вероятностей состояний.

Потоком вероятности из состояния в состояние называют произведение интенсивности этого перехода на вероятность состояния . Производная вероятности состояния будет равна сумме потоков «втекающих» в это состояние без потоков «вытекающих» из него. Тогда, например, для состояния можно записать по графу

или . Записывая по аналогии уравнения для других состояний, получим систему дифференциальных уравнений (Колмогорова).

.

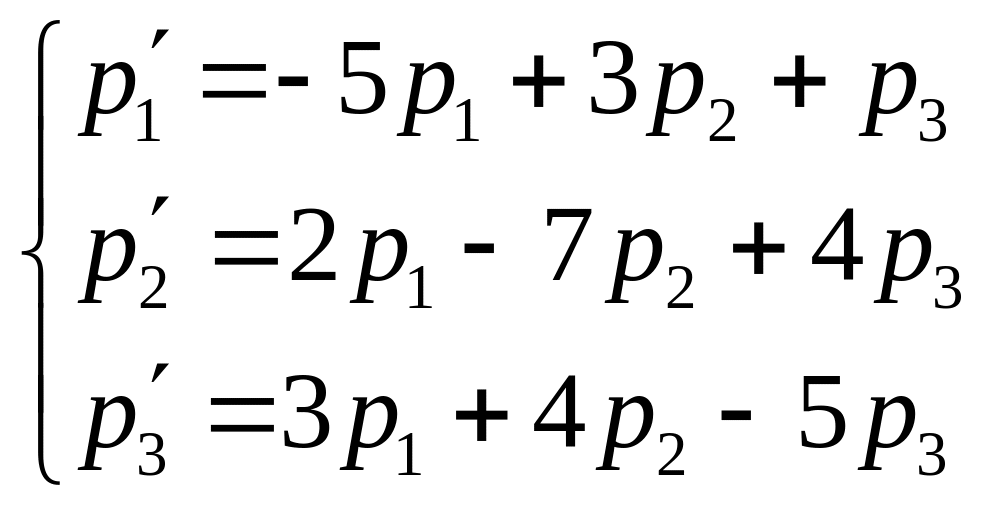При достижении стационарного состояния вероятности станут постоянными величинами и их производные будут равны нулю. Тогда из системы

совместно с очевидным условием ,

найдем стационарное распределение вероятностей состояний

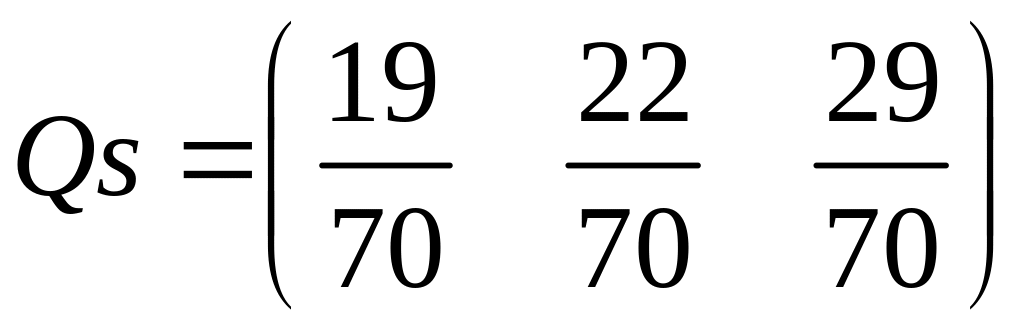
Моделирование процесса, протекающего в данной системе.

Введем переменный массив sj, элементы которого – суммарное время пребывания системы в данном состоянии j, время моделирования ; матрицу В – индикатор состояний (каждый столбец соответствует одному состоянию). Например, при выборе столбца 3 система находится в состоянии 2. Напомним, что в этом разделе элементы массивов нумеруются так 0,1,2,…

; .

Моделирующая программа.

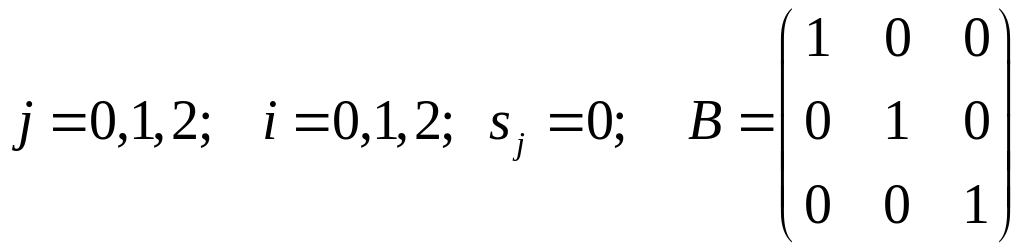Рассмотрим операторы программы по порядку. Задается начальное значение модельного времени t. Вводится матрица iw соответствующая начальному состоянию системы по индикатору состояний и строится цикл while до достижения времени моделирования tm. Определяется номер состояния k, в котором система находится в текущий момент времени. В цикле вычисляем все времена , через которые система может перейти в другое состояние. Находим минимальное из этих времен . Так как цепь Марковская, то она удовлетворяет условию отсутствия последействия, и случайные времена между переходами распределены по показательному закону. Они могут быть найдены с помощью оператора . Здесь 1 показывает, что вычисляется одно значение, а − интенсивность соответствующего перехода. Полученное время суммируется с временем, которое система провела в текущем состоянии s. Определяется номер ind состояния, в которое переходит система, и этот номер учитывается в индикаторе В. Отношения времени пребывания в каждом состоянии к полному времени моделирования, принимаются за оценки стационарных вероятностей состояний . Для рассмотренного примера и времени моделирования получим

.

Сравнивая результаты моделирования при различных прогонах с различными числами шагов и точные значения стационарных вероятностей состояний, делаем вывод о хорошей сходимости результатов.

Рассмотрим имитационную модель системы массового обслуживания.