
- •Конспект лекций по моделированию систем
- •§ 1. Основные понятия.
- •§ 2. Классификация моделей
- •§ 3. Этапы составления и исследования моделей.
- •§ 4. Имитационное моделирование.
- •§ 5.Элементы теории вероятности.
- •Способы вычисления вероятности
- •§ 6.Примеры основных случайных величин и их характеристик
- •§ 7.Построение датчика псевдослучайных чисел.
- •§ 7.1 Датчики для равномерного закона распределения
- •§ 7.2 Построение датчика псевдослучайных чисел для любого закона распределения
- •§ 7.3 Построение датчика по показательному закону распределения
- •§ 7.4 Построение датчика с помощью таблицы квантилей
- •§ 8. Потоки случайных событий. Пуассоновский поток.
- •§ 9.Связь потока Пуассона с показательным законом распределения
- •§ 10. Минимизация конечных автоматов.
- •§ 11. Моделирование работы конечного автомата
- •§12. Моделирование работы системы массового обслуживания
- •§ 13. Двумерные случайные величины и их законы распределения
- •§ 14.Понятие зависимых и независимых случайных величин
- •§15 Условное математическое ожидание линии регрессии.
- •§16 Числовые характеристики двумерных случайных величин Корреляционный момент
- •§17 Виды зависимости между случайными величинами.
- •§18 Нахождение на практике линейной регрессии.
§ 5.Элементы теории вероятности.
Основным понятием является понятие опыта.
Опыт – это эксперимент, который можно повторять неограниченное число раз при неизменных условиях.
Событие – это любой результат опыта или эксперимента
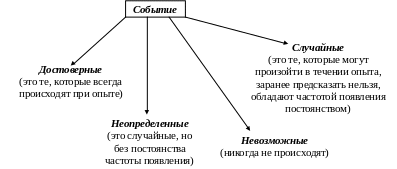
Вероятность – это некоторое число. Если А - случайное событие, то вероятность этого события находится в промежутке 0 ≤ P(А) ≤ 1, где 0 – это невозможное событие, 1 – достоверное событие. Чем ближе к единице, тем больше вероятность того, что событие достоверное.
Способы вычисления вероятности
Схема случаев.
Опыт сводится к схеме случаев, если обладает свойствами:
число элементарных исходов конечно;
элементарные исходы попарно несовместны;
все исходы равновозможные.
P(А)=m/n, где n – число элементарных исходов
m – число исходов благоприятного появления А
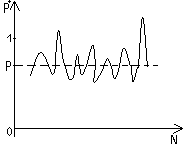
Статистическое определение вероятности.
Опыт: случайное событие А, N – число проведенных опытов, n – появлений событий А.
PN*( А) = n/m - частота появления события А.
![]()
З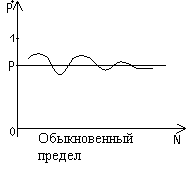
 амечание:
амечание:
Частота стремится в основном к вероятности.
Будут отклонения, но с ростом число таких
отклонений в процентном состоянии стремится к 0
Случайная величина – это любая числовая функция на множестве Ω, областью определения которой является множество Ω, а область значений множество действительных чисел.
Пространство элементарных исходов есть некоторое множество, в которое входят все элементарные исходы.
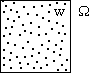 Ω={w}
Ω={w}
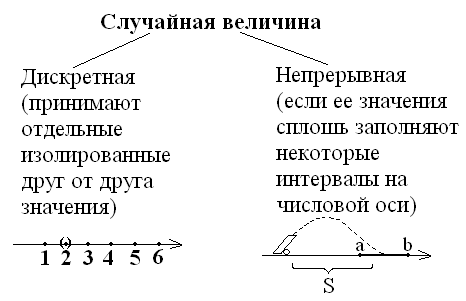
Для описания случайных величин используют законы распределения случайных величин.
Представление дискретной случайной величины:
X |
x1 |
x2 |
x3 |
… |
xn |
P |
p1 |
p2 |
p3 |
… |
pn |
Пример: для кубика выглядит так
X |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
P |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Представление непрерывной случайной величины:
Функция распределения
![]()
Механический смысл закона распределения для дискретной случайной величины:
![]() mi=1/6,
где i – это каждая точка.
mi=1/6,
где i – это каждая точка.
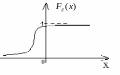
Для непрерывной случайной величины:
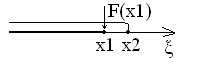
x1<x2, F(x1)≤ F(x2)
![]() ,
,
![]()
F(x) – монотонно возрастающая функция
![]()
![]()
Механическая аналогия – это плотность массы, с которой вероятность размазана по всей числовой оси
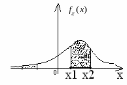
![]()
Числовые характеристики
X – случайная дискретная величина
-
X
x1
x2
x3
…
xn
P
p1
p2
p3
…
pr
Математическое ожидание – это средняя точка, около которой разбросаны значения вероятностей
![]()
Математическое ожидание характеризует центр рассеивания вокруг которого разбросаны случайные значения.
X – непрерывная случайная величина
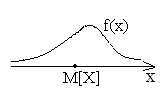
Здесь M[X] – центр тяжести системы материальных точек.
![]()
Дисперсия – характеризует величину разброса случайных значений вокруг математического ожидания.
![]()
![]()
![]() Механический смысл – координаты точки,
момент инерции.
Механический смысл – координаты точки,
момент инерции.
Среднеквадратическое отклонение от математического ожидания
![]()
