. Оптика

13. Хвильова оптика

Хвильова оптика вивчає хвильові властивості електромагнітного випромінювання та його взаємодію з речовиною у видимому інтервалі довжин хвиль

,

з частотами

,

тобто на таких частотах і довжинах хвиль, які викликають зорове відчуття образів людським оком. Таке випромінювання ще називають світлом.

Властивості світла проявляються у таких явищах як інтерференція, дифракція та дисперсія, поляризація, відбивання, поглинання та розсіювання, теплового випромінювання речовиною. Вирішення проблеми квантування світла та його корпускулярно-хвильової природи стало першим кроком у становленні квантової механіки. Саме це коло питань буде предметом розгляду нижче.

Надалі ми будемо розглядати плоскі хвилі, що розповсюджуються в напрямкові осі ОХ і описуються рівняннями

,

де – амплітуди електричної та магнітної складових (плоскі хвилі мають хвильовий фронт у вигляді безконечної площини). Речовина, в якій розповсюджуються хвилі, характеризується діелектричною  та магнітною  проникливостями, фазовою груповою швидкістю . Інтенсивність електромагнітної хвилі можна записати через електричну складову

, (1)

або магнітну складову

. (2)

Якщо врахувати, що показник заломлення світла у речовині , то вирази для інтенсивності можна записати у вигляді

. (3)

13.1. Інтерференція світлових хвиль

13.1.1.Додавання когерентних хвиль

Дві хвилі

, (1)

де

(2)

називаються когерентними, якщо , а різниця фаз

(3)

не залежить від часу. В результаті додавання хвиль (1) за допомогою метода фазових діаграм (див.п. 4.8) одержимо

, (4)

де

, (5)

. (6)

Фазова діаграма представлена на Мал. (див. Мал.140). Вираз (5) можна записати через інтенсивність

(7)

В (7) доданок

(8)

називається інтерференційним членом. В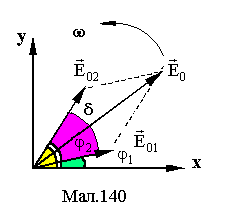 ираз

є середнім значенням cos за період.

Різниця фаз може залежати від часу, але коли за період вона змінюється менше ніж на , то середнє значення за період буде відмінне від нуля. Такі хвилі називаються частково когерентними. У противному

_. (9)

Таким чином у випадках повної чи часткової когерентності інтерференційний член (8) буде відмінним від 0.

Розпишемо різницю фаз (3) у явному виді

і представимо її так

(10)

У (10) у середовищі з показником заломлення світла n

 довжина хвилі у вакуумі,

 довжина хвилі у середовищі,

 хвильове число,

 величина оптичного ходу хвилі,

 оптична різниця ходу світла.

Якщо дві когерентні хвилі розповсюджуються у одному середовищі, то і називається різницею ходу світла.

13.1.2. Розподіл результуючої амплітуди в умовах інтерференції

Під інтерференцією світла розуміють перерозподіл енергії двох або більше взаємодіючих когерентних електромагнітних хвиль, що проявляється в підсиленні та ослабленні інтенсивності випромінювання в певних областях простору. Явище інтерференції лежить в основі процесу поширення хвиль у речовині та створенні образів в оптичних системах.

При додаванні двох когерентних або частково когерентних хвиль одного напрямку при певних умовах може бути відмінним від нуля інтерференційний член . Розглянемо взаємодію двох когерентних хвиль, коли різниця фаз є сталою, тобто і вони розповсюджуються у одному середовищі з показником заломлення n. Максимум інтерференції буде спостерігатися при умові , тобто

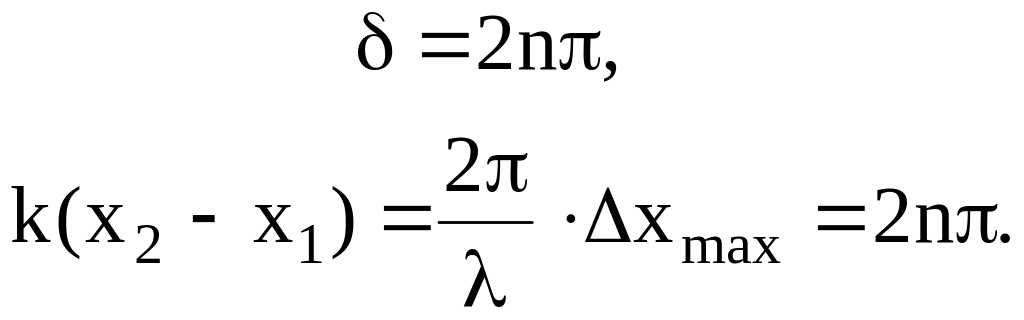
При цьому різниця ходу променів становить ціле число довжин хвиль

. (1)

Амплітуда результуючого коливання при цьому буде максимальною

(2)

Мінімум інтерференції буде спостерігатися при умові , тобто

.

При цьому різниця ходу променів становить напівціле число довжин хвиль

. (3)

Амплітуда результуючого коливання при цьому буде мінімальною

(4)