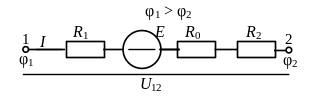- •120302 – Земельный кадастр
- •Оглавление
- •1 Указания к выполнению Домашнего Задания
- •2 Расчет электрической цепи постояного тока
- •2.1 Краткие теоретические сведения
- •2.2 Задание 1
- •2.2 Задание 2
- •3 Расчет электрической цепи однофазного синусоидального тока
- •3.1 Краткие теоретические сведения
- •3.2 Задание 3
- •Библиографический список
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИИСКОЙ ФЕДЕРАЦИЙ
|
||
|
Кафедра автоматики и
электротехники
ОПД.Ф.04 ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Методические указания
к выполнению домашнего задания по дисциплине
Специальность
120302 – Земельный кадастр
Уфа 2011
УДК 621.3.024/025:378.147
ББК 22.33:78.58
Рекомендовано к изданию методической комиссией факультета З и ЛХ (протокол № _9_ от _27 июня_2011 г.)
Составитель: ст.преподаватель кафедры автоматики и электротехники
Толмачева Л.Р.
Рецензент: д.т.н., профессор кафедры электрических машин и электрооборудования Аипов Р.С.
Ответственный за выпуск: заведующий кафедрой автоматики и электротехники
доцент Галимарданов И.И.
Оглавление
1. Указания к выполнению домашнего задания |
4 |
2. Расчет электрической цепи постоянного тока |
5 |
3. Расчет электрической цепи однофазного синусоидального тока |
9 |
Библиографический список |
20 |
1 Указания к выполнению Домашнего Задания
В процессе выполнения домашнего задания студенты должны приобрести навыки расчета линейных электрических цепей. Расчет линейных цепей постоянного тока ведется методом преобразований, методом применения законов Кирхгофа. Исходные параметры цепи, ее электрическая схема задаются в индивидуальных заданиях.
При выполнении домашнего задания следует пользоваться общепринятыми обозначениями, расшифровывая их при первом применении. Решение должно сопровождаться краткими, но четкими пояснениями. Текст, формулы и числовые выкладки должны быть написаны четко и аккуратно. Все единицы измерения должны соответствовать Международной системе единиц СИ. Схемы должны вычерчиваться с соблюдением масштаба и ГОСТов.
При решении задачи не следует изменять однажды принятые направления токов, напряжений, нумерацию узлов и т.д.
Домашнее задание должно состоять из пояснительной записки, которая выполнена на листах формата А4 (297210) мм. Рекомендуемый объем пояснительной записки составляет:
- при выполнении рукописным способом – 10 с.;
- при использовании средств оргтехники – 8 с.
Пояснительная записка оформляется согласно требованиям СТП БГАУ 2009 и должна включать:
- титульный лист;
- задание на работу с указанием типовых схем и исходных данных для ее расчета;
- оглавление;
- расчет электрической цепи с применением программных продуктов (Math Cad);
- проверку правильности решения;
- библиографический список.
2 Расчет электрической цепи постояного тока
2.1 Краткие теоретические сведения
При расчетах неразветвленных и разветвленных линейных электрических цепей постоянного тока могут быть использованы различные методы, выбор которых зависит от вида электрической цепи.
При расчетах сложных электрических цепей во многих случаях целесообразно производить их упрощение путем свертывания, заменяя отдельные участки цепи с последовательным, параллельным и смешанным соединениями сопротивлений одним эквивалентным сопротивлением с помощью метода эквивалентных преобразований (метода трансфигураций) электрических цепей.
Электрическая цепь с последовательным соединением сопротивлений (рисунок 1, а) заменяется при этом цепью с одним эквивалентным сопротивлением Rэк (рисунок 1, б), равным сумме всех сопротивлений цепи:
Rэк
= R1
+ R2
+…+ Rn
=
![]() ,
,
где R1, R2 … Rn – сопротивления отдельных участков цепи.
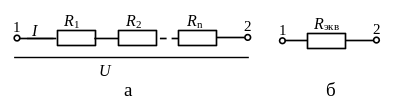
Рисунок 1 Электрическая цепь с последовательным соединением сопротивлений
При параллельном соединении сопротивлений все сопротивления находятся под одним и тем же напряжением U (рисунок 2). Электрическую цепь, состоящую из параллельно соединенных сопротивлений, целесообразно заменить цепью с эквивалентным сопротивлением Rэк, которое определяется из выражения
![]() ,
,
где
![]() - сумма величин, обратных сопротивлениям
участков параллельных ветвей
электрической цепи;
- сумма величин, обратных сопротивлениям
участков параллельных ветвей
электрической цепи;
Rj – сопротивление параллельного участка цепи;
n – число параллельных ветвей цепи.
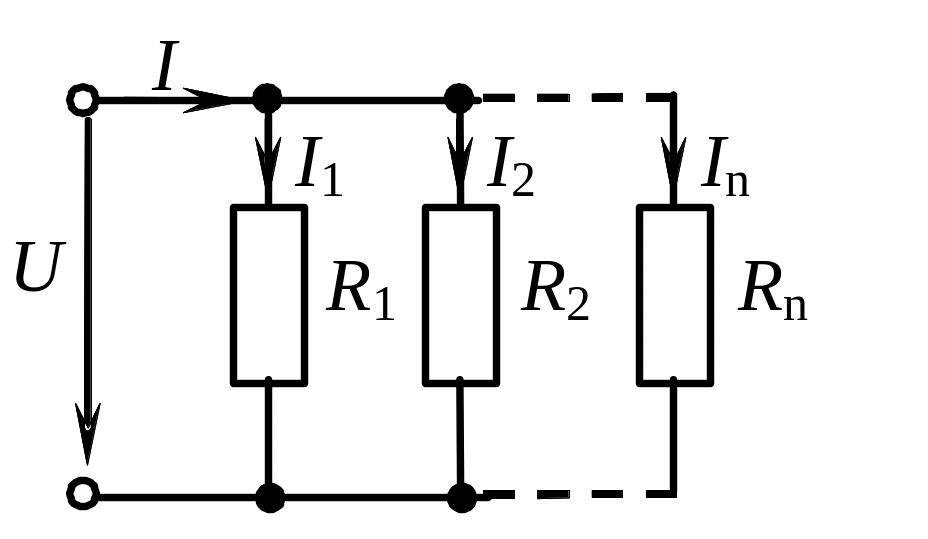
Рисунок 2 Электрическая цепь с параллельным соединением сопротивлений
При смешанном соединении сопротивлений, т.е. при наличии участков электрической цепи с последовательным и параллельным соединением сопротивлений, эквивалентное сопротивление цепи определяется в соответствии с выражением
Rэк
=
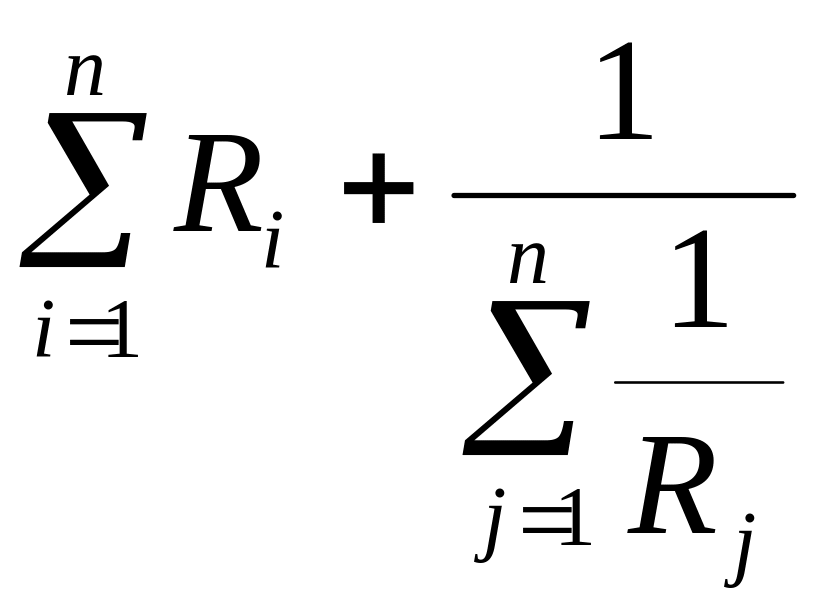 .
.
Во многих случаях оказывается целесообразным также преобразование сопротивлений, соединенных треугольником, эквивалентной звездой (рисунок 3).

Рисунок 3 Электрическая цепь с соединением сопротивлений треугольником и звездой
При этом сопротивления лучей эквивалентной звезды определяют по формулам:
R1
=
![]() ;
R2
=
;
R2
=
![]() ;
R3
=
;
R3
=
![]() ,
,
где R1, R2, R3 – сопротивления лучей эквивалентной звезды сопротивлений;
R12, R23, R31 – сопротивления сторон эквивалентного треугольника сопротивлений. При замене звезды сопротивлений эквивалентным треугольником сопротивлений, сопротивления его рассчитывают по формулам:
R31 = R3 + R1 + R3R1/R2; R12 = R1 + R2 + R1R2/R3; R23 = R2 + R3 + R2R3/R1.
Законы цепей постоянного тока.
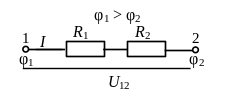
Для участка цепи, не содержащего источник энергии (например, для схемы рисунок 4, а), связь между током I и напряжением U12 определяется законом Ома для участка цепи:
I
=
![]() ,
,
где φ1 и φ2 – потенциалы точек 1 и 2 цепи;
U12 = φ1 – φ2 – напряжение (разность потенциалов) между точками 1 и 2 цепи;
Σ R – сумма сопротивлений на участке цепи;
R1 и R2 – сопротивления участков цепи.
а |
б |
Рисунок 4 Электрическая схема участка цепи: а – не содержащая источник энергии; б – содержащая источник энергии
Для участка цепи, содержащей источник энергии (рисунок 4, б), закон Ома записывают в виде выражения
I
=
![]() ,
,
где Е – ЭДС источника энергии;
Σ R = R1 + R2 – арифметическая сумма сопротивлений участков цепи;
R0 – внутреннее сопротивление источника энергии.
Законы Кирхгофа устанавливают соотношения для токов и напряжений в разветвленных электрических цепях различной конфигурации.
Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю
![]() ,
,
где Ik – ток в k-й ветви.
Второй закон
Кирхгофа:
алгебраическая
сумма напряжений вдоль замкнутого
контура равна нулю или алгебраическая
сумма падений напряжений на сопротивлениях
контура
![]() равна алгебраической сумме э.д.с.
источников
равна алгебраической сумме э.д.с.
источников
![]() ,
действующих
в этом контуре:
,
действующих
в этом контуре:
![]() =
.
=
.
При расчете электрических цепей методом применения законов Кирхгофа выбирают условные положительные направления токов в ветвях, затем выбирают замкнутые контуры и задаются положительным направлением обхода контуров. При этом для удобства расчетов направление обхода для всех контуров рекомендуется выбирать одинаковым (например, по часовой стрелке).
Число уравнений, составленных по первому закону Кирхгофа, берется на единицу меньше числа узлов Nу в цепи: NI = Ny – 1. При этом токи, направленные к узлу, условно принимаются положительными, а направленные от узла – отрицательными.
Остальное число уравнений NII = NВ – Nу + 1 составляется по второму закону Кирхгофа, где NВ – число ветвей.
При составлении уравнений по второму закону Кирхгофа ЭДС источников принимаются положительными, если направления их совпадают с выбранным направлением обхода контура, независимо от направления тока в них. При несовпадении их записывают со знаком «–». Падения напряжений в ветвях, в которых положительное направление тока совпадает с направлением обхода, независимо от направления ЭДС в этих ветвях – со знаком «+». При несовпадении с направлением обхода падения напряжений записываются со знаком «–».
В результате решения полученной системы из N уравнений находят действительные значения определяемых величин с учетом их знака. При этом величины, имеющие отрицательный знак, в действительности имеют направление, противоположное условно принятому. Направления величин, имеющих положительный знак, совпадают с условно принятым направлением.
Взаимосвязь между всеми видами мощностей в электрической цепи (баланс мощностей) определяется из уравнения:
ΣР1 = ΣР2 + ΣРп,
где ΣР1 = ΣЕI – алгебраическая сумма мощностей источников энергии;
ΣР2 – алгебраическая сумма мощностей потребителей (полезная мощность) (Р2 = UI);
ΣРп = ΣI2R0 – суммарная мощность, обусловленная потерями в сопротивлениях источника.