§11. Варіаційні задачі з рухомими межами.

Введемо на множині G = {у(х)| у С⁽¹⁾(а,b)} функціонал

J[y(x)]= F(x,y,y')dx , a≤ x₀ < x₁ ≤b.

Задача знаходження екстремуму цього функціонала при умовах

(*) y(х_о) = φ_о(х_о), у(х₁) = φ₁(х₁) є варіаційною задачею з рухомими кінцями.

Якщо функція у G реалізує екстремум функціоналу при умовах (*), то

виконуються: а) рівняння Ейлера = 0;

b) умови трансверсальності

Якщо один з кінців закріплений, то виконується тільки одна з умов трансверсальності. Якщо гранична точка (х_1, у(x₁)) переміщується лише по вертикальній прямій, то умова трансверсальності перетворюється в = 0.

Отже, для розв'язання найпростішої задачі J[y(x)]= F(x,y,y')dx з

рухомими межами, треба:

1.Написати і розв'язати рівняння Ейлера. Одержимо сім'ю

екстремалей у = f(х,с_1;с₂).

2 . З умов трансверсальності і з рівнянь

визначити сталі с₁ , с₂, х₀, х₁.

3 . Визначити потрібну екстремаль.

Приклад. Знайти допустиму екстремаль функціонала

J[y(x)]= (у' - y² ) dx при умові, що кінці належать лініям у = - х + 1, у =2х.

Розв'язання. Складемо рівняння Ейлера: у" + у = 0. Його розв'язок

у(х) = c₁ sinх + с₂ соsх ;

у'(х) = c₁ соsх - с₂ sinх.

Запишемо умови трансверсальності

с₂ = -0,8; c ₁= - 1,6.

Відповідь. Рівняння екстремалі: у(х) = - 1,6 sin х - 0,8 соsх.

Задачі. Знайти допустимі екстремалі функціоналів.

1. J[у(х)]= при умовах у = х²; у = х-5. В. у = - х +

2. J[у(х)]= (х²у' ² –ух)dх при умовах у = 2х - 1; у = х².

В. у =

3. J[у(х)]= (у + 2ху' +у'²)dх при умовах у = 2х+1; у = -х + 2.

В.у= + 2,24.

4. Знайти найкоротшу відстань від точки А(1;0) до еліпса 4х² + 9у² = 36.

B.d=

5. Знайти найкоротшу відстань від точки А(-1;5) до параболи у² = х.

В. d=

Вказівка до задач 4 і 5. Задачі зводяться до знаходження екстремуму (мінімуму)

інтеграла J[у(х)]= при умові, що лівий кінець задовольняє умові у(х₀) = у_о, а правий у = f(х).

Приклад. Знайти умову трансверсальності для функціонала

J[у(х)]= f(х,у)е^arctgy' , f (x,y)≠0

Розв 'язання. Нехай лівий кінець екстремалі закріплений в точці А(х_о,y_о), а правий - В(х_1, у₁) може переміщуватись по кривій у = ψ(х). Тоді

Умова трансверсальності має вигляд, бо f (х ,у) ≠ 0

Геометрично ця умова означає, що екстремалі у = у(х) повинні перетинати криву у = ψ(х), по якій ковзає гранична точка В(х₁,у₁), під кутом π/4.

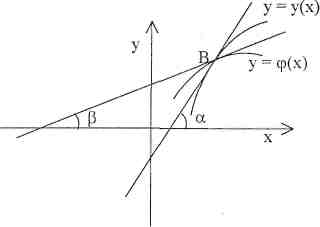
Дійсно, тут tgα = у', tgβ = ψ ' , ,то згідно (*)

tg(β-α) = -1 = tg ( , що і треба було

довести.

Приклад 3. Знайти відстань між параболою у = х² і прямою х - у = 5.

Розв 'язання. Задача зводиться до знаходження екстремального значення

функціонала J[у(х)] = при умові, що лівий кінець екстремалі

переміщується по кривій у = х², а правий - по прямій у = х - 5. Тут φ(х) = х²,

ψ(х) = х -5. Загальний розв'язок рівняння Ейлера: у = c₁ x + с₂, де c₁ і с₂ — довільні сталі, які треба визначити.

Умови трансверсальності мають вигляд:

, де у' = с₁. Для визначення с₁ і с₂, x₁ , x_о маємо ще рівняння

Ми одержали систему чотирьох рівнянь відносно невідомих с₁, с₂, х_1, х₀:

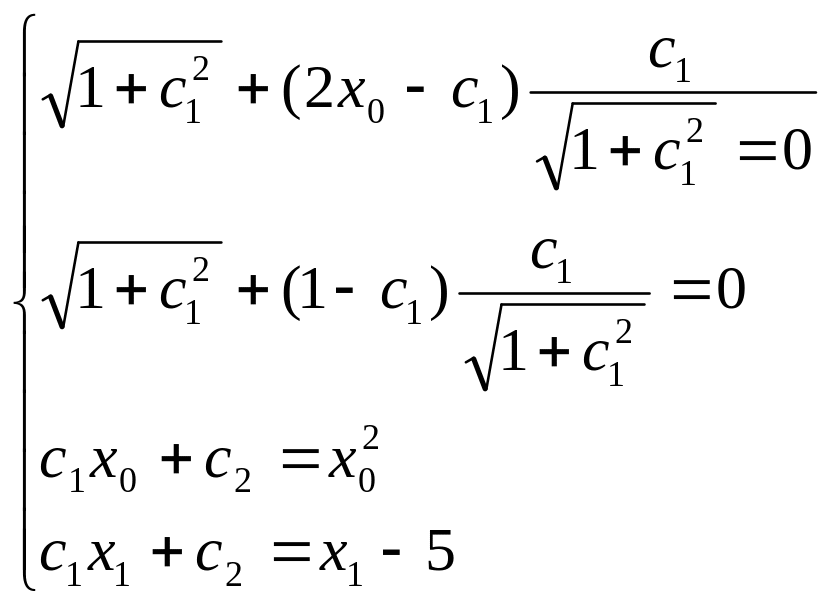
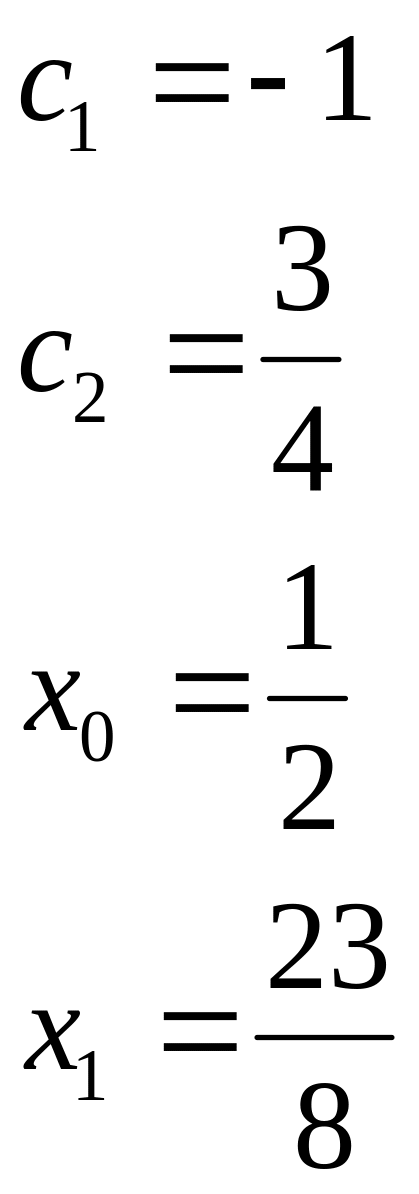
Отже рівняння екстремалі має вигляд: у = - х + і відстань між заданими

параболою і прямою дорівнює

Задачі.

6. Знайти відстань від точки А(1;0) до еліпса 4х² + 9у² = 36.

4 В.

7. Знайти відстань від точки А(-1;5) до параболи у² = х.

В.

8. Знайти відстань між колом х² + у² = 1 і прямою х + у = 4.

В.

9. Знайти відстань від точки А(-1;3) до прямої у = 1 -3 х .

В.

10. Знайти функцію, на якій може досягатись екстремум функціонала

J[y(x)] = (y'² -y'²)dx , у(0) = 0, якщо другий кінець ковзає по прямій х = π/4.

В. у ≡ 0

Приклад 4 . Знайти допустиму екстремаль функціоналу

J[у(х)] = при умові , що кінці належать лініям y=-x+1, y=2x .

Розв’язання . Складемо рівняння Ейлера :

Pозв’язок його має вигляд

Умови трансверсальності дають:

c₂ =-0,8 ; c₁=-1,6.

В. рівняння екстремалі c₂ =-0,8 ; c₁=-1,6.

Y(x)=-1,6 sinx – 0,8cosx

Приклад 5.

Знайти найменшу відстань між прямою у=-х і гіперболою .

Розв’язання . Нехай (a₁ , - a )- точка прямої , а (b , ) - точка гіперболи . Тоді подвоєний квадрат відстані між цими точками 2(a-b)²+2(a+ )²=

= 4a²-4a(b- )+2(b²+ ) =(2a-b+ )²-(b- )²+2 (b²+ ) ≥ b²+ +2 ≥4.

Знак рівності має місце , якщо одночасно виконуються рівності b²=1,

2a-b+ =0, тобто b= 1 i a=0 . Отже , шукана відстань .

Задача. Розв’язати задачу методами варіаційного числення.