§9. Умовний екстремум функціонала.

Задачі визначення екстремуму функціоналу, в яких на допустимі криві накладаються додаткові обмеження - умови зв'язку, називаються задачами на умовний екстремум.

Нехай на множині G= {у(х)| у = (у₁ ,y₂..., у_n), у_i (х) С⁽¹⁾(а,b), і = ,

у(а) = (у₁⁽⁰⁾, ..., у_n⁽⁰⁾), у(b) = (у₁⁽¹⁾, ..., у_n⁽¹⁾)}, визначено функціонал.

J[y(x)]= F(х,у₁,...,у_n,,у'_n,,…,у'_n,)dx , де функція F диференційовна по

кожній змінній потрібну кількість раз. Екстремум всього функціонала шукається при додаткових рівняннях зв'язку.

m<n.

Якщо у(х) G задовольняє рівняння зв'язку і реалізує екстремум

функціоналу, то існують такі функції (х), j = , такі, що вектор-функція

у(х) є екстремаллю функціонала

J[y(x)]= (F +

Ф(х,y,у') = F(х, у, у') + - функція Лагранжа.

Екстремум функціоналу при рівняннях зв'язку знаходяться з системи

(*) , яка доповнюється рівняннями зв'язку. З

системи знаходяться i

Приклад 1. На множині G = {(у_1, у₂)| y_i С⁽¹⁾ (0, /2), і=1,2, у(0)=(1,-1), у(π/2)=(1,1)} знайти екстремум функціоналу

J[y(x)]= (y ₁^{2 +} y²₂ - y '₁² - y '₂² )dx при умові у₁ -у₂ - 2соsх = 0. о

Розв 'язання. Складемо функцію Лагранжа

Ф = y ₁^{2 +} y²₂ - y '₁² - y '₂² +λ(x)(y₁ –y₂ -2 соs х).

Система (*) має вигляд

Додаємо їх: 2(у₁" + у₂") + 2(у_] + у₂) = 0 у₁ + у₂ = с₁ соsх + с₂ sinх. З граничних умов маємо c₁ = 0, с₂ = 2. Значить, у₁ + у₂ = 2sinх. Крім того, маємо рівняння зв'язку у₁ - у₂ = 2соsх. Тому у₁ = соsх + sinх, у₂ = sin х – соs х. Таким чином,

y ₁^{2 +} y²₂ - y '₁² - y '₂² = (соsх + sinх)² + (sinх-соsх)² -(-sinх + соsх)² - (соs х + sinх)² =

=0

Приклад 2. Знайти екстремалі і екстремум функціоналу

J[y(x)]= (y ₁² +2 y '₁² + y '₂² )dx , y(0)= (1,0); y (1)= (e + ; )при умові

y'₁-у₂=0.

Розв'язання.

Складемо функцію Лагранжа

Ф= y ₁² +2 y '₁² + y '₂² + λ(y'₁ - у₂). Тому екстремаль у(х) = (у₁(х), у₂(х)) задовольняє системі рівнянь

Виключаючи λ(х), маємо у₁ - 2у₁" + у₂"' = 0, що з врахуванням рівняння

зв'язку має вигляд у₁ ^IV - 2у₁ " + у₁ = 0. Значить, у₁ = (c₁ x + с₂)е^х + (с₃х + с₄)е ^-х,

у₂ = (c₁ x + c₁ + с₂)е^х - (с₃х + с₄ - с₃)e ^-х. Використовуючи граничні умови,

одержуємо у₁ = хе^х + е ^-х, у₂ = (х + 1)е^х – е ^-х, J _ехstr =

Задачі. Знайти екстремалі функціоналу:

1. J[y(x)]= , у(0) = (1,2); у(1) = (2,1) при умові

2у₁ - у₂ - 3х = 0.

В. у₁ = х + 16 у₂ = -х +2; 1_ехtr = .

2. J[y(x)]= (y'²₁+ y'₂²)dх, у(0) = (-1,0);y(1) = (-1,1) при умові

у₁ + у₂ =2х² + х+1

В. у₁ =х²-х-1,у₂ = х³; J_ехtr = 5/3.

3. J[y(x)]= (y'²₁+ y'₂²)dх ,у(0) = (1,0) ;,у(π/2) = ( ), при умовi

y₁'=у₂+sinх.

В. у₁ = sinх , у₂ = соsх- sinх; J_extr =

4. J[y(x)]= ( 2у₁ у₂+у' ₁²+у' ₂²)dх, у(0) = (-1,1); у( ) = ( + 1)

при умові у'₁ + у₂' = 4х.

В. у₁ = х² - соsх - sinх, у₂ = х² + соsх + sinх; J_ехtr =

§10. Ізопериметричні задачі.

Задача визначення екстремуму функціонала

J[y(x)]= F(х,у₁,у₂,...,у_n ,у'₁,у'₂,...,у'_п)dх при умовах

F_j (х,у₁,у₂,...,у_n ,у'₁,у'₂,...,у'_п)dх = c_j , j = називається

ізопeриметричною задачею. Якщо у = (у₁(х),у₂(х),...,у_n(х)) G задовольнять умовам зв'язку і дають екстремум функціоналу, то існують сталі λ₁ , λ ₂, ..., λ _т, що вектор-функція у(х) є екстремаллю функціоналу

J * [у] =, 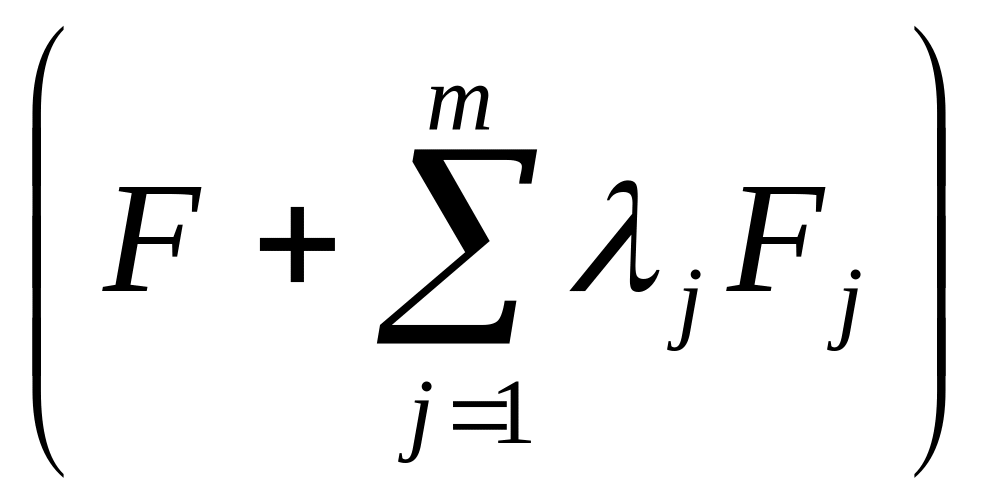d х = )Ф(х, у, у')dх.

Ф = - функція Лагранжа.

Приклад 1. Знайти екстремалі в ізопериметричній задачі.

J[y(x)]= у' ²dх, у(0) = 1, у(1) = 6 при умові у(х)dх = 3.

Розв'язання. Складемо допоміжну функцію Лагранжа: F = у'² + λу і запишемо рівняння Ейлера:

(2у') = 0; у" = ; у' = х + с₁; у(х) = х² +с₁ х + с₂.

З граничних умов визначаємо с₂ = 1; + с₁ = 5; з умови

( х² + с₁ х + 1)dx = 3 знаходимо + = 2 с₂ = 1; c₁ = 2; λ= 12.

Рівняння екстремалі: у(х) = 3х² + 2х + 1.

Задачі. Знайти екстремалі в ізопериметричних задачах:

1.J[y(x)]= (x + y'² )dx ; y(0) = 0; у(1) = 0 при умові у(х)dх = 2.

В. у = -12(х²-1)-min;

2.J[y(x)]= (х² + у'²)dх; у(0) = 1; у(1) = 0 при умові у{х)сdх = 3.

В.у = -15х²+ 14х+1 -min;

3. J[y(x)]= у'²dх; у(0) = у(π) = 0 при умові у²(х)dx = 1 вважати (λ < 0).

2 . В. у = ± sinх -min;

4.Знайти екстремалі ізопериметричної задачі J[y(x)]= = (у'² + х²)dх при

умові y ² (х)dx = 2; у(0) = 0; у(1) = 0. В. у = ± 2 sinх ( ), n Z.

5. Знайти екстремалі ізопериметричної задачі J[y(x)]= у'²dх при умові

уdх = а; де а - стала.

В. у = λх² + c₁ x + с₂, де λ, с_1, с₂ визначаються з граничних умов і із ізопериметричної умови.

6. Написати диференціальне рівняння екстремалей ізопериметричної задачі про

екстремум функціоналу J[y(x)]= (р(х)у'² + q(х)у² )dх при умові

r(х)y ²dx = 1;у (0) = 0;у(х₁) = 0.

В. (р(х)у' + (λr(х)-q(х))у = 0; у(0) = 0; у(х₁) = 0. Тривіальний

розв'язок у ≡ 0 не задовольняє ізопериметричну умову.

7. Знайти екстремаль в ізопериметричній задачі про екстремум функціоналу.

J[у(х),z(х)]= ( у'² + z'² - 4хz'- 4z)dх при умові (у'² -ху'-z '²)dх = 2;

у(0) = 0,z(0) = 0,у(1)=1,z(1)=1.В.у=- х²+ х; z= х.

Приклад 2. Знайти допустимі екстремалі функціоналу у'²dх, у(0) = 0,

у(1)= 5 при умові хуdх = 1.

Розв'язання. Складемо функцію Лагранжа Ф = у'² + λху і запишемо

рівняння Ейлера для функціонала (F + )dх і λх - 2у" = 0. Звідси

знаходимо: у = х³ + с₁ х + с₂. З граничних умов маємо у(0) = с₂ = 0,

у(1) = 5, а з обмеження знаходимо хуdх =

1.0тже ми одержали систему рівнянь = 5, 1, з якої слідує,

що с₁ = 0, λ=60. Отже, допустимою екстремаллю є крива у = 5х³ .

Задачі. Знайти допустимі екстремалі в ізопериметричних задачах:

8. y'²dх,у(0) = 0, у(1)= 1, уdх = 0, хуdх = 0. В. у = 3х- 12х² + 10х³.

9. ysinхdх, у(0) = 0, у(π) = 0, у'²dх = , В. у = ± sinх.

10. ydх, у(-1) = 0,у(1) = 0, . В. у = ±

Приклад 3. Знайти екстремаль в ізопериметричній задачі про екстремум

функціоналу J[у(х),z(х)]= ( у'² + z'² - 4хz'- 4z)dх при умові

('у - ху' -z'² )dх = 2.

Розв'язання. Складаємо допоміжний функціонал

Ф = J[у(х),z(х)]= ( у'² + z'² - 4хz'- 4z)dх , у(0) = 0,z(0) = 0,у(1)=1,z(1)=1 при умові (у'² +z'² -4хz'-4z + λ(у'² - ху' - z'²))dх і виписуємо для нього систему рівнянь Ейлера :

розв'язуючи яку, одержимо у(х) = ;

Граничні умови дають с₁ = ; с₂ = 0; с₃ = 2(1 -λ); с₄ = 0, то у(х)=

Для знаходження λ скористаємося ізопериметричною умовою. Оскільки то

, звідки будемо мати рівняння для визначення λ:

Підстановкою з умови-зв'язку маємо, що λ₂ = не задовольняє

iзопериметричній умові , a задовольняє.

Шукана екстремаль

Приклад 4 . Знайти екстремалі ізопериметричної задачі

J[у(х)] = при умовах .

Розв’язання . Розглянемо рівняння Ейлера для допоміжної функції H=P-λG=

=(y')²+x ²- λy².

Звідси , а допоміжні умови приводять до системи рівнянь

Значить , c₁=0 , і .

Знайти допустимі екстремалі в ізопериметричних задачах:

11. у'²d х, у(0) = 0, у(1) = 2, у²dх = 4.

В.у =

12. у₁ 'у'₂ dx, у(0) = (0,0) у(1) = (1,2), у₁ dx = 0, y₂dx = 0.

В. у₁ =3х²-2х, у₂ = 6х²-4х.

13. (y ₁'²y'₂²)dx ,у(0) = (0,0) у(1) = (0,0), у_Іу₂dх = -2.

В. у₁ = 2sin kπх, у₂= -2sin kπх, k = 0, ±1, ±2,...

14. Знайти екстремалі в ізопериметричних задачах :

а) J[у(х)] = ; y(0)=0, y(1)=0 при умові

B . y=-12(x²-1) – min.

б) J[у(х)] = y(0)=1, y(1)=0 при умові

B. y= -15x²+14x +1 - min.

в) J[у(х)] = y(0)=y(π)=0 при умові (вважати x<0) .

B. y= - min.

15. Знайти екстремалі в ізопериметричної задачі :

J[у(х)] = при умовах

B. y = де визначаються з граничних і ізопериметричних умов .

16. Знайти диференціальне рівняння для екстремалей ізопериметричної задачі про екстремум функціонала

J[у(х)] = при умові

B.

Тривіальний розв’язок у(х)=0 не задовольняє ізопериметричну умову , а нетривіальний розв’язок існує лише тоді , коли - λ власне значення оператора .

L[y]=

17. Знайти тіло обертання найбільшого об’єму з даною бічною поверхнею.

В. Тіло обертання кругового сегмента навколо хорди.