§4. Друга варіація функціоналу.

Означeння. Функціонал J[х,у] від двох змінних х, у які належать деякому лінійному простору називається білінійним, якщо при фіксованому х він лінійний по у, а при фіксованому у - лінійний по х.

Якщо в білінійному функціоналі покласти х = у, то одержимо функціонал J[у,у], який називається квадратичним. Нехай J[у(х)] - функціонал, визначений на якому-небудь лінійному нормованому просторі.

Означення. Квадратичний функціонал L₂[δу] називається другою варіацією функціонала J[у(х)] і позначається δ²J = L₂[δу], де

∆J= L₁[δу] +¹/₂ L₂[δу] + β||δу||², тут L₁[δу] - лінійний функціонал, L₂[δу] -квадратичний функціонал, β → 0 при ||δу|| → 0.

Приклад. Знайти другу варіацію функціонала

J[у(х)]= , визначеного на просторі С⁽¹⁾_{[ 0,1]} функцій у(х).

Розв'язання. Маємо

∆J = J[у + δу] - J[у] = (х(у + δу)² + (y'+δу')³- ху² - у' ³ )dх =

= (2хуδу + х(δу)² +3y' ²δу'+3у^'(δу')² +(δу')³)dх =

= (2хуδу + 3у' ² δу')dх + (х(δу)² +3у' (δу' ²)dх + (δу')^г dх.

При фіксованому у(х) перший доданок правої частини є лінійний відносно δу(х) функціонал; другий доданок правої частини є квадратичний функціонал, а третій - допускає оцінку

Це значить, що цей доданок представляється у вигляді , де β→0 при ||δy||→ 0. Отже, цей функціонал має другу варіацію δ²J:

Введемо функцію Ф(α) = J[у + αδу]. Друга варіація функціонала визначається також через другу похідну функції Ф(α) в точці α = 0:

або

Задачі: Знайдіть двома способами другу варіацію функціоналів.

1. J[у(х)]=

2. J[у(х)]=

3. J[у(х)]=

4. J[у(х)]=

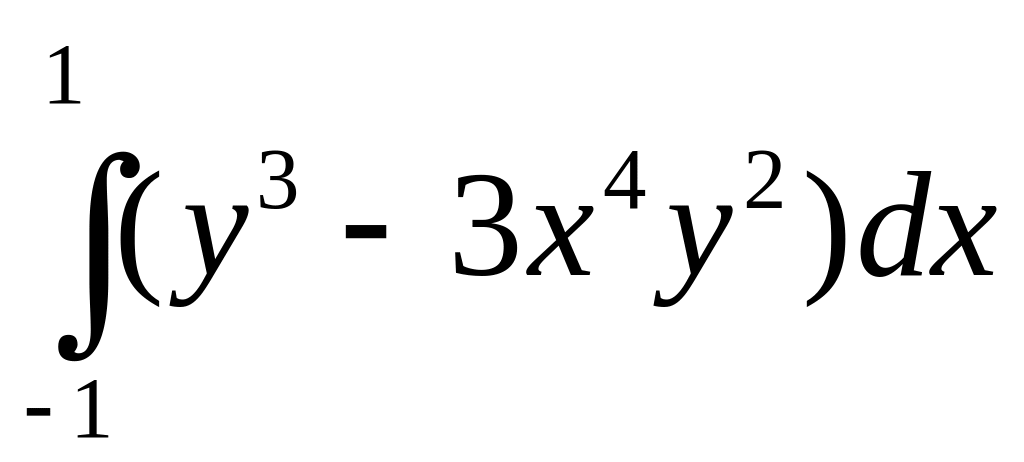
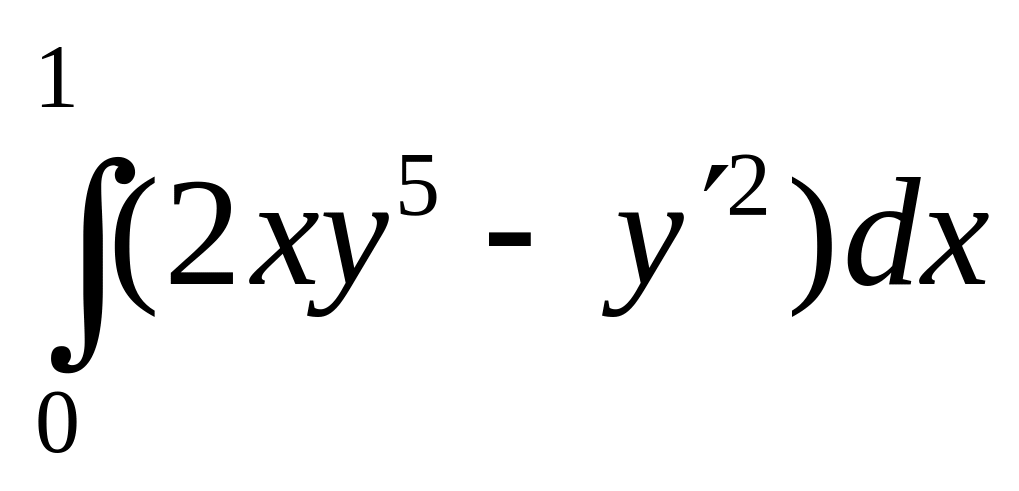
5. J[у(х)]=

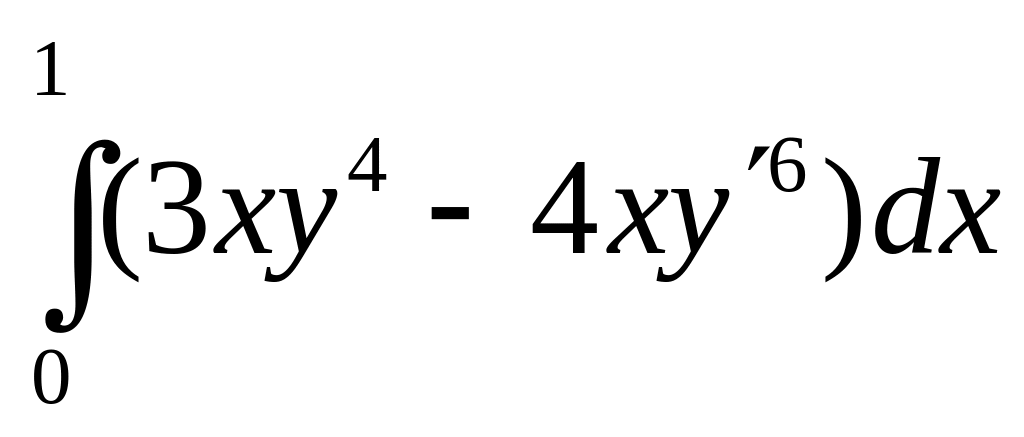
6. Довести, що квадратичний функціонал диференційований і знайти йогo другу варіацію. (В. δJ²(у, у) = 2J[δу, δу]).

§5. Екстремум функціоналу.

Найпростіша варіаційна задача.

Екстремалі функціоналу J[у(х)] = F(х ,у, у')dх.

Функціонал J[у(х)] приймає на кривій у = y_о(х) максимум, якщо значення функціоналу на будь-якій кривій близькій до у = у_о(х) кривій не більше,

ніж J[у_о (х)], тобто:

∆J= J[у(х)] -J[у₀(х)]≤0.

Якщо ∆J ≤ 0, причому ∆J = 0 тільки при у(х) = y_о(х), то на кривій у = y_о(х) досягається строгий максимум, (мінімум для функціоналу буде тоді,

коли ∆J ≤ 0).

Приклад 1.

Показати, що функціонал

J[у(х)] = (х² + у^г)dх на кривій у = 0 досягає строгого мінімуму.

Розв'язання.

Для будь-якої неперервної функції у(х) на [0; 1] маємо

∆J = J[у(х)] – J[0]= (х^г+у^г)dx - х² dх = у²dх ≥ 0, причому знак

рівності досягається лише при у(х) ≡ 0.

Розглянемо функціонал J[у(х)] = F(х,у,у')dх (1).

Задача знаходження екстремуму цього функціоналу на множині

G= {у(х)| у(х) С' [х₀, x₁], у(а) = у_о, у(b) = у₁}називається найпростішою задачею варіаційного числення. В цій задачі звичайно уточнюють поняття екстремуму. Якщо функціонал J[у(х)] досягає на кривій у = у_о(х) екстремум по відношенню до всіх кривих у(х) G, близьких до у_о(х) тільки по ординаті (близькість кривих в смислі нульового порядку), то екстремум називається сильним, а якщо враховується близькість кривих і по ординатах, і по напрямку, то екстремум називається слабким, (близькість кривих розуміється в смислі першого порядку).

Приклад 2.

Нехай маємо функціонал J[у(х)] = у²(1-у' ²)dх в просторі функцій у(х)

= С⁽¹⁾[0; π] з граничними умовами у(0) = 0; у(π) = 0. Відрізок у ≡0, х [0; π ] дає слабкий мінімум функціоналу J. Дійсно, для у = 0, J= 0, а для кривих у(х), всі близькі до у = 0 в смислі близькості першого порядку |у'| < 1, то підінтегральний вираз додатній при у ≠0, і J додатній і перетворюється в 0 лише при у ≡ 0. Отже, при у ≡ 0 х [0; π] досягається слабкий мінімум.

Сильний же мінімум не досягається. Щоб це показати покладемо

тоді

і при n достатньо великому буде J < 0.

З другого боку, всі ці криві при п достатньо великому, близькі до у ≡0 в смислі близькості нульового порядку. Отже, сильний мінімум не досягається при у = 0.

Приклад 3.

Розглянемо функціонал

J[у(х)] = x² у' ²dx, у(-1) = -1; у(1) = 1.

Маємо J[у(х)] ≥ 0 на [-1; 1] і J[у(х)] = 0 тільки при у' = 0, тобто у(х) = с. Функції у = с С⁽¹⁾ [-1; 1], що мають на [-1; 1] неперервну похідну першого порядку, але не задовольняють заданим граничним умовам. Значить, J[у(х)] > 0 для всіх у(х) С⁽¹⁾ [-1; 1], що задовольняють умовам у(-1) = -1, у(1) = 1.

Таким чином функціонал має нижню грань, але вона не досягається на кривих у(х) С^(І)[-1; 1]. Дійсно, розглянемо сім'ю кривих

a>0 .

Ці криві задовольняють граничні умови: у(-1) = -1, у(1) = 1. При а → 0 одержимо граничну функцію

Ця функція кусково - диференційовна на [-1; 1].

Маємо

J[у(х)]=

Звідси слідує, що J[у(х)] → 0 при а →0. На граничній функції у(х), яка задовольняє граничним умовам у(-1) = -1, у(1) = 1, функціонал приймає значення нуль. Отже, функціонал J[у(х)] приймає свій мінімум на кривій

(х) = signx , яка належить до класу функцій кусково - диференційовних на

[-1; 1], але не належить до класу С^(|)[-1; 1].

Необхідна умова екстремуму функціоналу.

Якщо функціонал J[у(х)] досягає екстремуму при у = y_о(х), де у₀(х) -внутрішня точка області визначення функціоналу, то при у = у_о(х) маємо δJ[у₀(х)] = 0.

Далі розуміємо тільки слабкий екстремум. Основою для розв'язання варіаційних задач є твердження:

якщо функція у_о(х) G реалізує екстремум функціоналу (1), то вона є

розв'язком рівняння Ейлера F'_y - F' _y' = 0. (2)

Сім'я інтегральних кривих рівняння (2) у = у(х, с₁ с₂) називається екстремалями функціоналу (1).

Якщо екстремаль належить множині G, то вона називається допустимою. Отже, для знаходження допустимих екстремалей необхідно з системи рівнянь

у(а, c₁, с₂) = у_о, у(b, с_1, с₂) = у₁ виразити с₁ = с₁⁽⁰⁾ і с₂ = с₂⁽⁰⁾. Якщо екстремальне значення функціоналу (1) існує, то воно реалізується функцією

у = у (x, с₁⁽⁰⁾ ,с₂⁽⁰⁾).

Приклад 1.

Знайти допустимі екстремалі функціоналу:

J[у[х)]= (12ху +уy'+у' ²)dх

при умові у(0) = 1, у(1) = 4.

Розв'язання.

Складемо рівняння Ейлера;

, яке приймає вигляд

12х + у' - у' - 2у" = 0, тобто 12х - 2у" = 0.

Значить у" = 6х у = х ³+ c₁ x+ с₂. Підставляючи граничні умови маємо: c₁=2,

с₂ = 1. Таким чином, у = х³ + 2х+ 1.

Відмітимо випадки, коли рівняння Ейлера має перші інтеграли.

1) функція F не містить у: F = F(х, у').

Рівняння Ейлера має вигляд

(*)

Приклад 2.

Знайти екстремалі функціонала

Розв'язання.

З рівняння Ейлера (*) (F не містить у), одержимо ,тобто

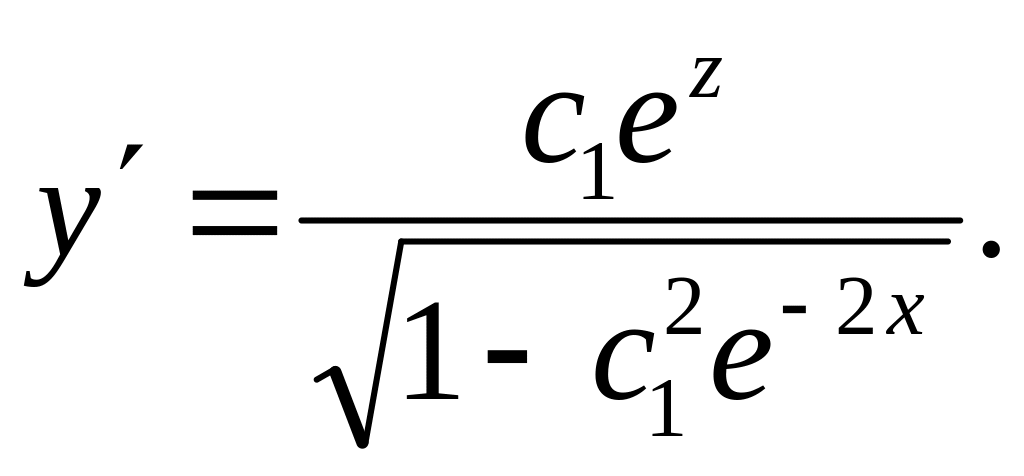
Звідси знаходимо рівняння екстремалей

у = с₂ + агссоs(c₁e^-x ).

2) функція F залежить тільки від у і у':

F = F(у, у'). Тоді рівняння Ейлера має перший інтеграл

(**) F- у' F'_y =с.

Приклад 3.

Серед кривих, які з'єднують дві точки (а, у₀) і (b, у₁), знайти ту, яка при обертанні навколо осі Ох утворює поверхню найменшої площі.

Розв'язання.

Площа поверхні обертання кривої у(х) навколо осі Ох визначається іінтегралом

S(у) = 2π

Для підінтегральної функції рівняння Ейлера (F не містить х) має вигляд

(**), що , тобто у = Звідси

, тобто у = . Сталі c₁ і с₂ визначаються з рівнянь

Приклад 4. Знайти екстремалі функціонала

Розв’язання . не залежить від х , то замість рівняння Ейлера розглядаємо перший інтеграл

:

Значить , . Скористаємось далі крайовими умовами

y(-1)=y(1)=b>0. Для знаходження c і c₁ маємо систему

При b<1 ця система розв’язків немає , при b=1 одержуємо c²= і , а при b>1 - c²= або .

Отже , якщо b<1 , то дана варіаційна задача екстремалей немає , при b=1 є одна екстремаль , а при b>1 - дві (в останніх випадках екстремалями є параболи ).

Приклад 5.Проаналізувати екстремальні задачі для функціоналів :

а)

б)

в)

Розв’язання . Оскільки

а) б) в) , то відповідні рівняння Ейлера мають вид

а)0=0 , б) y'-y' =0 , в) xy'-(xy)'=0

тому в перших двох випадках значення функціоналів не залежить від вибору функції у , що задовольняють умовам (y(0)=0,y(1)=1).

В випадку в) y(x)≡0 і , значить , y(1)≠1 . Значить екстремуму немає .

Зауваження . Те ,що в перших двох випадках значення функціоналів не залежить від вибору функції y(x), ясно і безпосередньо оскільки

.

Приклад 6. Знайти сім’ю екстремалей функціонала .

=

Розв’язання . Перший інтеграл рівняння Ейлера має вигляд Щоб про інтегрувати одержане рівняння, покладемо . Тоді , а і . Виключаючи t , одержимо , де - сім’я області з центрами на осі ординат .

Зауваження . Якщо вважати , що деякі точки переміщуються по кривій y=y(x) зі швидкістю V=x , то і .

Значить , значення розглядуваного інтеграла – це час, який витрачається на переміщення по кривій з точки (a,y(a)) до точки (b,y(b)).

Приклад 7. Знайти екстремаль і дослідити на екстремум функціонал

= , визначивши знак його приросту .

Розв’язання . . Відповідне рівняння Ейлера має вигляд , звідки після інтегрування одержуємо . Оскільки і y(-1) =2 , то єдиною екстремаллю даного функціонала є крива

Визначимо знак приросту функціонала в класі функцій на C¹_[-2;-1], що задовольняє вказаним крайовим умовам :

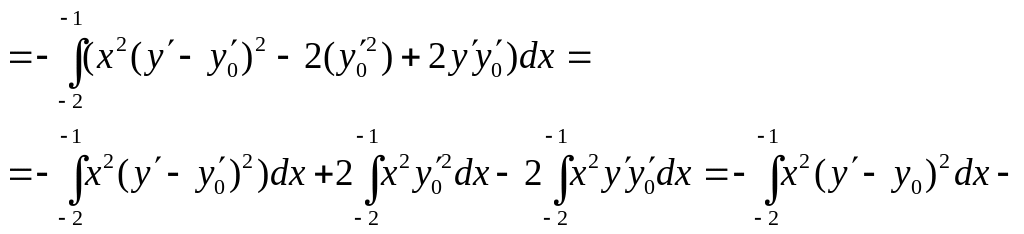
(тут враховано ,що ).

Значить , розглядуваний функціонал досягає на кривій слабого максимуму .

Приклад 8. Дослідити на екстремум функціонал :

Розв’язання . . Рівняння Ейлера приймає вигляд . Враховуючи початкові умови маємо . Шукаємо екстремаль y=Bx.

Розглянемо тепер умови Лежандра і Якобі . Маємо (підсилена умова Лежандра виконується і , очевидно Q=0, а P=6B) . Тому рівняння Якобі має вигляд - - загальний розв’язок цього рівняння , а з врахуванням умов h(0)=0 і маємо h(x)=x. Оскільки h(x) при , то виконується також підсилена умова Якобі .

Отже , на кривій y=Bx даний функціонал досягає слабого мінімуму.

Приклад 9. Дослідити на екстремум функціонал

Розв’язання. Розглянемо спочатку відповідне рівняння Ейлера . Розв’язки його . Екстремаллю даної варіаційної задачі є крива

, де сталі c₁ і c₂ визначені з умов

Далі скористаємось теоремою .

Теорема. Нехай функції неперервні на [a ,b ] і , крім того ,p(x)>0,q(x)≥0 . Якщо y₀ (x) є екстремаль функціонала

і задовольняє умовам y(a)=A, y(b)=B , то на ній реалізується мінімум цього функціонала .

Оскільки p(x)≡1>0,q(x) 1>0 , а , то на основі цієї теореми на кривій y₀ реалізується мінімум.

Приклад 10. В просторі C¹_[-1;1] дослідити на екстремум функціонал

J[y(x)]= .

Розв’язання. Знайдемо екстремалі даної варіаційної задачі . Оскільки функція не залежить від у , то рівняння Ейлера має вигляд , або . Однак функція у(х) має належати простору C¹_[-1;1] , тому необхідно c₁=0.

Можливі два випадки:

а) Якщо А=В, то шуканою екстремаллю є функція y₀(x)≡A. Очевидно, що в цій точці функціонал J досягає мінімуму , оскільки J[y]≥0 C¹_[-1;1] і J[y₀]=0.

б) Якщо А≠В , то екстремалей немає . Значить , даний функціонал не має в C¹_[-1;1] і екстремуму .

Відмітимо , однак , слідуюче.

Розглянемо послідовність функцій

, що задовольняють початкові умови і належать простору C¹_[-1;1] , бо . Тоді для довільного маємо

Значить , . Це означає, що хоча J[y]>0 C¹_[-1;1], y(-1)=A, y(1)=B, але int J[y(x)]=0 .

Приклад 11. Дослідити варіаційну задачу для функціонала

при умові . Вважається , що функції M , N, визначені і неперервні в області [a;b]x .

Розв’язання. Не будемо приводити необхідні і достатні умови екстремуму функціонала .

Відомо , що вираз M(x,y)dx +N(x,y)dy при вказаних умовах є повним диференціалом . Значить , інтеграл

не залежить від шляху інтегрування , а варіаційна задача для розглядуваного функціонала не має смислу .

Приклад 12. Серед всіх ліній , що з’єднують точки (-1, ch1) і (1, ch1 ) знайти ту , яка при обертанні навколо осі х утворює поверхню з найменшою площею .

Розв’язання. Шукана площа поверхні обертання виражається інтегралом

.

Тому це задача про мінімум функціонала

Запишемо перший інтеграл рівняння Ейлера

.

Якщо врахувати початкові умови , то одержимо екстремаль y₀(x)=chx . З геометричних міркувань слідує, що даний функціонал на цій кривій досягає мінімуму.

Задачі.

Серед неперервно диференційовних на [а; b] функцій знайти екстремалі функціоналів.

1. J[у(х)]= (у+ , 0<а<b.

B.y= .

2. J[у(х)]= (у + 2.xy'+(y')²)dх, у(0) = у₀ у(1) = y₁ В.у = -- х²+(y₁ - у₀+ )х + y₀

З. J[у(х)]= ((у')² -4у²)dx, В.у = c сos(2х + c₁).

4. J[у(х)]= ((e^2у +2(у')²)dх, В. у = lnc -lnсоs(сх + с₁).

5. J[у(х)]= dx, В.у = sh(с,х+.с_г).

6. J[у(х)]= (х²у' ² + 2y²+ 2хy)dx, В.у = с₁х + + хln|x|.

7. J[у(х)]= , В. .

8. J[у(х)]= (x²y' ²+12y²) dx, 0<а<b. В. с₁ х³+

9. J[у(х)]= (у + 2ху'+у'²)dx , у(0) = 1;y (1) = 2. В. у(х) = [0;1].

10. J[у(х)]= (12xу + yу'+y' ²)dx B. y = х³ +с₁ х + с².

11. J[у(х)]= 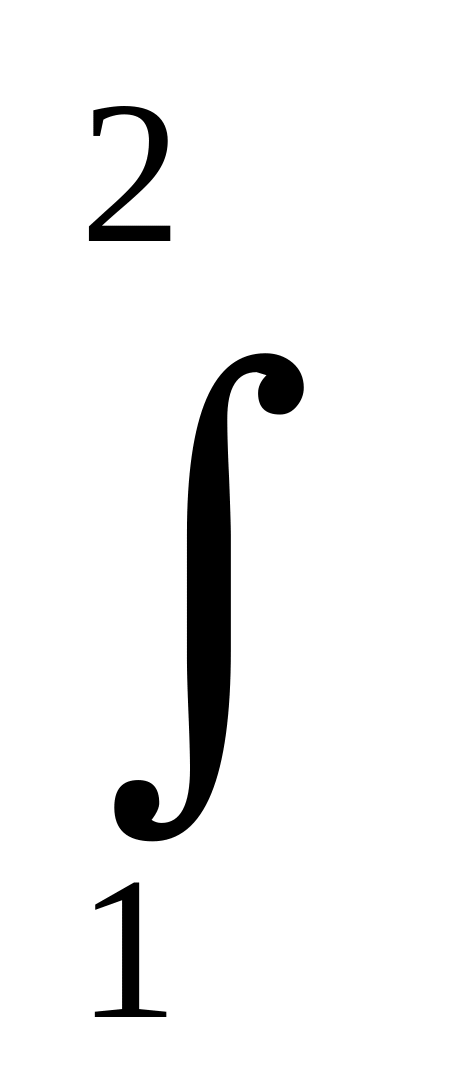(у'²+2уу^'+ 16у² )dх, В.у = с₁е^-4x +с₂е^4х.

12. J[у(х)]= (у'²-4у²)dx, В. у = с₁ sin 2х + с₂ соs 2х.

13. J[у(х)]= , В. у = tg(с₁ х + с₂).

14. J[у(х)]= (у² - у'²-2усоsх)dх, В. у = хsinх + с₁ sinх + с₂ соsх.

15.J[у(х)] = (2xу'- у'²)dх, у(-1) = 0, у(1) = В.у = х^г-

16.J [у(х)] = (у² + 2хуу')dх у(х₀) = y_o, у(x₁`) = y₁

В. Інтеграл не залежить від шляху інтегрування (повний диференціал під інтегралом). Варіаційна задача не має смислу.

17.J[у(х)]= (xу+у²-2у²у')dх, у(0)=1, у(1)=2; В. В класі неперервних функцій екстремум не досягається.

18. J[у(х)] = у'(1 + х²у')dх B..у= + с₂.

19. J[у(х)] = (у' ² + 2уу' -16у²)dх В. у = с₁ sin(4х-с₂).

20. J[у(х)] = (ху'+ у' ²)dх В. у = - с₁х + с₂.

21. J[у(х)] = (у² + у' ² - 2у sinx) dх В. у = с₁е^х + с₂е ^х + sinх.

22. J[у(х)] =

23. J[у(х)] = В. у = с₁x⁴ +с₂.

24. J[у(х)] = (у² +у' ² +2уе^х)dх В. у = хе^х +с₁е^х +с₂ e ^-х.

25. J[у(х)] = ( у² +у' ² +2уsinx)dх В. у = - + с₁соsх + с₂sinx.

26. J[у(х)] = (у² +у' ² + )dх В. у = с₁ch х + с₂shх + хshх-сhх ln сhх.

27 J[у(х)] = (2ху + (х² + е^у)у')dх, у(а) = А, у(b) = В.

В. Інтеграл не залежить від шляху інтегрування (повний диференціал під

інтегралом). Варіаційна задача не має смислу. 28. J[у(х)] = (е^у + ху')dх, у(0) = 0 у(1) = а.

В. у = 0, якщо а = 0; при а ≠ 0 гладкої екстремалі немає.

29. J[у(х)] = (у' ² - у² ) dх, у(0) = 1, у(π / 4) = В. у = соsх.

30. J[у(х)] = (х + у'²)dx ,у(0)=1,у(1) = 2В.у = х+1.

31. J[у(х)] = (у² + у'²)dх, у(0) = 0, у(1) = 1 В. у =

32. J[у(х)] = (у'² + 4у²)dх, у(0) = е^х, у(1) = 1 В. у = е^2(1-x).

33.J[у(х)] = (2е^у –y²)dx, у(0) = 1, у(1) = е.

В. Немає екстремалей; рівняння Ейлера немає розв'язків. 34. J[у(х)] = (ху' + у^'2)dх, В. у = с₁+с₂х- .

35. Довести, що лінійний функціонал

J[у(х)] = (p(х)y' + q(x)y + r (х))dx , де р(х), q(x), г(х) С_[а,_b] немає

екстремумів.

Знайти екстремалі функціоналів:

36. J[у(х)] = (у² + у'² + 2уе^х)dх, В. у =c₁e^x + с₂ е ^-x+ хе^х.

37. J[у(х)] = (у² - у'² - 8усhх)dx , у(0) = 2, у(π/2) = 2chπ/2.

В. у = 2сhх.

38. J[у(х)] = х⁴ у' ²dх

39. J[у(х)] = (y'² – y²)dx , у(0) = 1, у(π) = -1

В. у =соsх +csinx, де с - довільна стала.

40. J[у(х)] = х²у' ² dx , у(-1) = -1, у(1) = 1

В. гладких екстремалей немає

41. J[у(х)] =

42. Знайти допустимі екстремалі функціоналів:

a) J[у(х)] = (12xy+yу^' + у'² )dх, В. у =x³+c₁ x+c₂.

б)J[у(х)] = ( у'² + 2уy'+16y²)dх, В. у =c₁e^-4x + с₂ е ^4x.

в) J[у(х)] = (у'² + 4у²)dх, В. у =c₁sin2x + с₂ cos2x.

г)J[у(х)] = dх, В. у =tg(c₁x + с₂ ).

д) J[у(х)] = (у² + у'² + 2уcosx)dх, В. у = xsinx +c₁sinx + с₂ cosx.

е) J[у(х)] = (2xy'- у'² )dх, y (-1)=0,y(1)=

В. у =x² - x- .

43. J[у(х)] = 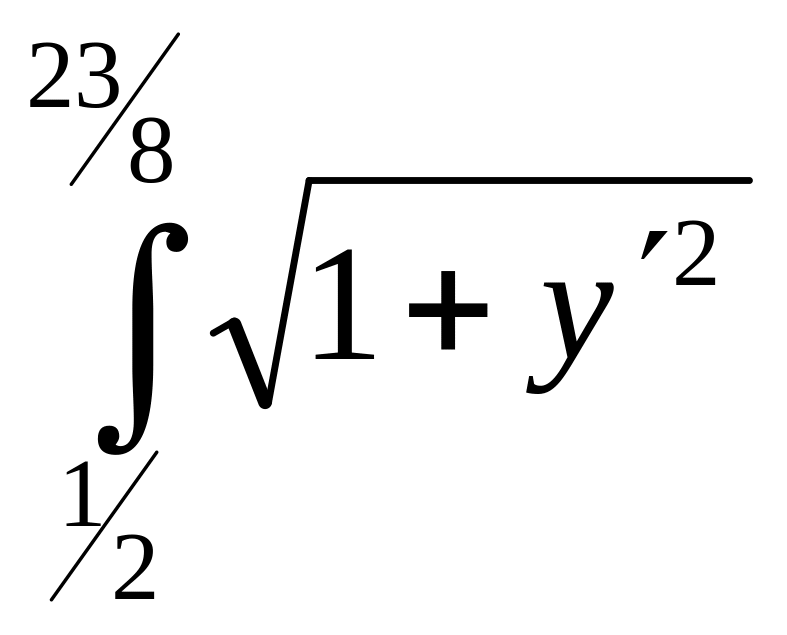dх, при умовах у =x² ; у=х-5.

44. J[у(х)] = (x² у'² + уx)dх, при у =2x-1, y=x².

45. J[у(х)] = (у+ +2xy'+у'² )dх, при у =2x+1, y =-x+2.

46. На яких кривих можуть досягати екстремум слідуючі функціонали:

а) J[у(х)] = ( у'² - у²)dх, у (0)=0, y( )=1

б) J[у(х)] = ( у'² +12x у)dх, у (0)=0, y(1)=1

в) J[у(х)] = dх, у (1)=0, y(2)=1

47. Знайти екстремалі функціоналів:

J[у(х)] = dх, y(a)=A , y(b)=B

B. y= sh (c₁ x +c₂)

48.Довести , що єдиною екстремаллю функціонала

J[у(х)] = dх, у (0)=0, y(1)=1, є лінія у=х

49. Знайти екстремалі слідуючих функціоналів:

a) J[у(х)] = у² dх, у(a) =A, y(b)=B

б) J[у(х)] = ( у²+ x²y')dх, у (0)=0, y(1)=a

в) J[у(х)] = (у+ xу')dх, у(a) =A, y(b)=B

г) J[у(х)] = (у² + у'² - 2уsinx )dх,

В.а) y=0 тільки при A=B=0

б) y=x при a=1 , при a 1 екстремалей немає

в)інтеграл не залежить від шляху інтегрування і варіаційна задача не мах смислу

г) y(x)= c₁e^x + с₂ е ^-x+ sinx.

50.Дослідити на екстремум функціонал

J[у(х)] = ( у'² - у²)dх, у (0)= y(a)=0,

якщо a) 0<a <π ; б) π<a<2π

В.а) min при y=0 .

б) екстремуму немає .

§6. Перше узагальнення найпростішої задачі варіаційного числення. Екстремалі функціонала J[у(х)] = F((х,у,у',у",...,у⁽ⁿ⁾)dх .

Нехай маємо функціонал J[у(х)] = F((х,у,у',у",...,у⁽ⁿ⁾)dх при граничних

умовах: у(х₀) = у₀, y'(х_о) = у'_о, …, y^(,n-1) (х_о) = y^{(,n -1)} (х_о)

y(х₁) = у₁,у'(х₁) = у'_1, ..., y^(,n-1) (х₁) = y^(,n-1) (х₁).

Функція F - диференційовна n+2 рази по всіх аргументах, у(х) С⁽²⁾ [х₀,x₁]. Екстремалями функціонала є інтегральні криві рівняння Ейлера-Пуассона:

Серед розв'язків цього рівняння, якщо вони існують, є екстремалі функціонала.

Приклад. Знайти екстремаль функціонала.

J[(х)]= (360х²у-у"²)dх,

у(0) = 0; у'(0) = 1; у(1) = 0; у'(1) = 2,5.

F = 360х²у-y"²-

F'_у = 360х²; F'_У' = 0; Р'_{у' '} = -2у".

Рівняння Ейлера-Пуассона має вигляд:

360х² + (-2y'') = 0 або 360х² - 2у = 0;

і т.д.

Загальний розв'язок

Використовуючи граничні умови, маємо:

c₁ = ; с₂ = -3; с₃ = 1; с₄ = 0.

Шукана екстремаль у =

Задачі. Знайти екстремалі функціоналів:

1. J[у(х)]=

y(0)=0 ; y' (0)=1;

y(1)=0 ; y' (1)=-sh1; B.y(x)=(1-x)sh1.

2. J[у(х)]=

y(-1)=1 ; y' (-1)=4,5; y''(-1)=16;

y(0)=0 ; y' (0)=0; y''(0)=0; B.y=

3. J[у(х)]=

y(a)=y₀ ; y' (a)= y'₀ (x);

y(b)=y₁ ; y'(b)=y'₁. B. Екстремуму нема.

4. J[у(х)]=

y(а) = А_1; y'(a) = A₂;

y(b) = B_1; y'(b) = B₂;

В. Варіаційна задача не має смислу бо під інтегралом є повний диференціал

функції уу".

5. J[у(х)] = (у'²+у" ²)dх,

у(0) = 0; у'(0)=1;

у(1) = sh1; у'(1) = сh1. В.у(х) = shх.

6. J[у(х)] = (у")² dх, у(а) = 0; у'(а) = 1; у(b) = 1; у'(b) = 1.

7. J[у(х)] = (y'')² dx,у(0) = 0;у'(0) = 0;у(1) = 2;у'(1)=1.

Приклад 2. Знайти екстремалі функціоналу.

J[у(х)]= (16у²-у'²+е^x)dх.

Розв 'язання. Складаємо рівняння Ейлера-Пуассона: 32у —2у ^IV =0. Звідси маємо: Задачі. Знайти екстремалі функціоналів.

8 .J[у(х)] = (4y² + 5y' ² + y"² )dx , В. у = с₁ е^х + с₂е ^-х + с₃е^2х +с₄е ^{- 2х}.

9. J[у(х)] = (2xy + y'"²)dx ,у(0) = у'(0) = у"(0) = у(1) = у'(1) = y"(1)=0

В. у = (х⁷ - 6х⁵ + 8х⁴ - 3х³).

10. J[у(х)] = (4y²-5y'²+y''²)dx . у(0) = 3; у'(0) = 4;

у(π/2)=1; у'(π /2) = -4. В. у = 2соsх + 2sinх+соs2х + sin2х.

11. J[у(х)] = (уу' + у'² + уу" + у'у" + у"²)dх. В. у = c₁+ c₂x + c₃x² +c₄x ³. .

12. J[у(х)] = (16у² - у"² + х²)dx.

B. у = c₁ e^2х + с₂е ^{- 2х} + с₃соs2'x +с₄sin 2х.

13. J[у(х)] =

В. у = (c₁+ c₂x)cosx + (c₃ + c₄x)sinx -

14. J[у(х)] = (y'"² + у² - 2ух³)dх.

В. у = с₁ е^х + с₂е ^-х + (с₃ соs х + с₄ sin х) +

+ (с₅ соs х + с₆sin х) + х³ .

15. J[у(х)] = (1 + у"²)dх; у(0) = 0; у'(0) = 1; у(1) = 1; у'(1) = 1.

16. J[у(х)] = (у" -у²+ х²)dх; у(0) = 1; у'(0) = 0; у(π/2) = 0; у'(π/2)=1.

17. J[у(х)] =

18. J[у(х)] =

19. J[у(х)] =

B.y=