§14. Необхідні достатні умови мінімуму (максимуму) функціонала

J[y(х)] = F(х,у,у ' )dx .

Слідуючі твердження дають необхідні і достатні умови мінімуму функціонала J[y(х)] на множині G.

Для того, щоб допустима екстремаль у(х) давала мінімум функціоналу J[у(х)], необхідно, щоб

а) 0 для всіх х [а; b] - (умова Лежандра);

б) на інтервалі (а; b) не було спряжених точок (умова Якобі) (екстремаль включається в центральне поле екстремалей)

і достатньо, щоб

в) 0 для всіх х [а; b] - (посилена умова Лежандра);

г) на (а;b] не було спряжених точок (умова Якобі) (екстремаль включається в центральне поле екстремалей)

Для одержання необхідних умов і достатніх умов максимуму функціоналу J[y(х)] на множині G нерівності, які фігурують в цьому твердженні, слід замінити на обернені.

Приклад 1. На множині G = {у(х)| у C ⁽¹⁾ (0, Т), у(0) = 0, у(Т) = у₁}

дослідити на екстремум функціонал J[y(х)] = (у² - у' ²)dх.

Розв'язання. Рівняння Ейлера має вигляд у" + у = 0. Допустимою,

екстремаллю є у(х) = при Т , якщо ж Т = і у₁ 0, то

допустимих екстремалей немає. Рівняння Якобі u" + u = 0 має розв'язок

u(х) =sinх (при початкових умовах u(0) = 0, u'(0) = 1). З точкою х = 0 спряжена точка х = π. Значить, при Т< π умова Якобі виконується, а при Т > π - ні. Оскільки = -2 < 0, то виконується підсилена умова Лежандра. Отже, якщо

0 < Т < π, то функція у(х) = дає максимум функціоналу J[y(х)] .

При T > π екстремуму немає.

Задачі. Дослідити на екстремум функціонали:

1. J[y(х)] = (у' ²+3у²)е^2хdх, у(0) = 0, у(ln2) = 15/8.

В.у(х) = e^x – е^{- 3x} —min.

2. J[y(х)] = (у'² + у²-4уsin х)е^2x dх, у(0) = 0, у(Т) = у₁.

В. у(х) =

3. J[y(х)] = х²у' ² dх, у(1) = 3, у(2)= 1.В.у = 4/х- 1-min.

4. J[y(х)] = (2ху- у'²)dх, у(0)=1,у(6)=1.В. у = + 6х + 1-mах.

Приклад 2. Дослідити на екстремум функціонал J[y(х)] = (1 + х)у'²dх,

у(0) = 0,у(1)=1.

Розв'язання. F(х,у,у') = (1 + х)у' ²; рівняння Ейлера F_y' - = 0;

F_y'= 0; = 2y'(1 + х)) має вигляд (1+х)у" + у' = 0.

Розв'язуючи це рівняння, знаходимо екстремалі: у'(х) = р(х); (1 + х)р' + р(х)=0;

; ; ;

у(х) = с₁ 1n |1 + х | +с₂ - екстремаль.

Знаходимо екстремаль, яка задовольняє граничним умовам:

у(0) = 0; у(1) = 1.

Знаходимо F''_yy = 0; = 0; = 2(1 + х), на даній

екстремалі

Відповідь: на екстремалі у = досягаєтся сильний мінімум.

Використовуючи достатні умови, дослідити на екстремум функціонали:

1. J[y(х)] = (у²-у'²)dх, у(0) = 0, у(Т) = 2.

В. ; 0<T<π.

2. J[y(х)] = х²у'²d х, у(1) = 3;у{2) = 1. В.у = 4/х-1.

3. . J[y(х)] = (2ху-у'²)dх,у(0)=1;у(6)=1.В. у = + 6х + 1- max

4. J[y(х)] = y'³ dx, у(0) = 0, у(3) = 6. В. у = 2х - min.

5. J[y(х)] = уу'²dх, у(0) = 5,у(1) = 5. В. у = 5 -слабкий min. Знайти екстремалі в слідуючих ізопериметричних задачах,

6. J[y(х)] = (х + у' ^г)dх, у(0) = 0, у(1) = 0 при умові у(х)dх = 2.

В. у = - 12(х²- 1)-min.

7. J[y(х)] = (х² + у'²)dх,у(0)=1,у(1) = 0 при умові у(х)dх = 2.

В. у = - 15х²+ 14х+1 -min. .

8. J[y(х)] = у'²dх, у(0) = у(π) = 0 при умові у²(х)dх = 1(вважати λ< 0).

В. у = ± sinх-min.

Приклад 3. Дослідити на екстремум функціонал J[y(х)] = (у' - αу')dх,

у(0) = 0, у(1) = -2( ).

Розв'язання. Оскільки підінтегральна функція залежить лише від у', то екстремалями є прямі у = с₁ x + c₂. Екстремаллю, яка задовольняє граничні умови, є пряма у = -2х, яка може бути включена в центральне поле екстремалей у = сх. . На цій екстремалі нахил поля р = -2. Знаходимо , = 6у'. На даній

екстремалі маємо, що = —12 < 0, тобто на лінії у = - 2х достатньо слабкий максимум функціоналу. При довільних значеннях у' знак , не зберігається, отже, достатні умови сильного максимуму не виконуються.

Приклад 4. Дослідити на екстремум функціонал J[у(х)] = (е ^у' +3)dх,

у(0) = 0;у(2)=1.

Розв'язання. Екстремалями є прямі у = с₁ x + c₂. Екстремаллю, яка задовольняє граничним умовам є пряма у = х/2; вона може бути включена в центральне поле екстремалей у = сх. В даному випадку (х,у,у') = е^у' > 0

для будь-яких значень у'. Значить на екстремалі у = х/2 функціонал має сильний мінімум.

Приклад 5. Дослідити на екстремум функціонал J[y(х)] = ,

у(0) = 0;у(а) = у₁.

Розв'язання. Підінтегральна функція не залежить явно від х, значить,

одержимо F—y' =с₁, що дає: звідки

, або у(1 + у'²) = с₁, де с₁ = . Покладемо y' = ctg . Будемо мати у = с₁ sin² = (1 -соst). Далі,

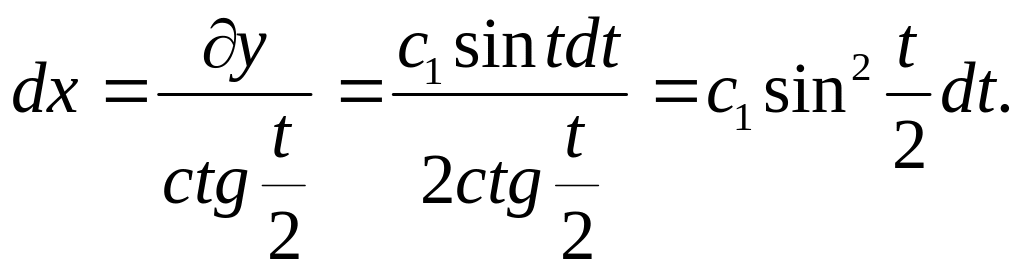Інтегруючи, одержуємо:

. Отже,

—параметричні рівняння сім ї циклоїд.

З умови у(0) = 0 знаходимо, що с₂ = 0. Пучок циклоїд

утворює центральне поле з центром в точці О(0;0), яке включає екстремаль

, де R визначене з умови проходження циклоїди через другу

граничну точку В(а; у₁), якщо а < 2πR.

Використовуючи умову Лежандра , маємо = 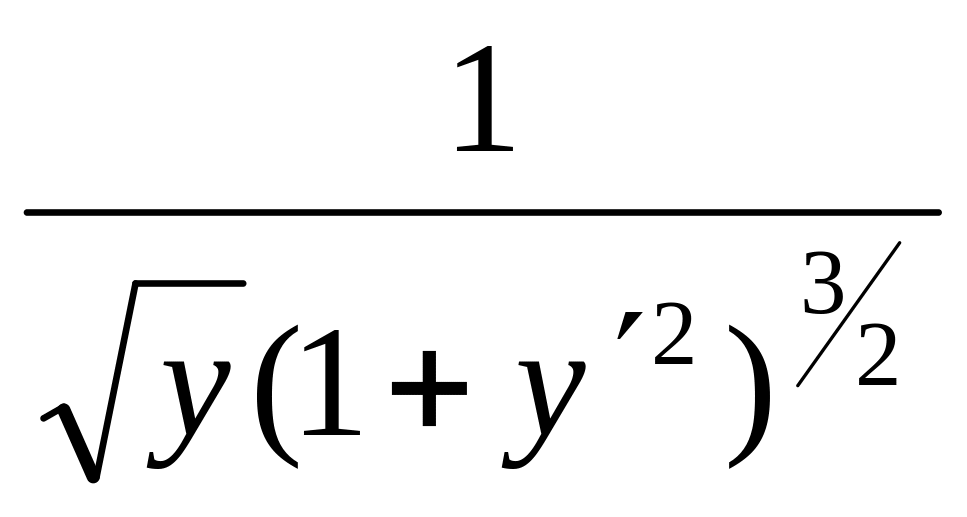>0 для

будь -яких значень у'. Значить, для а < 2πR на циклоїді даний

функціонал має сильний мінімум.

Приклад 6. Перевірити , що функціонал

J[у(х)] = , y(-1)=0 , y(1)=2 , досягає свого мінімуму на кривій

не належить простору C¹[-1;1].

Розв’язання . Сформульоване твердження очевидне , оскільки J[у(х)] ≥0, y і J[у₀] =0.

Цікавим тут є слідуючий факт . Легко бачити , що

(виконується умова Лежандра ) і , тобто розривна екстремаль задовольняє рівняння Ейлера . Якщо є шукати екстремум даного функціонала в класі функцій з C¹_[-1;1] , які задовольняють умовам y(-1)=0, y(1)=2 , то з рівняння Ейлера слідує , що y²(1-y'²)= c₁ , або після відокремлення змінних , інтегрування і врахування початкових умов , маємо y₁ (x)=x+1. Оскільки

J[у(х)] =0 , то на кривій y = y₁ (x)функціонал має слабкий мінімум .

Задачі. Використовуючи умову Лежандра дослідити дані функціонали на екстремум:

9. J[y(х)] = (y²+х²)dx ,у(0) = -1;у(1)=1.

В. у = 2х — 1 — min сильний. .

10. J[y(х)] = (ху' ⁴ -2уу' ³)d х ,у(1) = 0, у(2) = 1.В. у = х² - 1 – сильний min.

11. J[y(х)] = (ху' ⁴ - 2уу' ³)dх, у(1) = 0, у(2) = 1. В. у = х - 1 - слабкий min.

12. J[y(х)] = (1 – е^{-y ' ²} )dx , у(0) = 0, у(а) = b,

В. При | b |< на екстремалі у = х є слабкий min, а при | b |> -

слабкий mах. При |b|= - екстремуму немає.

13. J[y(х)] = yy'²dx ,у(0) = р>0;у(1) = q>0.

В. На екстремалі при р q досягається слабкий

min ; при р = q екстремаллю є пряма у = р — слабкий min.

14. Дослідити на екстремум функціонал J[y(х)] = ( у' ² + у² + х²) dх,

у(0) = 0, у(1) = 1 . При різних значеннях параметра .

В. а) при > 0 екстремаль у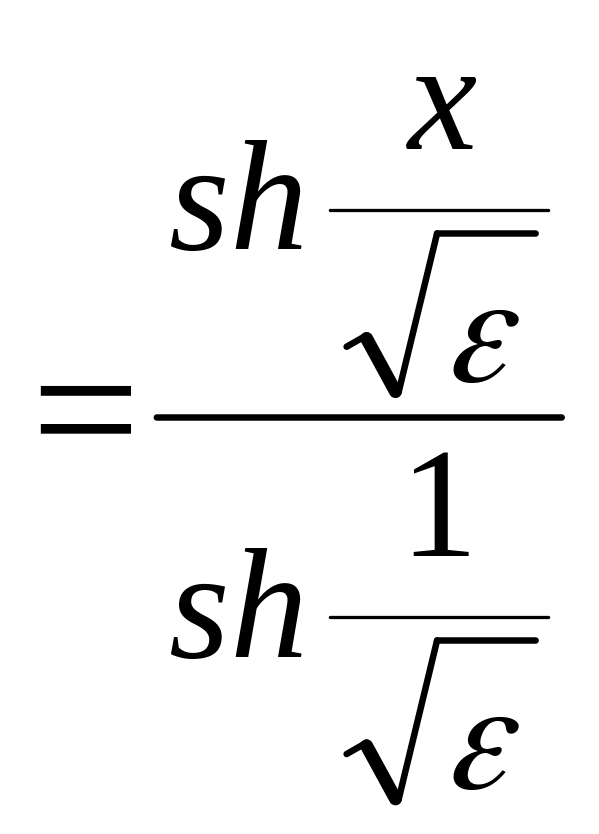

реалізує сильний min.

б) при < 0, | | > екстремаль у реалізує функціоналу

сильний mах.

в) при ε= 0 розв'язок екстремальної задачі в класі неперервних функцій не існує.

Достатні умови Вейєрштраса.

Функція Вейєрштраса визначається рівністю Е(х,у,р,у') = F(х,у,у')-F(х,у,р)-(у'-р)F'_р(х,у,р), де р = р(х, у) - нахил поля екстремалей варіаційної задачі (1)

J[у(х)]= F(х,у,у')dх,(2)у(х₀) = у₀,, у(х₁) = у₁ в точці (х, у).

Достатні умови слабкого екстремуму:

Крива С реалізує слабкий екстремум функціоналу (1), якщо:

1. крива С - екстремаль функціоналу (1) (є розв'язком рівняння Ейлера).

2. Екстремаль С може бути включена в поле екстремалей (виконується умова Якобі).

3. Функція Вейєрштраса Е(х,у,р,у') зберігає знак в усіх точках (х, у) близьких до екстремалі С, і для близьких до р(х, у) значень у'. Функціонал J[у(х)] буде мати максимум на С, якщо Е ≤ 0, і мінімум, якщo Е ≥ 0.

Достатні умови сильного екстремуму.

Крива С реалізує сильний екстремум функціоналу (1), якщо:

1. Крива С є екстремаллю функціоналу, що задовольняє початкові умови.

2. Екстремаль С може бути включена в поле екстремалей.

3. Функція Вейєрштраса Е(х,у, р,у') зберігає знак в усіх точках (х, у), близьких до екстремалі С, і для довільних значень у'. При Е ≤ 0 - буде mах, а

при Е ≥ 0 - min.

Зауважимо, що якщо в точках екстремалі для деяких значень у' функція Е має протилежні знаки, то сильний екстремум не досягається. Якщо ж це буде і

для близьких до р значень у', то не досягається і слабкий екстремум.

Приклад 7. Дослідити на екстремум функціонал J[y(х)] = (у' ³ + у')dх,

у(0) = 0;у(1) = 2.

Розв 'язання. Рівняння Ейлера має вигляд у'у" = 0, то екстремалями є прямі у = с₁ х + с₂. Екстремаллю, що задовольняє граничні умови є у = 2х. Нахил поля в точках цієї екстремалі р = 2. Екстремаль у = 2х включається в центральне поле екстремалей у = сх з центром в точці О(0;0). Перевіримо виконання умови

Якобі. Рівняння Якобі має вигляд = 0. Але згідно рівняння

екстремалі у = 2х у' = 2. Значить, рівняння Якобі зводиться до виду и"(х) = 0

u(х) = с₁ х + с₂. З умови у(0) = 0 с₂ = 0. Але це є розв'язок u= с₁ х при с₁ ≠ 0,

крім точки х = 0, ніде в нуль не перетворюється, то умова Якобі виконується.

Складаємо функцію Вейєрштраса:

Е(х,у,р,у') = у' ³ + у' - р³ - р-(у' - р)(3р² +1) = (у' - р)²(у' + 2р).

Перший множник невід'ємний для всіх у', а другий - додатній при у', які близькі до 2. Значить, виконуються всі умови існування слабкого мінімуму. Для всіх у' Е не буде більше або рівне 0, бо якщо у' < - 4, то Е < 0. Це значить, що умова сильного екстремуму не виконується (Е не зберігає знаку для

всіх у').

Приклад 8. Дослідити на екстремум функціонал

J[y(х)] = (x + 2у + у' ²)dх, у(0) = о, у(1) = 0.

Розв'язання. Рівняння Ейлера має вигляд у" = 2. Екстремалями є сім'я парабол у = х² + с₁ х + с₂. Екстремаль, яка задовольняє граничним умовам є у= х² - х. Рівняння Якобі: = 0 або u" = 0. Його загальний розв'язок u(х)= с₁ х + с₂. Умова u(0) = 0 дає с₂ = 0, а оскільки u(х) = с₁ х при с₁ ≠ 0 ніде на [0; 1] в нуль не перетворюється, крім точки х = 0, то умова Якобі виконується, і значить, екстремаль у = х² - х можна включити в центральне поле екстремалей з центром в точці О(0;0): у = х² + сх. Функція Вейєрштраса має вигляд

Е(х,у,р,у') = (у' — р)² . Звідси видно, що для довільних значень у' буде

Е = (у' — р)² ≥ 0. Значить, на екстремалі y=х² —х даний функціонал

досягає сильного мінімуму, який дорівнює J [х² -х] = 1/3.

Приклад 9. Дослідити на екстремум функціонал :

f(y)=

Розв’язання. не залежить від х , то з рівняння Ейлера слідує , що , тобто , або

Враховуючи початкові умови , маємо систему для вираження сталих c₁ і c₂:

Значить , якщо c₂=1 , то c₁=-1 , а при c₂=-1 , c₁=1 . Підставляючи знайдені значення c₁ і c₂ в рівняння y= (c₁x+ c₂)² , переконуємося , що екстремуми є тільки параболи y₁(x)=((-1+ )x+1)² і y₂(x)=((-1- )x+1)².

Вивчимо тепер розв’язки відповідних рівнянь Якобі. Оскільки Q= , а P= , то рівняння Якобі приймає вигляд або після спрощень . Тому при

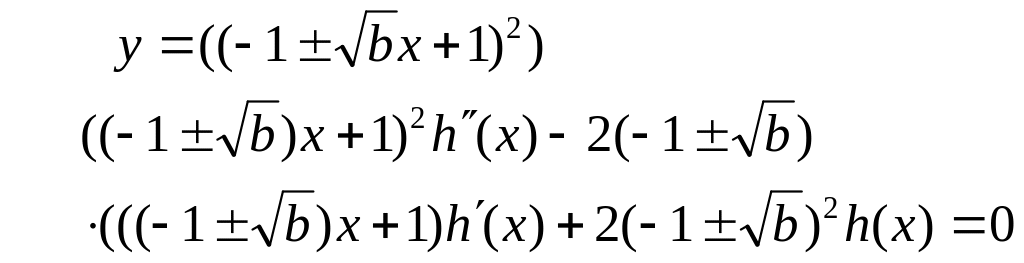
Це рівняння типу рівняння Ейлера . Тому його розв’язок шукаємо у вигляді функцій ((-1 )x+1)^λ. Тоді і для визначення λ одержимо рівняння . Значить і загальний розв’язок вихідного рівняння є :

. Враховуючи початкові умови , одержуємо i . Зауважимо , що функція перетворюється в нуль в точці (0;1) . Значить екстремаль y =y₂(x) не задовольняє одній з необхідних умов екстремуму - умові Якобі. Тому дальшому дослідженню підлягає тільки екстремаль

.

Для неї маємо

а)

б) , тобто виконується підсилена умова Якобі.

Значить на екстремалі функціонал J[у(х)] = досягає слабкого мінімуму Задачі. Дoслідити на екстремум функціонали:

15. J[y(х)] = е^х(у² + у'²)dх ,у(0) = 1,у(1) = е. В. у = е^х - сильний min.

16. J[y(х)] = е^y y'²d х ,у(0) = 0, у(1) = 1n4. В. у = 21n(х+ 1)-сильний min.

17. J[y(х)] = , у(1) = 1, у(2) = 4. В. у = х² - слабкий min.

18. J[y(х)] = ,у(0) = 0,у(а) = b; а> 0,b> 0 .В. у = х -слабкий min.

19. J[y(х)] = (1 + х)у'²dх, у(0) = 0, у(1) = 1. В.у = -

cильний min.

20. J[y(х)] = (у² -у' ²)dх, у(0) = 1, у(π/2) = 1. В.у = соsх + sinх -

сильний mах.

21. J[y(х)] = у'(1 + х²у')dх, у(-1) = 1, у(2) = 4. В. Екстремум на

неперервних кривих не досягається.

22. J[y(х)] = (у'³ + у'²)dх, у(-1) = -1, у(1) = 3.

В. у = 2x + 1 — слабкий min. Сильного екстремуму немає.

23. Знайти мінімум функціонала J[y(х)] = dх.

Знайти екстремалі, перевірити умови Лежандра, Якобі, Вейєрштраса і визначити характер мінімуму.

В.у = sh(ах + b); через дві задані точки проходить одна і тільки одна екстремаль. Умови Лежандра і Якобі виконуються, а Вейєрштраса - ні. Слабкий min.

24. Знайти мінімум функціонала J[y(х)] =

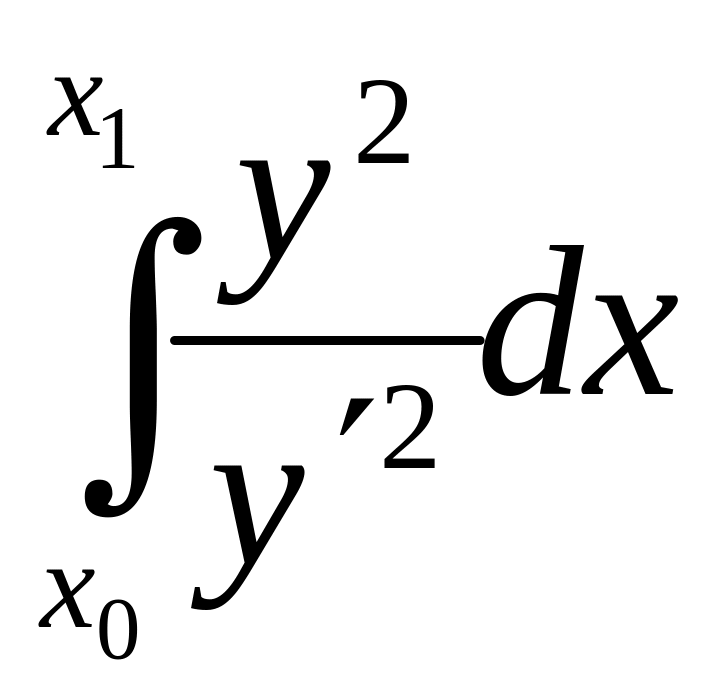
Знайти екстремалі, перевірити умови Лежандра, Якобі, Вейєрштраса і визначити характер мінімуму.

В.Екстремалі - параболи у = с(х + а)² , умови Лежандра і Якобі виконуються, а Вейєрштраса - ні. Слабкий min.

25 . Використовуючи достатні умови , дослідити на екстремум функціонали:

1. J[у(х)] = (у² - у'² )dх, y(0)=0 , y(T)=2

B. y=2sinx /sinT – max , 0 <T<π

2. J[у(х)] = x² у' ²dх, y(1)=3, y(2)=1.

B.y= -1 – mi n .

3. J[у(х)] = (2xу - у'² )dх, y(0)=1, y(6)=1

B.y=

4. J[у(х)] = у' ³dх, y(0)=0, y(3)=6.

B.y=2x – mi n .

5. J[у(х)] = у' ² ·y dх, y(0)=5, y(1)=5.

B.y=5 – слабкий mi n .

26. Дослідити на екстремум функціонали:

а) J[у(х)] = , y(0)=0, y(a)=b ,a, b>0.

б) J[у(х)] = , y(0)=0, y(a)=b ,a, b>0.

в) J[у(х)] = , y(1)=1, y(2)=4 .

г) J[у(х)] = , y(a)=A, y(b)=B .

В. а )слабкий min на прямій у=

б) слабкий min при у=

в) min при y=x².

г ) min на екстремалях y=sh(c₁ x+c₂) де c₁ i c₂ виражаються з рівнянь

A= sh(c₁ a+c₂), B= sh(c₁ b+c₂)

27. Дослідити на екстремум функціонали:

a) J[у] = (x² у'² +12y')dх, y(1)=1 , y(2)=8

б) J[у] = (у'² + у² +2уe^2x )dх, y(0)= , y(1)=

B. a) min при y=x²

б) min при y=

28. Перевірити , що : a) теорія екстремуму функціонала J[у(х)] = P(y(x)) |_x=a в просторі C _[a,b] співпадає із звичайною теорією екстремуму для функції F(ξ).

б) теорія екстремуму функціонала J[у(х)] =F(y(a),y(b)) в просторі C _[a,b] співпадає з теорією екстремуму для функції двох змінних F( ξ , ζ )