Міністерство освіти і науки України

Черкаський національний університет

ім.Б.Хмельницького

Григоренко В.К.

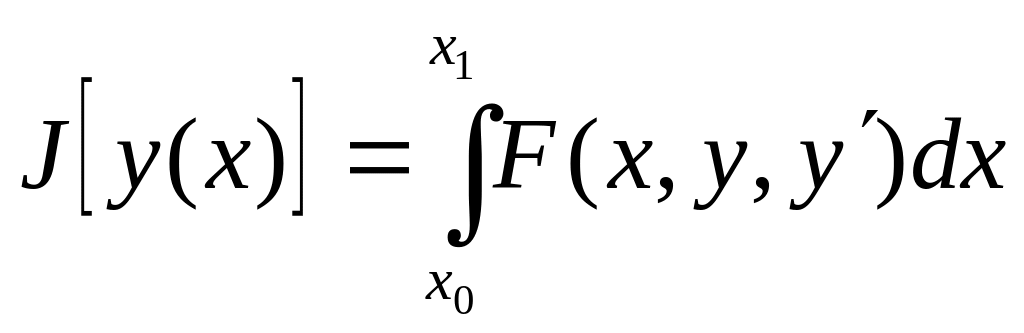
Черкаси 2001

Автор: Григоренко в.К.

Рекомендовано для самостійної роботи студентів, які вивчають варіаційне числення.

В посібнику вміщено короткі теоретичні відомості, зразки розв’язування типових задач, перелік завдань для аудиторної та домашньої роботи з відповідями і систему запитань до курсу з відповідями.

Схвалено до друку на засіданні кафедри математичного аналізу ЧДУ (протокол №4 від 28 грудня 2000р.)

§1. Екстремум функції багатьох змінних.

Нехай в деякій області D евклідового n- вимірного простору Е_n дана функція f(х₁,х₂,…,х_n) (коротко f(Х)).

Означення 1. В точці Х₀ D функція f(Х) має найбільше значення (найменше значення ), якщо для всіх Х D, маємо f(Х) f(Х₀) (f(Х) f(Х₀)).

Теорема Вейєрштрасса.

Будь – яка функція, неперервна на замкненій обмеженій області, приймає на ній своє найбільше і найменше значення.

Означення 2. Нехай функція f(Х) визначена в області D Е_n. Точка

Х₀=( ) D є точкою строго максимуму (строгого мінімуму) функції f(Х), якщо існує такий окіл точки Х₀, що виконується нерівність

f(Х) f(Х₀) (f(Х) f(Х₀)) )) для всіх точок X D, Х≠Х₀. Якщо ж для деяких X цього околу будуть виконуватись рівності: f(X) =f(Х₀), то точка Х₀ буде просто точкою максимуму або мінімуму.

Означення 3. Точки максимуму і мінімуму функції будуть точками екстремуму цієї функції.

Завдання для самостійної роботи.

1. Користуючись означенням, знайти точки екстремуму функції:

а) f(х₁,х₂)=

б) f(х₁,х₂)=

в) f(х₁,х₂)= в області D: .

Необхідна умова екстремуму.

Нехай функція f(X), X = (х₁,х₂,…,х _n) визначена в околі точки Х₀=( ).Якщо ця точка є точкою екстремуму функції f(X) і якщо в цій

точці існують похідні , то вони рівні нулю: .Така точка Х₀ називається стаціонарною. Якщо функція диференційована в точці Х₀, то її диференціал дорівнює нулю в цій точці.

Якщо включити і функції, які не є диференційованими в деяких точках, то необхідна умова видозміниться: якщо Х₀ є точкою екстремуму функції f(х₁, х₂,…,х_n), то в цій точці кожна з похідних або дорівнює нулю або не існує.

Приклад.

Функція z=x² - y² в точці (0,0) задовольняє необхідну умову екстремуму, але вона не є екстремальною точкою.

Достатні умови екстремуму.

Означення 4. Квадратична форма А(Х) = А(х₁,х₂,…,х_n) =

, називається додатньо (від'ємно) визначеною, якщо А(Х) > 0 (А(Х)< 0) для будь-якої точки X Е_n, X ≠ 0, а перетворюється в нуль тільки при X = 0, тобто при х₁ = 0, х₂ = 0, ...х_n= 0.

Квадратична форма, яка приймає і додатні і від'ємні значення називається невизначеною.

Теорема. (Достатня умова строгого екстремуму).

Нехай функція f(X) визначена і має неперервні похідні другого порядку включно в околі точки Х₀=( ) і Х₀ є стаціонарною точкою функції f(X). Якщо квадратична форма

(1) A(dx₁,dx₂,...,dx_n)=

(другий диференціал функції f в точці Х₀) є додатньо визначеною (від'ємно визначеною) квадратичною формою, то точка Х₀ є точкою строгого мінімуму (строгого максимуму); якщо квадратична форма (1) є невизначеною, то в точці Х₀ екстремуму немає.

Критерій Сільвестра додатної визначеності квадратичної форми.

Для того, щоб квадратична форма

(2) А(Х) = А(х,. х₂ x_n) =

в якій , була додатньо визначеною, необхідно і достатньо, щоб

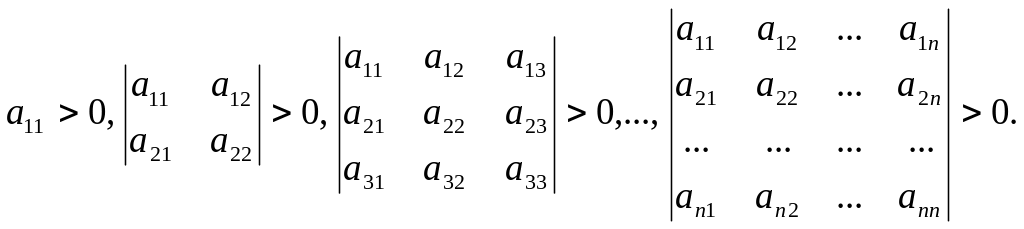
Для того, щоб квадратична форма була від’ємно визначеною, необхідно і достатньо, щоб

Випадок n=2. нехай функція f(х,у) визначена і має неперервні частинні похідні другого порядку в деякому околі точки (х₀,у₀) і точка (х₀,у₀) є стаціонарною точкою, тобто f^’_х(х₀,у₀)= f^’_у(х₀,у₀) (3).

Тоді, якщо в точці (х₀,у₀): = , (4) то вона є точкою екстремуму функції, і якраз є точкою максимуму, якщо в ній і мінімуму, якщо .

Якщо ж в жодній точці(х₀,у₀): = , то екстремуму в точці (х₀,у₀) немає.

Якщо ж в точці (х₀,у₀): = , то необхідне додаткове дослідження для з’ясування чи буде в цій точці екстремум.

Задача 1. Розгляньте функції

а) ;

б) ;

в) .

Точка (0,0) є стаціонарною для кожної з цих функцій і для кожної з функцій . Чи буде екстремум в цій точці для кожної із функцій?

Приклад. Знайти екстремум функції трьох змінних:

Розв’язання.

Знаходимо стаціонарні точки функції f. Для цього складемо систему рівнянь

Розв’язки її х₀=-2/3; у₀=-1/3; z₀=1. складаємо квадратичну форму (1) в точці Р(-2/3,-1/3,1). Маємо:

; ; ;

; ; ;

; ; ;

В точці, в Р маємо:

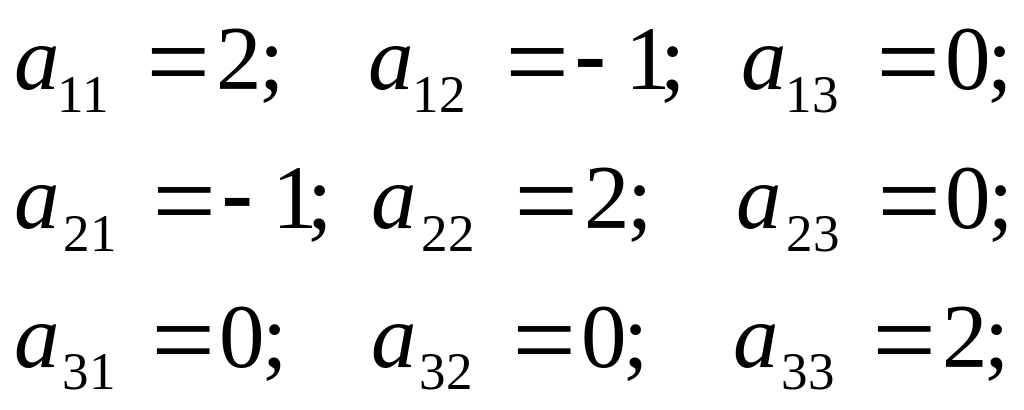
Маємо далі

;

Використовуючи критерій Сильвестра, отримуємо, що квадратична форма – додатньо визначена, бо в точці Р функція має мінімум, причому

f (Р)=-4/3.

Завдання для самостійної роботи.

Дослідити на екстремум функції:

1)

2)

3)

4)

5)

6)

7)

8) , (при -

при - немає екстремуму).