Задача д.6

Умова задачі. Однорідна горизонтальна платформа (кругла радіуса R або прямокутна зі сторонами R і 2R, де R=1,5 м) маси m₁=30 кг обертається з кутовою швидкістю ω₀=10 с^-1 навколо вертикальної осі z, яка відстоїть від центра мас C на відстані OC=b (рис. Д.6.0.—Д.6.9, таблиця 16. Умови задач Д.6.0.—Д.6.9, таблиця 17. Умови задач Д.6.0.А—Д.6.9.А, таблиця 18. Умови задач Д.6.0.Б—Д.6.9.Б). Розміри для всіх прямокутних платформ показані на рис. Д.6.0,а (вид зверху).

В момент часу t₀ =0 по жолобу платформи починає рухатись (під дією внутрішніх сил) тягар D маси m₂=10 кг за законом S=AD=f(t), де S виражено в метрах, t—в секундах. Одночасно на платформи, які зображені на рис. Д.6.0—Д.6.4 починає діяти пара сил з моментом M, який задано в Ньютон-метрах. При M<0 його напрям протилежний показаному на рисунках. Для платформ, які показані на рис. Д.6.5—Д.6.9, M=0.

Визначити: для платформ, які зображені на рис. Д.6.0 -Д.6.4, залежність , тобто кутову швидкість платформи, як функцію часу; для платформ, які зображені на рис. Д.6.5—Д.6.9, кутову швидкість ω₁ платформи в момент часу t₁=1 c.

Форма жолоба на рис. Д.6.0—Д.6.4 прямолінійна (жолоб KE), на рис. Д.6.5—Д.6.7—коло радіуса R (обід платформи), а на рис. Д.6.8 - Д.6.9 – коло радіуса r=0,5R. На всіх рисунках тягар D показаний в положенні, при якому S>0. Коли S<0, тягар D знаходиться з протилежного боку від точки А. На рис. Д.6.5—Д.6.9 відстань відлічується по дузі кола. При розв’язанні задачі краще робити вигляд платформи зверху і провести вісь z на заданій відстані OC=b від центра C. Якщо OC=b=0, то вісь z проходить через точку С—центр платформи.

Методичні вказівки. Задача Д.6—на застосування теореми про зміну кінетичного моменту системи відносно осі z:

,

де K_z—кінетичний момент системи відносно осі обертання z. Величина K_z визначається як сума кінетичних моментів платформи і тягаря. При цьому необхідно врахувати, що абсолютна швидкість тягаря складається геометрично з відносної швидкості і переносної швидкості :

.

А тому і кількість руху тягаря визначається за формулою

.

Скориставшись теоремою Варіньона, можна записати для кінетичного моменту тягаря

.

Сума моментів зовнішніх сил в даній задачі дорівнює тільки моменту пари сил M для рис. Д.6.0—Д.6.4, тому для них

.

В цих варіантах в останньому рівнянні необхідно розділити змінні і проінтегрувати, враховуючи, що

,

де у загальному випадку для прямокутної платформи момент інерції відносно осі обертання визначається за теоремою Штейнера—Гюйгенса так:

;

,

а для круглої платформи

;

.

Кінетичний момент тягаря:

,

де , .

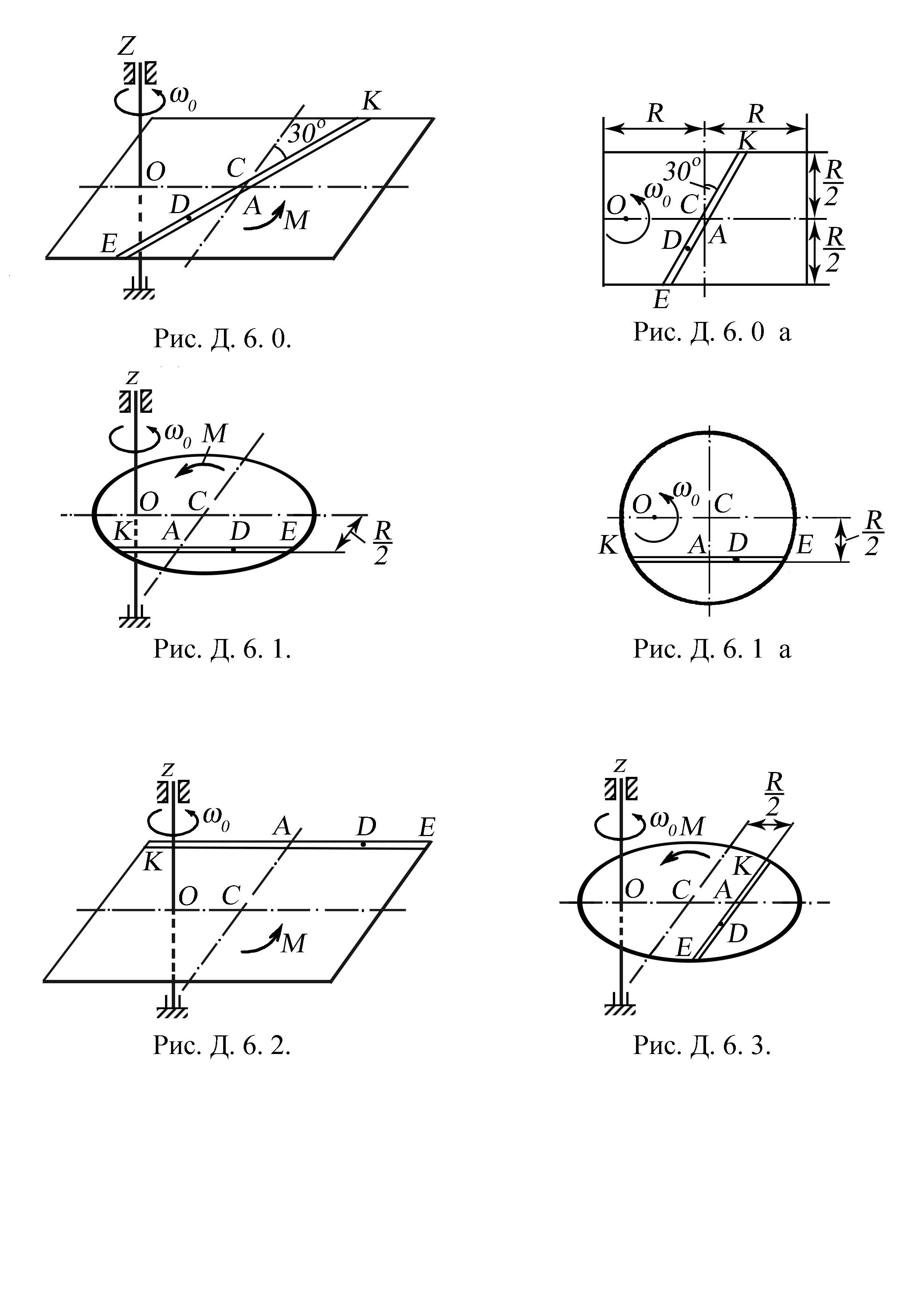
Рисунки до задач Д. 6. 0. – Д. 6. 3.

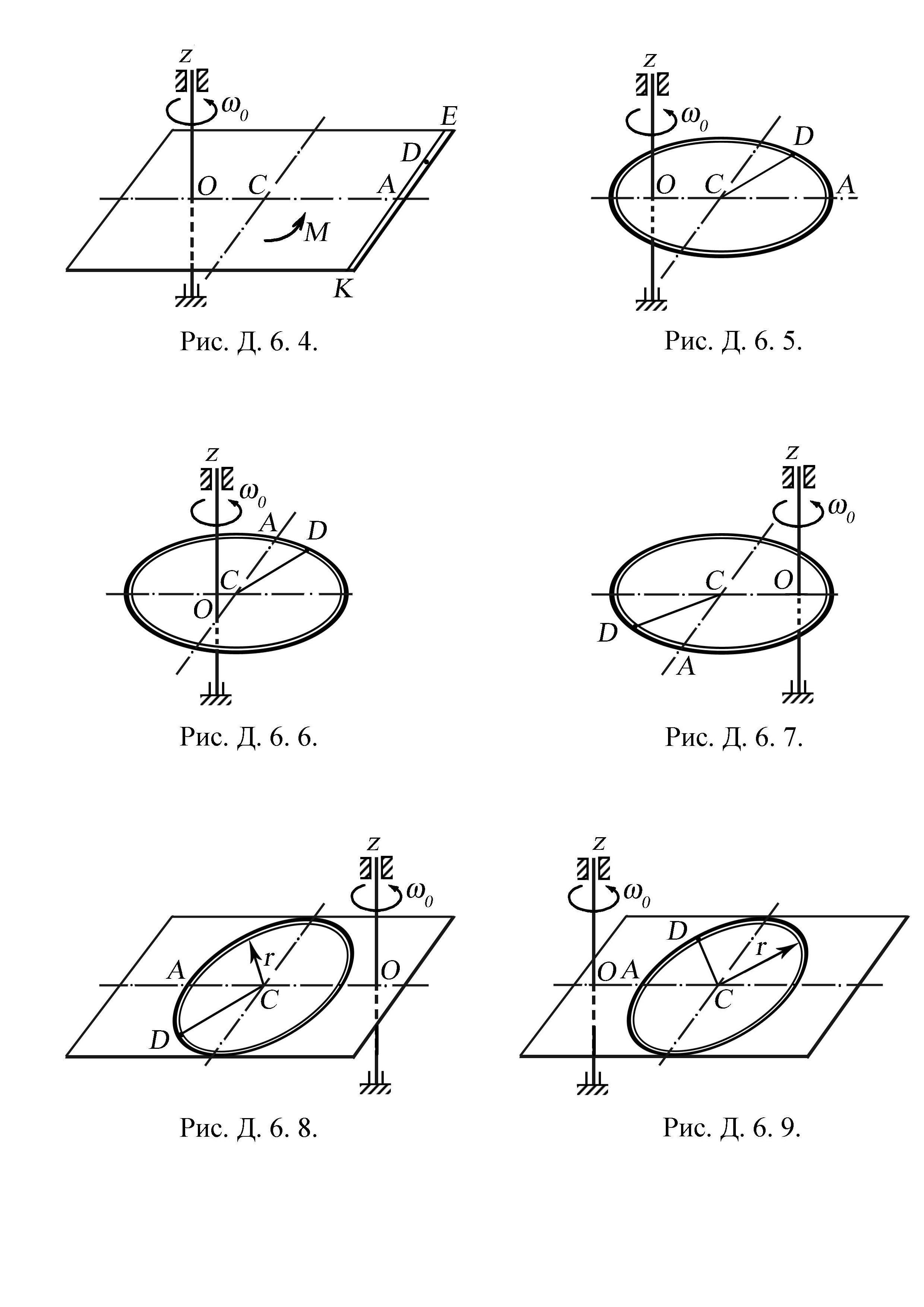
Рисунки до задач Д. 6. 4 – Д. 6. 9.

У випадку, коли М=0 (рис. Д.6.5—Д.6.9) і необхідно обчислити ω₁, потрібно скористатись законом збереження кінетичного моменту

,

де - кінетичний момент системи при t₀=0, - кінетичний момент системи в момент часу t₁. При цьому спочатку необхідно знайти і показати на рисунку положення D₀ і D₁ тягаря в моменти часу t₀=0 і t₁ відповідно.

За правильне розв’язання задачі Д.6 з використанням даних таблиці 16. Умови задач Д.6.0—Д.6.9 студент одержує оцінку “задовільно”. За правильне розв’язання задачі Д.6 з використанням даних таблиці 17. Умови задач Д.6.0.А—Д.6.9.А студент одержує оцінку “добре”, а з використанням таблиці 18. Умови задач Д.6.0.Б—Д.6.9.Б—оцінку “відмінно”.