2.4.3 Принципы оптимального поведения и принятия решения в условиях неопределенности

Для выработки оптимального поведения ЛПР такую ситуацию полезно моделировать, как антагонистическую игру двух лиц, где в качестве противника ЛПР рассматривается природа. Последняя наделяется всеми мыслимыми в данных условиях возможностями.

В «играх с природой» существуют свои специфические (хотя и напоминающие принцип минимакса) принципы оптимального выбора решения.

Принцип крайнего пессимизма (критерий Вальда) Согласно этому принципу игра с природой (принятие решения в условиях неопределенности) ведется как с разумным, агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оптимальной считается стратегия ЛПР, при которой гарантируется выигрыш не меньший, чем «разрешенный природой».

Принцип минимаксного риска (критерий Сэвиджа).Этот принцип также пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на «выигрыш», а на риск. Риск определяется как разность между максимальным выигрышем ЛПР (при условии полной информации о состоянии природы) и реальным выигрышем (при незнании состояния природы). В качестве оптимальной выбирается та стратегия, при которой величина риска минимальна.

Принцип пессимизма-оптимизма (критерий Гурвица). Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом («всегда рассчитывай на худшее!»), ни крайним оптимизмом («авось, кривая вывезет!»). Согласно этому критерию максимизируется взвешенное среднее между выигрышами крайнего пессимизма и крайнего оптимизма. Причем «вес» выбирается из субъективных соображений об опасности ситуации.

2.5 Примеры составления математических моделей Пример 2.5.1

Пусть некоторый экономический регион производит несколько (n) видов продуктов исключительно своими силами и только для населения данного региона. Предполагается, что технологический процесс отработан, а спрос населения на эти товары изучен. Надо определить годовой объем выпуска продуктов, с учетом того, что этот объем должен обеспечить как конечное, так и производственное потребление.

Составим математическую модель этой задачи.

По ее условию даны: виды продуктов, спрос на них и технологический процесс; требуется найти объем выпуска каждого вида продукта Обозначим известные величины: c _i — спрос населения на i-й продукт (i=1,...,n); a _ij — количество i-го продукта, необходимое для выпуска единицы j -го продукта по данной технологии ( i=1,...,n ; j=1,...,n);

Обозначим неизвестные величины:

х_i – объем выпуска i-го продукта (i=1,...,n);

Совокупность с = ( c₁ ,...,c_n ) называется вектором спроса, числа a_ij – технологическими коэффициентами, а совокупность х =( х₁ ,...,х_n ) – вектором выпуска.

По условию задачи вектор х распределяется на две части: на конечное потребление (вектор с ) и на воспроизводство (вектор х-с ). Вычислим ту часть вектора х которая идет на воспроизводство. По нашим обозначениям для производства х_j количества j-го товара идет a_ij · х_j количества i-го товара. Тогда сумма a_i1 · х₁ +...+ a_in · х_n показывает ту величину i-го товара, которая нужна для всего выпуска х =( х₁ ,...,х_n ). Следовательно, должно выполняться равенство:

х_i - с_i = a_i1 · х₁ +...+ a_in · х_n

Распространяя это рассуждение на все виды продуктов, приходим к искомой модели:

х₁ - с₁ = a₁₁ · х₁ +...+ a_1n · х_n х₂ - с₂ = a₂₁ · х₂ +...+ a_2n · х_n .................................................... х_n - с_n = a_n1 · х_n +...+ a_nn · х_n

Решая эту систему из n линейных уравнений относительно х₁ ,...,х_n и найдем требуемый вектор выпуска.

Для того, чтобы написать эту модель в более компактной (векторной) форме, введем обозначения:

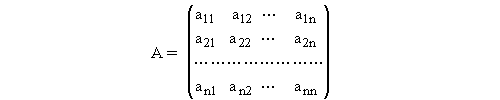
Квадратная (n^xn) – матрица А называется технологической матрицей. Легко проверить, что наша модель теперь запишется так: х-с =Ах или

Получили классическую модель «Затраты-выпуск», автором которой является известный американский экономист В. Леонтьев.