2.7 Оформлення літературних посилань

При написанні розрахункової роботи студент повинен обов’язково давати посилання на інформаційні джерела, матеріали з яких (формули, таблиці, схеми, графіки, висновки тощо) наводяться в розрахунковій роботі. Посилатися слід на останні видання публікацій. На більш ранні видання можна посилатися лише в тому разі, коли в них є матеріал, який не включено до останнього видання. Якщо студент використовує відомості, матеріали з монографій, оглядових статей, інших джерел з великою кількістю сторінок, тоді в посиланні необхідно точно вказати номери сторінок, що містять використані студентом цитати, ілюст­рації, таблиці, формули.

Посилання розміщується в квадратних дужках і містить порядковий номер джерела в списку використаних інформаційних джерел (додаток Б) із зазначенням сторінок, на яких знаходиться використаний матеріал, наприклад: [1, с.7]. Посилання може також розміщуватися під текстом сторінки з цитатою у вигляді виноски, в якій вказують прізвище та ініціали автора, назву джерела, видавництво, рік видання та сторінку.

При посиланні на рисунки чи таблиці вказують порядковий номер ілюстрації, наприклад, “рис.2.1”. При повторному посиланні вказують “див. рис.2.2”. При посиланнях на формули вказують порядковий номер формули в круглих дужках, наприклад: “у формулі (1.2)”.

Додаток

Державний вищий навчальний заклад

«Українська академія банківської справи

Національного банку України»

Кафедра економічної кібернетики

ПОЯСНЮВАЛЬНА ЗАПИСКА ДО РОЗРАХУНКОВОЇ РОБОТИ

з дисципліни “ Економіко-математичні методи і моделі

(оптимізаційні методи і моделі) ”

Виконав студент 2 курсу групи ЕК- _________________

2011.12.02

Керівник канд. екон. наук, доцент _______________ О.В.Кузьменко

2011.12.02

Побудова та зміст документа відповідає

вимогам ДСТУ 30008-95 ________________ О.В.Кузьменко

2011.12.02

Суми - 2011

ЗМІСТ

ВСТУП ………………………………………………………………………………….. 3

ЗАДАЧА 1 ………………………………………………………………………………. 4

ЗАДАЧА 2 ………………………………………………………………………………. 8

ЗАДАЧА 3 ………………………………………………………………………………. 14

ЗАДАЧА 4 ………………………………………………………………………………. 20

ЗАДАЧА 5 ………………………………………………………………………………. 26

СПИСОК ЛІТЕРАТУРИ ……………………………………………………………….. 29

ВСТУП

Економіко-математичне моделювання є галуззю економічної науки, яка вивчає основні принципи та інструментарій постановки економічних задач, побудови їх математичних моделей, методів розв’язування та аналізу економічних задач з метою використання отриманих результатів в економіці. Метою розрахункової роботи є вивчення методів розв’язування різних типів економічних задач.

В розрахунковій роботі розглядаються основні методи розв’язування, аналізу та використання задач зі знаходженням екстремуму функції на множині допустимих варіантів у широкому спектрі теоретико-економічних та практичних проблем.

ЗАДАЧА 1

Побудувати на площині множину розв’язків (багатокутник) системи лінійних обмежень-нерівностей й геометрично знайти найбільше та найменше значення лінійної функції в цьому багатокутнику (x₁0, x₂0).

Розв’язання

Задана економіко-математична модель є моделлю задачі лінійного програмування, що містить лише дві змінні, і тому може бути розв’язана графічно.

Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто у визначенні такої області, де водночас виконуються всі обмеження моделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис.1.1.).

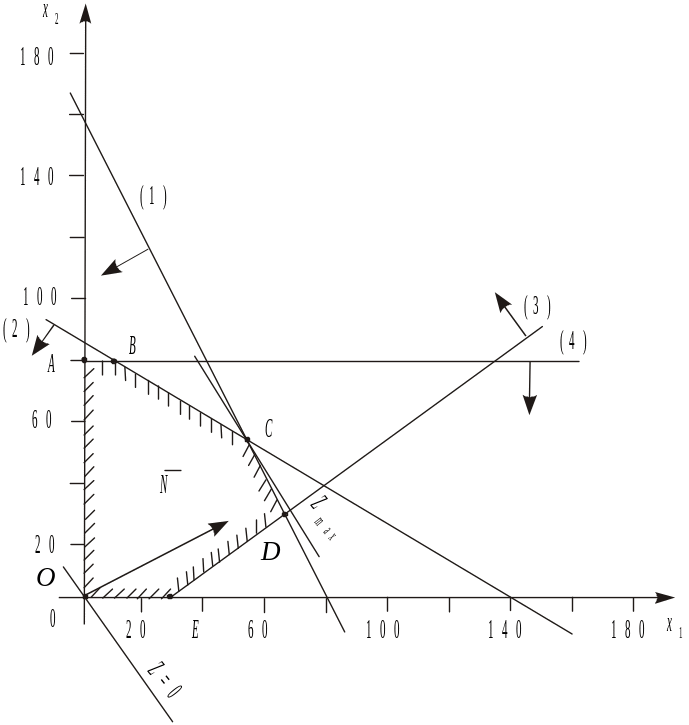
Рисунок 1.1

Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину (на рис.1.1 її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. Інакше таким зображенням є інша півплощина.

Умова невід’ємності змінних х₁ ≥ 0, х₂ ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі — шестикутник OABCDE. Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід’єм­ності змінних. Тому поставлену задачу буде розв’язано, якщо ми зможемо відшукати таку точку багатокутника OABCDE, в якій цільова функція Z набирає найбільшого та найменшого значення.

Для цього побудуємо вектор , координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор завжди виходить із початку координат і напрямлений до точки з координатами (х₁ = с₁; х₂ = с₂). У нашій задачі вектор . Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.

Побудуємо лінію, що відповідає, наприклад, значенню Z=0. Це буде пряма 50х₁ + 30х₂ = 0, яка перпендикулярна до вектора і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 50х₁ + 30х₂ = 0 паралельно самій собі згідно з напрямом вектора доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.

Із рис.1.1 видно, що останньою спільною точкою прямої цільової функції та багатокутника OABCDE є точка С. Координати цієї точки є оптимальним планом задачі.

Координати точки С є розв’язком системи рівнянь

(1.1)

(1.2)

звідси маємо: х₁ = 50; х₂ = 60.

Отже,

Виходячи з аналогічних міркувань, знаходимо, що , х₁ = 0; х₂ = 0.

Перевіримо правильність рішення задачі за допомогою MS Excel (див.рис.1.2-1.6).

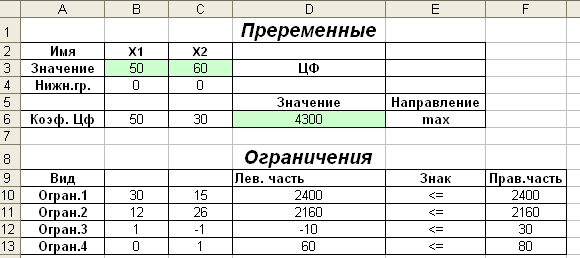
Рисунок 1.2

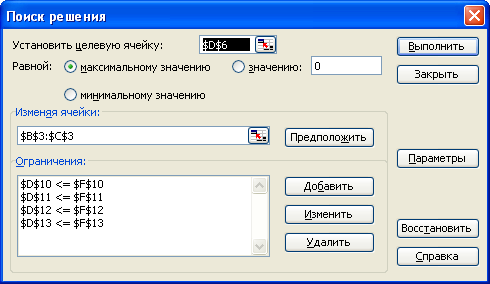
Рисунок 1.3

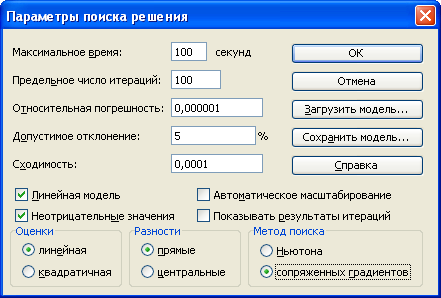
Рисунок 1.4

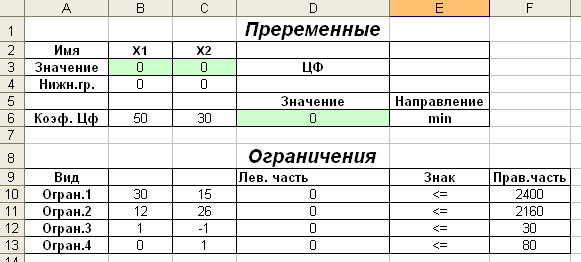
Рисунок 1.5

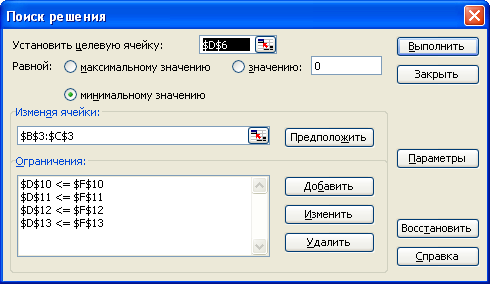
Рисунок 1.6

ЗАДАЧА 2

Симплексним методом знайти розв’язок задачі.

Розв’язання

2.1 Знаходження першого опорного плану задачі

Запишемо систему обмежень задачі в канонічному вигляді. Для цього перейдемо від обмежень-нерівностей до строгих рівнянь, увівши до лівої частини обмежень додаткові змінні х₅ та х₆:

(2.1)

У цільовій функції Z додаткові змінні мають коефіцієнти, які дорівнюють нулю:

(2.2)

Канонічну систему обмежень задачі запишемо у векторній формі:

(2.3)

де

(2.4)

Оскільки вектори та одиничні та лінійно незалежні, то саме з них складається початковий базис у зазначеній системі век­торів. Змінні задачі х₅ та х₆, що відповідають одиничним базисним векторам, називають базисними, а решту — вільними змінними задачі лінійного програмування. Прирівнюючи вільні змінні до нуля, з кожного обмеження задачі дістаємо значення базисних змінних:

(2.5)

Згідно з визначеними векторна форма запису системи обмежень цієї задачі матиме вигляд:

. (2.6)

Оскільки додатні коефіцієнти х₅ та х₆ відповідають лінійно незалежним векторам, то за означенням

(2.7)

є опорним планом задачі і для цього початкового плану

. (2.8)

2.2 Складання симплексної таблиці для першого опорного плану

Складемо симплексну таблицю для першого опорного плану задачі.

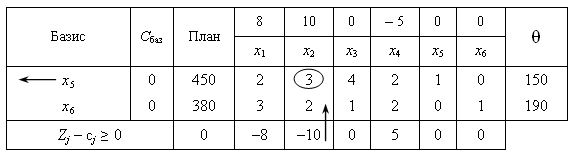
Елементи останнього рядка симплекс-таблиці є оцінками _j, за допомогою яких опорний план перевіряють на оптимальність. Їх визначають так:

; (2.9)

; (2.10)

; (2.11)

; (2.12)

; (2.13)

. (2.14)

У стовпчику «План» оцінкового рядка записуємо значення цільової функції Z, якого вона набуває для визначеного опорного плану: .

2.3 Перевірка опорного плану на оптимальність

Після обчислення всіх оцінок опорний план перевіряємо на оптимальність. Для цього продивляємось елементи оцінкового рядка. Якщо всі (для задачі на max) або (для задачі на min), то визначений опорний план є оптимальним. Якщо ж в оцінковому рядку є хоча б одна оцінка, що не задовольняє умову оптимальності (від’ємна в задачі на max або додатна в задачі на min), то опорний план є неоптимальним і його можна поліпшити.

У цій задачі в оцінковому рядку дві оцінки та від’ємні, тобто не задовольняють умову оптимальності, і тому перший визначений опорний план є неоптимальним. За алгоритмом симплекс-методу необхідно від нього перейти до іншого опорного плану задачі.

2.4 Перехід від одного опорного плану до іншого

Перехід від одного опорного плану до іншого здійснюють зміною базису, тобто через виключення з поточного базису якоїсь змінної та включення замість неї нової з числа вільних змінних.

Для введення до нового базису вибираємо змінну х₂, оскільки їй відповідає найбільша за абсолютною величиною оцінка з-поміж тих, які не задовольняють умову оптимальності (|–10|>|–8|).

Щоб визначити змінну, яка підлягає виключенню з поточного базису, для всіх додатних елементів стовпчика «х₂» знаходимо відношення і вибираємо найменше значення. Згідно з даними симплексної таблиці маємо, що , і тому з базису виключаємо змінну х₅, а число а₁₂ = 3 — розв’язувальний елемент. Дальший перехід до нового опор­ного плану задачі полягає в побудові наступної симплексної таблиці, елементи якої розраховуємо за методом Жордана–Гаусса.

Друга симплексна таблиця має такий вигляд:

У цій таблиці спочатку заповнюємо два перших стовпчики «Базис» і «С_баз», а решту елементів нової таблиці розраховуємо за розглянутими нижче правилами:

1. Кожний елемент розв’язувального (напрямного) рядка необхідно поділити на розв’язувальний елемент і отримані числа записати у відповідний рядок нової симплексної таблиці.

2. Розв’язувальний стовпчик у новій таблиці записують як одиничний з одиницею замість розв’язувального елемента.

3. Якщо в напрямному рядку є нульовий елемент, то від­повідний стовпчик переписують у нову симплексну таблицю без змін.

4. Якщо в напрямному стовпчику є нульовий елемент, то відповідний рядок переписують у нову таблицю без змін.

Усі інші елементи наступної симплексної таблиці розраховують за правилом прямокутника.

Щоб визначити будь-який елемент нової таблиці за цим правилом, необхідно в попередній симплексній таблиці скласти умовний прямокутник, вершини якого утворюються такими числами:

1 – розв’язувальний елемент (число 1);

2 – число, що стоїть на місці елемента нової симплексної таблиці, який ми маємо розрахувати;

3 та 4 – елементи, що розміщуються в двох інших протилежних вершинах умовного прямокутника.

Необхідний елемент нової симплекс-таблиці визначаємо за такою формулою:

.

Наприклад, визначимо елемент , який розміщується в новій таблиці в другому рядку стовпчика «х₄». Складемо умовний прямокутник:

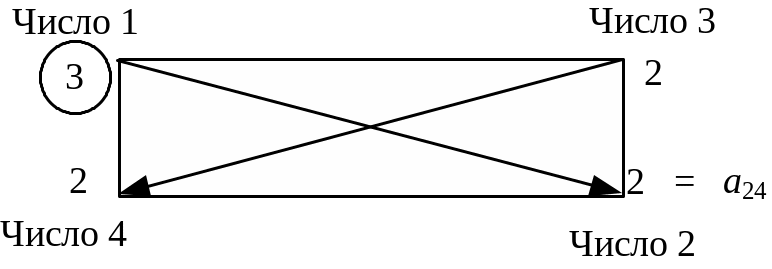
Тоді . Це значення записуємо в стовпчик «х₄» у другому рядку другої симплексної таблиці.

Аналогічно розраховуємо усі елементи нової симплексної таблиці, у тому числі й елементи стовпчика «План» та оцінкового рядка. Наявність двох способів зображення визначення оцінок опорного плану (за правилом прямокутника та за відповідною формулою) дає змогу контролювати правильність арифметичних обчислень на кожному кроці симплекс-методу.

Після заповнення нового оцінкового рядка перевіряємо виконання умови оптимальності Z_j – с_j ≥ 0 для другого опорного плану. Цей план також неоптимальний, оскільки . Використовуючи процедуру симплекс-методу, визначаємо третій опорний план задачі, який наведено у вигляді таблиці:

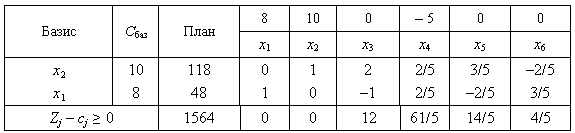
В оцінковому рядку третьої симплексної таблиці немає від’ємних чисел, тобто всі і задовольняють умову оптимальності. Це означає, що знайдено оптимальний план задачі:

(2.15)

або

Х* = (48; 118; 0; 0; 0; 0); (2.16)

. (2.17)

Перевіримо правильність рішення задачі за допомогою MS Excel (див.рис.2.1-2.3).

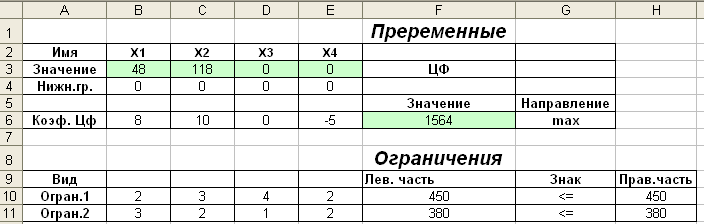
Рисунок 2.1

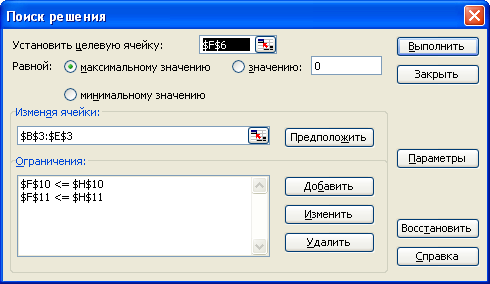
Рисунок 2.2

Рисунок 2.3

ЗАДАЧА 3

Побудувати двоїсту задачу до заданої та знайти її розв’язок. Використовуючи теореми двоїстості знайти розв’язок прямої задачі. Задана пряма задача має вигляд:

max Z = – 5x₁ + 2x₂;

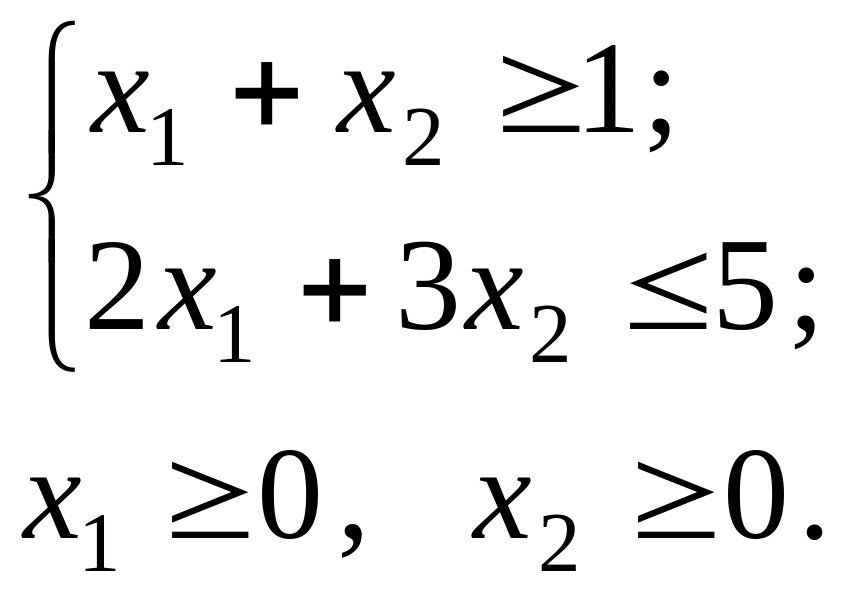
Розв’язання

Двоїста задача утворюється за такими правилами:

1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.

2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень двоїстої задачі дорівнює кількості невідомих прямої задачі.

3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі – на визначення найменшого значення (min), і навпаки.

4. Коефіцієнтами при змінних у цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.

Двоїстою до задачі

max Z=c₀ + (c, x),

Ax=b, x0,

(записаній у векторно-матричній формі) є

,

, y0,

де – матриця, транспонована до А; (с, x), (b, y) – скалярні добутки відповідних векторів.

Перш ніж записати двоїсту задачу, необхідно пряму задачу звести до стандартного вигляду. Оскільки цільова функція Z максимізується і в системі обмежень є нерівності, то їх слід звести до виду « ». Тому перше обмеження задачі помножимо на (–1). Після цього знак нерівності зміниться на протилежний. Отримаємо:

max Z = – 5x1 + 2x2; (3.1)

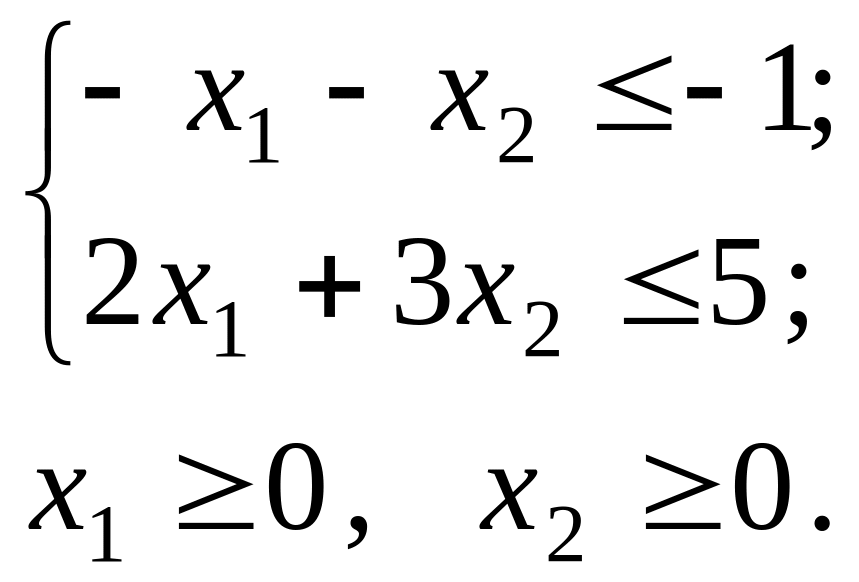(3.2)

За наведеними вище правилами складемо двоїсту задачу:

min F = – y1 + 5y2; (3.3)

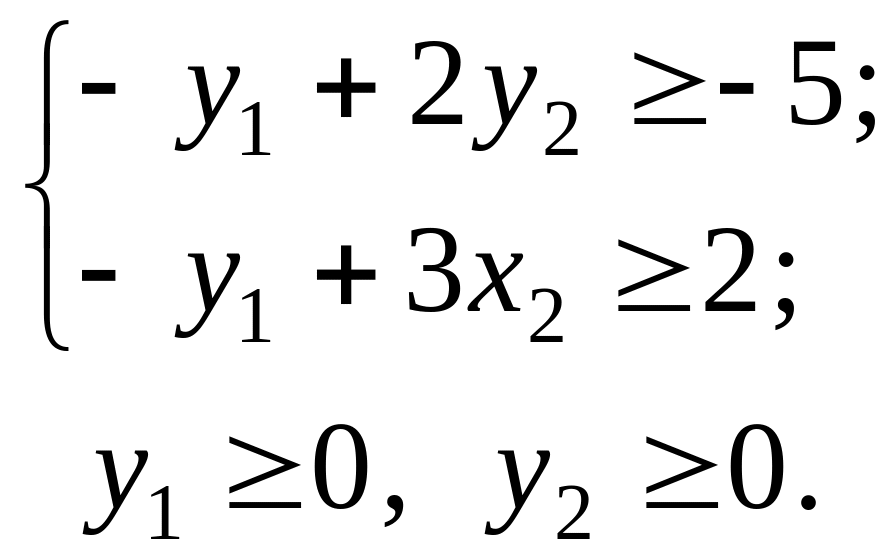(3.4)

Оскільки записані задачі симетричні (обмеження прямої та двоїстої задач є лише нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень), то будь-яку з них можна розв’язати симплекс-методом. Наприклад, визначимо спочатку оптимальний план прямої задачі. Для цього застосуємо алгоритм симплекс-методу.

1. max Z = – 5x₁ + 2x₂ + 0x₃ + 0x₄; (3.5)

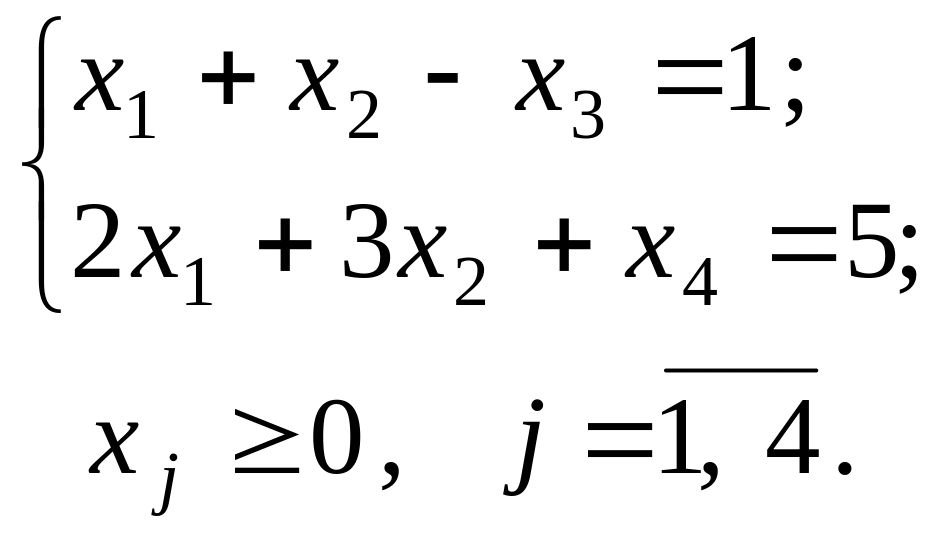(3.6)

2. Векторна форма запису системи обмежень має вигляд:

, (3.7)

де , , , , .

У системі векторів для утворення початкового одиничного базису відсутній один вектор. Тому введемо штучну змінну в перше обмеження.

3. Розширена задача лінійного програмування буде такою:

max Z = – 5x₁ + 2x₂ + 0x₃ + 0x₄ – Мx₅; (3.8)

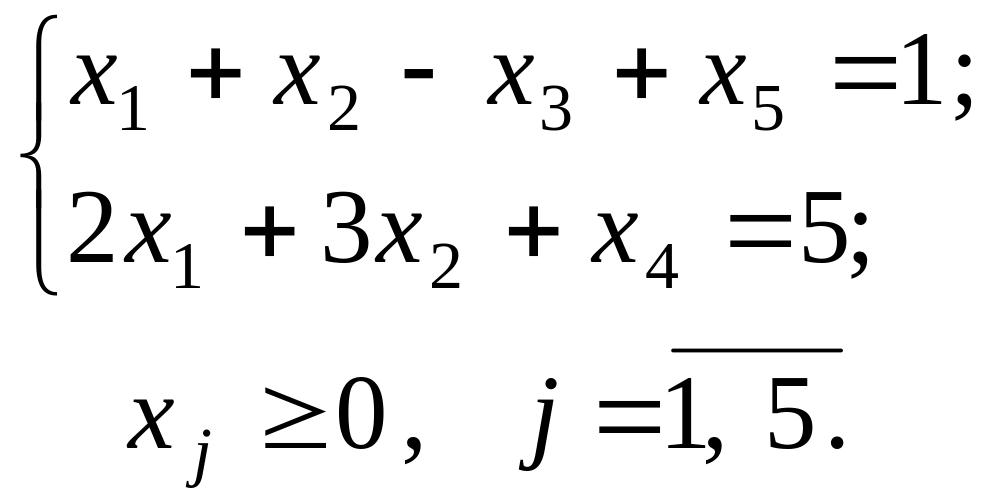(3.9)

У цій задачі х₄ та х₅ – базисні змінні, а х₁, х₂, х₃ – вільні. Нехай х₁=х₂=х₃=0, тоді х₄=5; х₅=1.

Перший опорний план задачі:

X₀=(0; 0; 0; 5; 1), Z₀ = – M. (3.10)

4. Подальше розв’язування прямої задачі подано у вигляді симплексної таблиці:

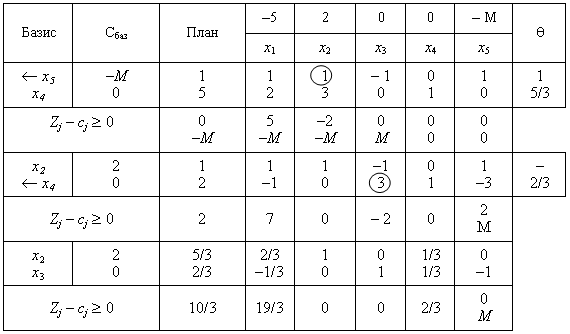
З останньої симплекс-таблиці запишемо оптимальний план прямої задачі:

Х*=(0; 5/3; 2/3; 0), Zmax = 10/3. (3.11)

Згідно зі співвідношенням двоїстості за першою теоремою (якщо одна з пари спряжених задач має оптимальний план, то й друга задача також має розв’язок, причому для оптимальних розв’язків значення цільових функцій обох задач збігаються) можна зробити висновок, що оптимальний план двоїстої задачі існує і

min F = max Z = 10/3. (3.12)

Компоненти вектора Y^* (оптимальний план двоїстої задачі) визначимо за формулою:

, (3.13)

де та міститься в стовпчику «с_баз» останньої симплекс-таблиці;

. (3.14)

Матриця D^{– 1} також міститься в останній симплекс-таблиці у стовпчиках змінних «x₅» та «x₄», які утворювали початковий базис.

Отже,

, (3.15)

min F = – 10 + 52/3 = 10/3. (3.16)

Застосувавши для розв’язування прямої задачі симплекс-метод, ми знайшли її оптимальний план, а потім визначили оптимальний розв’язок двоїстої задачі за допомогою співвідношень першої теореми двоїстості.

Перевіримо правильність рішення прямої задачі за допомогою MS Excel (див.рис.3.1-3.3).

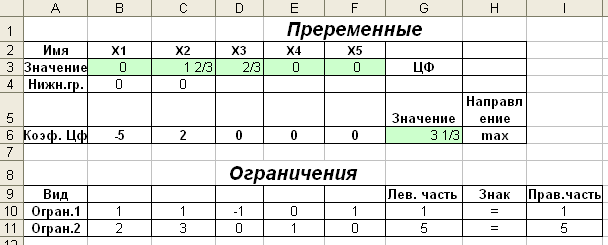
Рисунок 3.1

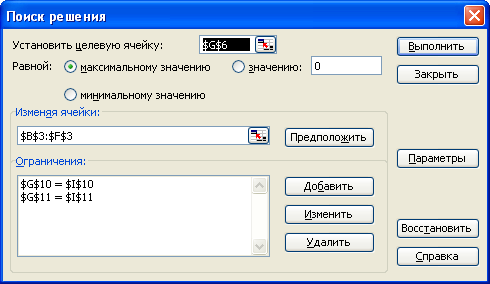
Рисунок 3.2

Рисунок 3.3

Перевіримо правильність рішення двоїстої задачі за допомогою MS Excel (див.рис.3.4-3.6).

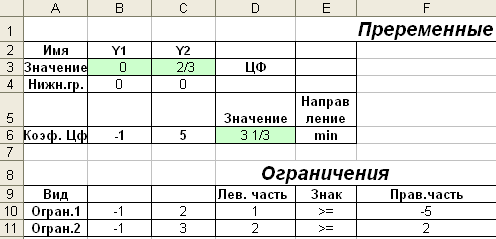
Рисунок 3.4

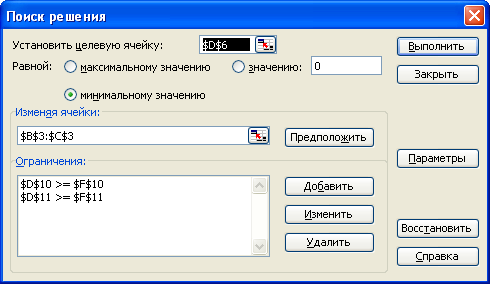
Рисунок 3.5

Рисунок 3.6

ЗАДАЧА 4

Компанія контролює три фабрики А₁, А₂, А₃, здатні виготовляти відповідно 150, 60 та 80 тис.од.продукції щотижня. Вона уклала договір із чотирма замовниками В₁, В₂, В₃, В₄, яким потрібно щотижня доставляти відповідно 110, 40, 60 та 80 тис.од.продукції. Вартість транспортування 1 тис.од.продукції замовникам з кожної фабрики наведена в таблиці:

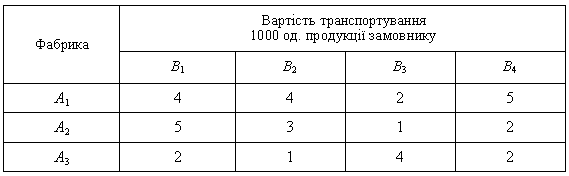
Необхідно визначити оптимальний план перевезень продукції від кожної фабрики до замовників, що мінімізує загальну вартість транспортних послуг.

Розв’язання

4.1 Побудова математичної моделі

Нехай x_ij – кількість продукції, що перевозиться з і-ої фабрики до j-го замовника . Загальні витрати, пов’язані з транспортуванням продукції, визначаються як сума добутків обсягів перевезеної продукції на вартості транспортування 1 тис.од. продукції до відповідного замовника і за умовою задачі мають бути мінімальними. Оскільки транспортна задача за умовою є збалансованою, закритою 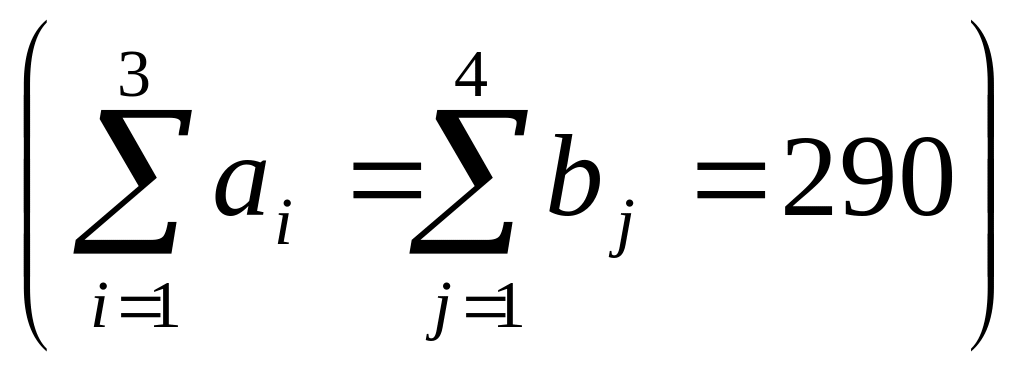, то математична модель сформульованої задачі має вигляд:

min Z = 4x₁₁ + 4x₁₂ + 2x₁₃ + 5x₁₄ + 5x₂₁ + 3x₂₂ + x₂₃ + 2x₂₄ + 2x₃₁ + x₃₂ ++ 4x₃₃ +2x₃₄

за умов:

4.2 Знаходження першого опорного плану задачі

Запишемо умови задачі у вигляді транспортної таблиці (табл.4.1) та складемо її перший опорний план у цій таблиці методом мінімальної вартості.

Таблиця 4.1

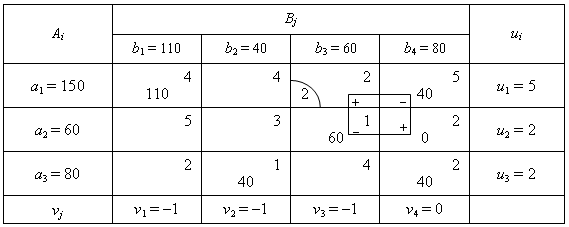
Загальна вартість перевезень продукції згідно з першим опорним планом визначається у такий спосіб:

Z₁ = 4110 + 540 + 160 + 140 + 240 = 820 (ум. од.). (4.3)

Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п’яти, а (m+n–1) = 3+4–1=6.

Для дальшого розв’язування задачі необхідно в одну з порожніх клітинок записати «нульове перевезення» так, щоб не порушити опорності плану, тобто можна зайняти будь-яку пусту клітинку, яка не утворює замкненого циклу із заповненими клітинами. Наприклад, заповнимо нулем клітинку А₂В₄. Тепер перший план транспортної задачі є невиродженим, і його можна перевірити на оптимальність методом потенціалів.

4.3 Перевірка опорного плану на оптимальність

На основі першої умови оптимальності u_i + v_j = c_ij складемо систему рівнянь (для заповнених клітин таблиці) для визначення потенціалів першого опорного плану:

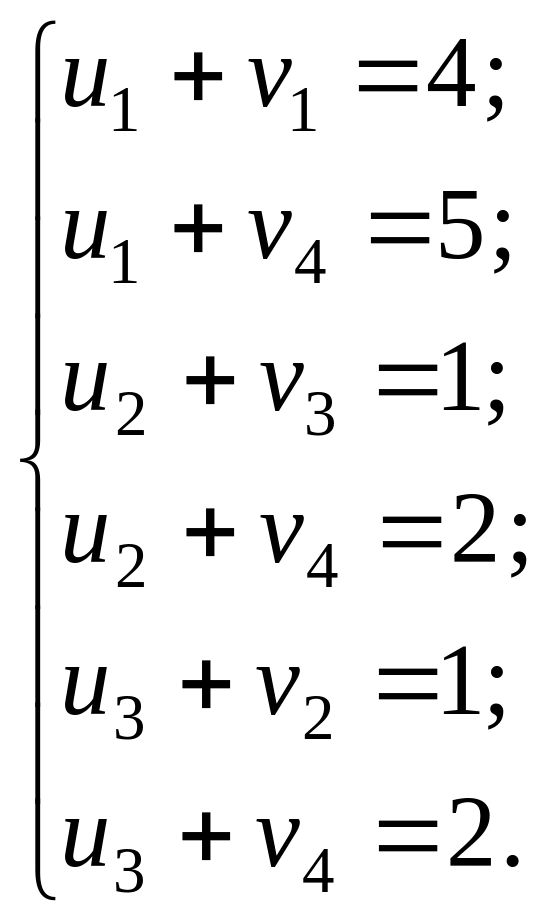(4.4)

Записана система рівнянь є невизначеною, і один з її розв’язків дістанемо, узявши, наприклад, v₄ = 0. Тоді всі інші потенціали однозначно визначаються з цієї системи рівнянь: u₁=5, u₂=2, u₃=2, v₁= – 1, v₂= – 1, v₃= – 1. Ці значення потенціалів першого опорного плану записуємо у транспортну таблицю.

Потім згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності u_i + v_j ≤ c_ij (для порожніх клітинок таблиці):

А₁B₂ : u₁ + v₂ = 5 + (–1) = 4 = 4; (4.5)

А₁B₃ : u₁ + v₃ = 5 + (–1) = 4 > 2; (4.6)

А₂B₁ : u₂ + v₁ = 2 + (–1) = 1 < 5; (4.7)

А₂B₂ : u₂ + v₂ = 2 + (–1) = 1 < 3; (4.8)

А₃B₁ : u₃ + v₁ = 2 + (–1) = 1 < 2; (4.9)

А₃B₃ : u₃ + v₃ = 2 + (–1) = 1 < 4. (4.10)

Умова оптимальності не виконується для клітинки А₁B₃. Порушення ₁₃=(u₁+v₃)–c₁₃ = 4 – 2 = 2 записуємо в лівому нижньому кутку відповідної клітинки.

Отже, перший опорний план транспортної задачі неоптимальний. Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці.

4.4 Перехід від одного опорного плану до іншого

Потрібно заповнити клітинку А₁B₃, в якій є єдине порушення умови оптимальності. Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки А₁B₃, та позначаємо вершини циклу почергово знаками «–» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у порожню клітинку А₁B₃ переносимо менше з чисел х_ij, які розміщені в клітинках зі знаком «–». Одночасно це саме число х_ij додаємо до відповідних чисел, що розміщені в клітинках зі знаком «+», та віднімаємо від чисел, що розміщені в клітинках, позначених знаком «–».

У даному разі , тобто . Виконавши перерозподіл перевезень продукції згідно із записаними правилами, дістанемо такі нові значення: для клітинки А₁B₃ — 40 тис.од.продукції, а для А₂B₃ – (60 – 40) = 20 тис.од., а для А₂B₄ – (0+40) = 40 тис.од. Клітинка А₁B₄ звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписуємо у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості плану, тобто дорівнювати (n+m – 1).

Отже, другий опорний план транспортної задачі матиме такий вигляд (табл.4.2).

Таблиця 4.2

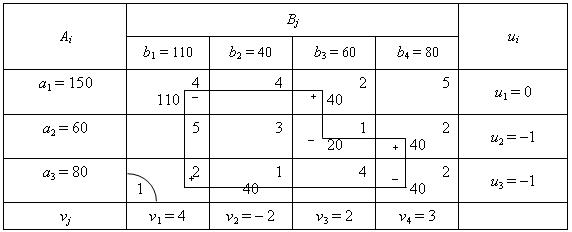
Розрахуємо значення цільової функції відповідно до другого опорного плану задачі:

Z₂ = 4110 + 240 + 120 + 240 + 140 + 240 = 740 (ум.од.). (4.11)

Новий план знову перевіряємо на оптимальність, тобто повторюємо описані раніше дії. Другий опорний план транспортної задачі також неоптимальний (має місце порушення для клітинки А₃B₁). За допомогою побудованого циклу, виконавши перехід до третього опорного плану транспортної задачі, отримуємо табл.4.3.

Таблиця 4.3

Визначимо загальну вартість витрат на транспортування продукції згідно з третім опорним планом:

Z₃ = 490 + 260 + 260 + 220 + 140 + 220 = 720 (ум.од.). (4.12)

Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний. Тому:

. (4.13)

За оптимальним планом перевезень перший замовник отримує 90 тис.од. продукції з першої фабрики та 20 тис.од. — з третьої. Другий споживач задовольняє свій попит за рахунок виробництва та перевезення 40 тис.од. продукції з третьої фабрики і т.д. При цьому загальна вартість перевезень всієї продукції є найменшою і становить 720 ум.од.

Перевіримо правильність рішення задачі за допомогою MS Excel (див.рис.4.1-4.3).

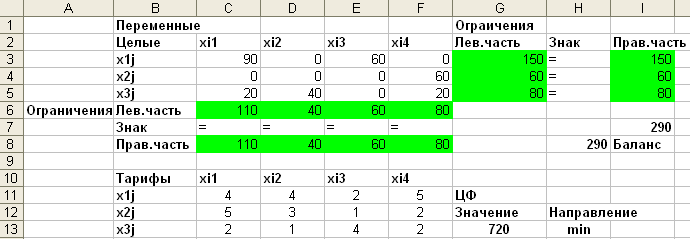
Рисунок 4.1

Рисунок 4.2

Рисунок 4.3

ЗАДАЧА 5

Розв’язати задачу цілочисельного програмування методом Гоморі. Умови завдання наведені нижче.

,

;

;

,

і — цілі числа.

Розв’язання

Розв’язуємо задачу, нехтуючи умовою цілочисловості. Остання симплексна таблиця набуде вигляду табл.5.1.

Таблиця 5.1

Ця симплекс-таблиця дає оптимальний план, але він не є цілочисельним (значення другої змінної є дробовим числом, що не задовольняє початкові умови задачі). Побудуємо для другого рядка наведеної симплексної таблиці додаткове обмеження виду :

. (5.1)

Оскільки , , , то додаткове обмеження (обмеження Гоморі) набуває вигляду:

. (5.2)

Зведемо його до канонічної форми та введемо штучну змінну x₆:

. (5.3)

Приєднавши отримане обмеження до симплексної таблиці (табл.5.1) з умовно-оптимальним планом, дістанемо табл.5.2.

Таблиця 5.2

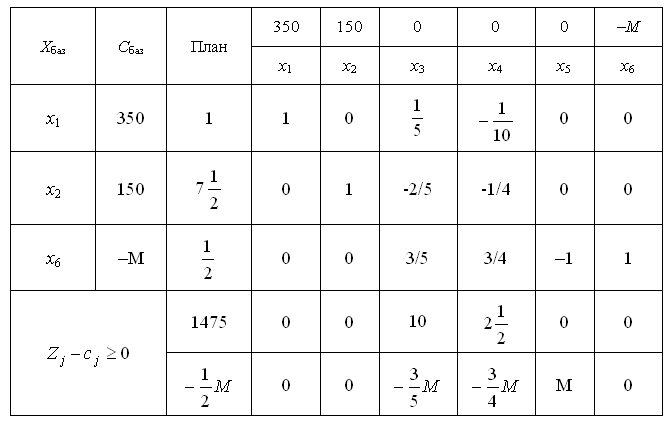
Розв’язавши розширену задачу симплекс-методом, знаходимо цілочисловий оптимальний план: , .

Перевіримо правильність рішення задачі за допомогою MS Excel (див.рис.5.1-5.3).

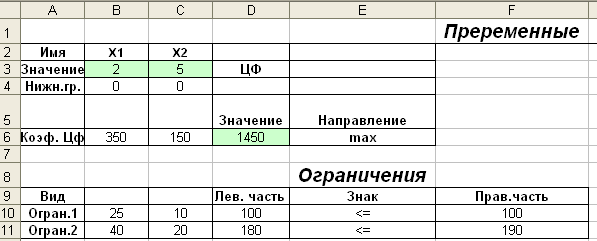
Рисунок 5.1

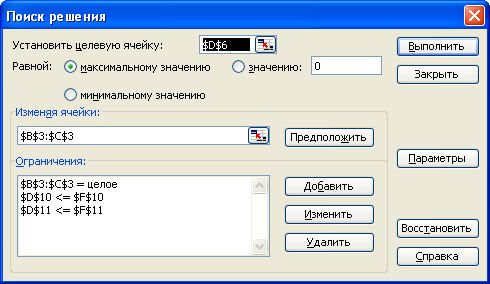
Рисунок 5.2

Рисунок 5.3

СПИСОК ЛІТЕРАТУРИ

1. Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. – К.: КНЕУ, 2003. – 452 с.

2. Курицкий Б.Я. Поиск оптимальных решений средствами Ехсеl 7.0. – СПб.: ВНV, 1997. – 384 с.