
- •Кафедра теоретической и прикладной механики теоретическая механика Учебно-методический комплекс
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •1.2.1. Содержание дисциплины по гос
- •1.2.2. Объем дисциплины и виды учебной работы
- •Раздел I. Статика (40 часов)
- •1.2. Моменты силы. Пара сил (10 часов)
- •1.3. Произвольная система сил (10 часов)
- •1.4. Плоская система сил (10 часов)
- •Раздел 2. Кинематика (60 часов)
- •2.1. Кинематика точки (13 часов)
- •2.2. Простейшие движения твердого тела (9 часов)
- •2.3. Сложное движение точки (15 часов)
- •2.4. Плоское движение твердого тела (15 часов)
- •2.5. Сферическое движение твердого тела. Общий случай движения свободного твердого тела (8 часов)
- •Раздел 3. Динамика (100 часов)
- •3.1. Дифференциальные уравнения движения материальной точки (10 часов)
- •3.2. Прямолинейные колебания материальной точки (12 часов)
- •3.3. Введение в динамику механической системы. Теорема об изменении количества движения системы и о движении центра масс системы (8 часов)
- •3.4. Теорема об изменении кинетического момента системы относительно неподвижных центра и осей (10 часов)
- •3.5. Теорема об изменении кинетической энергии системы (10 часов)
- •3.6. Динамика плоского движения твердого тела (10 часов)
- •3.7. Основы кинетостатики (10 часов)
- •3.8. Введение в аналитическую механику (8 часов)
- •3.9. Принцип возможных перемещений (11 часов)
- •3.10. Общее уравнение динамики. Уравнения Лагранжа второго рода (11 часов)
- •3.11. Элементарная теория гироскопа (13 часов)
- •3.12. Основы теории удара (17 часов)
- •Заключение
- •2.2. Тематический план дисциплины
- •2.2.1. Тематический план дисциплины для студентов очной формы обучения
- •2.2.2. Тематический план дисциплины для студентов очно-заочной формы обучения
- •2.2.3. Тематический план дисциплины для студентов заочной формы обучения
- •2.2.4. Тематический план дисциплины для студентов очной формы обучения
- •2.2.5. Тематический план дисциплины для студентов очно-заочной формы обучения
- •2.2.6. Тематический план дисциплины для студентов заочной формы обучения
- •2.4.1.2. Практические занятия (очно-заочная форма обучения)
- •2.4.1.3. Практические занятия (заочная форма обучения)
- •2.4.2. Практические занятия
- •2.4.2.2. Практические занятия (очно-заочная форма обучения)
- •2.4.2.3. Практические занятия (заочная форма обучения)
- •2.5. Временной график изучения дисциплины
- •2.5.1. Временной график изучения дисциплины «Теоретическая механика»
- •2.5.2. Временной график изучения дисциплины «Теоретическая механика»
- •2.6. Балльно-рейтинговая система оценки знаний
- •3. Информационные ресурсы дисциплины
- •3.1. Библиографический список
- •3.2. Опорный конспект по дисциплине Введение
- •Раздел 1. Статика
- •1.1. Введение в механику
- •1.1.1. Некоторые основные понятия и определения
- •1.1.2. Основные законы механики
- •1.1.3. Свободные и несвободные тела. Связи и реакции связей
- •1.2. Моменты силы. Пара сил
- •1.2.1.Предмет статики
- •1.2.2. Условия и уравнения равновесия материальной точки
- •1.2.3. Момент силы относительно точки
- •1.2.4. Момент силы относительно оси
- •1.2.5. Пара сил и ее свойства
- •1.3. Произвольная система сил
- •1.3.1. Приведение силы к данному центру
- •1.3.2. Основная теорема статики
- •1.3.3. Определение модулей и направлений главного вектора и главного момента
- •1.3.4. Уравнения равновесия произвольной системы сил.
- •1.4. Плоская система сил
- •1.4.1. Уравнения равновесия плоской системы сил
- •1.4.2. Пример решения задачи на равновесие твердого тела под действием плоской системы сил
- •1.4.3. Равновесие системы тел
- •1.4.4. Пример решения задачи на равновесие твердого тела под действием произвольной системы сил
- •Раздел 2. Кинематика
- •2.1. Кинематика точки
- •2.1.1. Кинематические способы задания движения точки
- •2.1.2. Скорость точки
- •2.1.3. Ускорение точки
- •2.1.4. Естественные оси
- •2.1.5. Проекции вектора ускорения точки на естественные оси
- •2.1.6. Пример решения задачи на кинематику точки
- •2.2. Простейшие движения твердого тела
- •2.2.1. Поступательное движение твердого тела
- •2.2.2. Вращение твердого тела вокруг неподвижной оси и кинематические характеристики этого движения
- •2.2.3. Скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси
- •2.2.4. Векторные формулы для кинематических характеристик вращающегося твердого тела
- •2.2.5. Пример решения задачи на вращение твердого тела вокруг неподвижной оси
- •Раздел 3. Динамика
- •3.1. Динамика материальной точки
- •3.1.1. Основное уравнение динамики материальной точки в декартовых и естественных координатах
- •3.1.2. Две основные задачи динамики материальной точки
- •3.1.3. Инерциальные системы отсчета
- •3.2. Прямолинейные колебания материальной точки
- •3.2.1. Свободные гармонические колебания материальной точки
- •3.2.2. Пример решения задачи на свободные колебания точки
- •3.2.2. Свободные затухающие колебания материальной точки
- •3.2.3. Вынужденные колебания материальной точки
- •3.3. Теоремы об изменении количества движения и о движении центра масс механической системы
- •3.3.1. Механическая система
- •3.3.2. Количество движения материальной точки и системы
- •3.3.3. Теорема об изменении количества движения системы
- •3.3.4. Теорема о движении центра масс системы
- •3.3.5. Пример решения задачи на теорему о движении центра масс
- •3.4. Теорема об изменении кинетического момента механической системы относительно неподвижных центра и оси
- •3.4.1. Момент количества движения материальной точки относительно центра и оси
- •3.4.2. Кинетический момент системы относительно центра и оси
- •3.4.3. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси
- •3.4.4. Осевые моменты инерции однородных тел простейшей геометрической формы
- •3.4.5. Теоремы об изменении кинетического момента системы относительно неподвижных центра и оси
- •3.4.6. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
- •3.4.7. Пример решения задач на теорему об изменении кинетического момента системы
- •3.5. Теорема об изменении кинетической энергии механической системы
- •3.5.1. Кинетическая энергия материальной точки, твердого тела и механической системы
- •3.5.2. Кинетическая энергия твердого тела
- •3.5.3. Работа и мощность силы
- •3.5.4. Работа силы тяжести и силы упругости
- •3.5.5. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси
- •3.5.6. Теорема об изменении кинетической энергии материальной точки
- •3.5.7. Теорема об изменении кинетической энергии системы
- •3.5.8. Потенциальное силовое поле
- •3.5.9. Закон сохранения механической энергии
- •3.5.10. Пример решения задачи на теорему об изменении кинетической энергии механической системы
- •Заключение
- •3.3. Глоссарий (краткий словарь терминов)
- •4. Блок контроля освоения дисциплины
- •4.1. Задания на контрольные работы и методические указания к их выполнению
- •4.1.1. Общие указания
- •4.1.2. Указания к выполнению контрольной работы 1 (Таблица 1)
- •4.1.3. Указания к выполнению контрольной работы 2 (Таблица 2)
- •4.1.4. Указания к выполнению контрольной работы 3 (Таблица 3)
- •4.1.5. Указания к выполнению контрольной работы 4 (Таблица 4)
- •4.1.6. Указания к выполнению контрольной работы 3 (Таблица 5)
- •4.1.7. Указания к выполнению контрольной работы 4 (Таблица 6)
- •4.2. Тестовые задания текущего контроля
- •4.3. Итоговый контроль. Вопросы к экзамену
4.2. Тестовые задания текущего контроля
Тест №1
1. Дайте определение материальной точки.
A. Материальное тело малых размеров (атом, молекула).
B. Геометрическая точка.
C. Материальное тело, размерами которого можно пренебречь в условиях конкретной задачи.
D. Материальное тело, масса которого сосредоточена в одной его точке.
2. Сила, приложенная к свободной материальной точке, сообщает ей.
A. Скорость.
B. Ускорение.
C. Замедление.
D. Ничего не сообщает.
3.
Сравните по модулю силы
и
,
если
![]() ,
,
![]() .
.
 A.
A.
![]()
B.
![]()
С.
![]()
D.
![]()
4.
К плоской фигуре (рис. 1) приложена система
сил
![]() ,
модули которых равны
,
модули которых равны
![]() ;
;
![]() .
Какая из этих сил дает проекцию на ось
,
равную
.
Какая из этих сил дает проекцию на ось
,
равную
![]() ?
?
A.
B.
С.
![]()
D.
![]() .
.
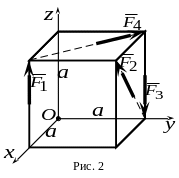 5.
К вершинам куба со стороной
5.
К вершинам куба со стороной
![]() (рис. 2) приложены силы
,
модули которых равны
(рис. 2) приложены силы
,
модули которых равны
![]() .
Какая из сил дает момент относительно
оси
,
равный
.
Какая из сил дает момент относительно
оси
,
равный
![]() ?
?
A.
![]()
B.
![]()
С.
![]()
D.
![]()
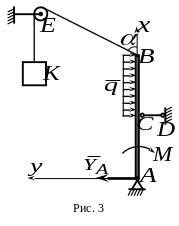 6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
![]() и парой сил с моментом
и парой сил с моментом
![]() (рис.3). К концу балки прикреплен трос
(рис.3). К концу балки прикреплен трос
![]() ,
перекинутый через блок
.
К концу троса подвешен груз
весом
,
перекинутый через блок
.
К концу троса подвешен груз
весом
![]() .
.
Какой
из ответов соответствует проекции
реакции
на ось
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ?
?
A.
![]()
B.
![]()
С.
![]()
D.
![]() .
.
7.
Коленчатый вал нагружен силами
![]() ,
,
![]() ,
,
![]() ,
причем
,
причем
![]() ,
,
![]() ,
параллельна плоскости
,
параллельна плоскости
![]() (рис.4). Колено – квадрат со стороной
(рис.4). Колено – квадрат со стороной
![]() ,
который лежит в плоскости
,
который лежит в плоскости
![]() .
Плоскость диска
с радиусом
.
Плоскость диска
с радиусом
![]() перпендикулярна оси
;
перпендикулярна оси
;
![]() ,
,
![]() ,
,
![]() ,
(
,
(![]() ).
Какой из ответов соответствует проекции
составляющей реакции
на ось
).
Какой из ответов соответствует проекции
составляющей реакции
на ось
![]() ?
?
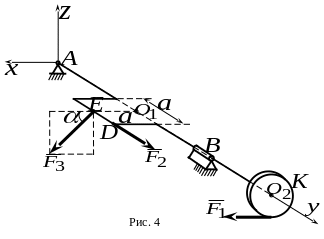
A.
B.
![]()
С.
![]()
D.
![]() .
.
Тест №2
1. Дайте определение инерции (или инертности) материальной точки.
A. Это врожденное свойство материи.
B. Если материальной точке дать толчок, то она будет двигаться прямолинейно и равномерно.
C. Под инерцией понимают состояние покоя, либо прямолинейного и равномерного движения изолированной материальной точки.
D. Материальную точку нельзя вывести из состояния покоя, пока на нее не подействует другое тело.
2.
Сравните по модулю силы
и
,
если
![]() ,
,
![]() .
.
A.
B.
![]()
С.
D.
![]()
3.
Определить модуль равнодействующей
двух сил
и
,
приложенных в точке, если
![]() ,
а угол между ними
,
а угол между ними
![]() .
.
 A.
A.
![]()
B.
![]()
С.
![]()
D.
![]() 4
4
4.
К плоской фигуре (рис. 5) приложена система
сил
,
модули которых равны
;
.
Какая из этих сил дает проекцию на ось
,
равную
![]() ?
?
A.
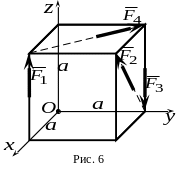 B.
B.
С.
D. .
5.
К вершинам куба со стороной
(рис. 6) приложены силы
,
модули которых равны
.
Какая из сил дает момент относительно
оси
,
равный
![]() ?
?
A. B.
С. D.
 6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
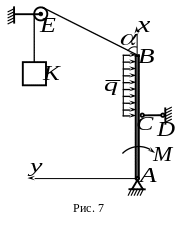
(рис. 7). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
Какой из ответов соответствует проекции
реакции
на ось
,
если
,
,
,
,
?
6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
(рис. 7). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
Какой из ответов соответствует проекции
реакции
на ось
,
если
,
,
,
,
?
A.
B.
С.
D.
7.
Коленчатый вал нагружен силами
,
,
,
причем
,
,
параллел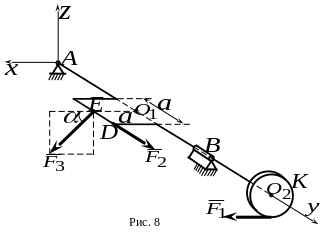 ьна
плоскости
(рис.8). Колено – квадрат со стороной
,
который лежит в плоскости
.
Плоскость диска
с радиусом
перпендикулярна оси
;
,
,
,
(
).
Определить модуль силы
.
ьна
плоскости
(рис.8). Колено – квадрат со стороной
,
который лежит в плоскости
.
Плоскость диска
с радиусом
перпендикулярна оси
;
,
,
,
(
).
Определить модуль силы
.
A.
B.
![]()
С.
D.
![]() .
.
Тест №3
1. Дайте определение уравновешенной системы сил.
A. Под действием уравновешенной системы сил материальное тело всегда находится в равновесии.
B. Уравновешенная система сил приводит материальное тело в состояние покоя.
C. Уравновешенной называется такая система сил, которая действуя на свободную материальную точку, находившуюся в состоянии покоя, не выводит ее из этого состояния.
D. Условия равновесия сил всегда являются условиями равновесия материальных тел.
2. Что является простейшей уравновешенной системой сил?.
A. Простейшей уравновешенной системой сил называются две силы, равные по модулю.
B. Простейшей уравновешенной системой сил называются две силы, параллельные друг другу и равные по модулю.
C. Простейшей уравновешенной системой сил называются такие две силы, которые будучи приложенными к покоящейся материальной точке, не выведут ее из этого состояния.
D. Простейшей уравновешенной системой сил называются две силы, равные по модулю и направленные в противоположные стороны вдоль одной прямой.
3.
Сравните по модулю силы
и
,
если
![]() ,
,
![]() .
.
A.
B.
С.
D.
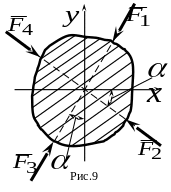 4.
К плоской фигуре (рис. 9) приложена система
сил
,
модули которых равны
;
.
Какая из этих сил дает проекцию на ось
,
равную
?
4.
К плоской фигуре (рис. 9) приложена система
сил
,
модули которых равны
;
.
Какая из этих сил дает проекцию на ось
,
равную
?
A.
B.
С.
D. .
5.
К вершинам куба со стороной
(рис. 10) приложены силы
,
модули которых равны 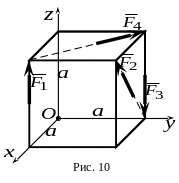 .
Какая из сил дает момент относительно
оси
,
равный
.
Какая из сил дает момент относительно
оси
,
равный
![]() ?
?
A.
B.
С.
D.
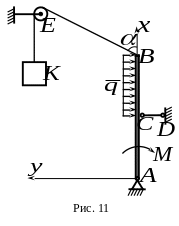
6. Балка нагружена равномерно распределенной нагрузкой интенсивностью и парой сил с моментом (рис.11). К концу балки прикреплен трос , перекинутый через блок . К концу троса подвешен груз весом . Какой из ответов соответствует проекции реакции стержня , если , , ?
A.
B.
С.
D.
7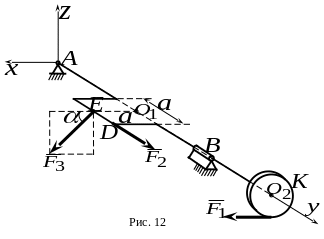 .
Коленчатый вал нагружен силами
,
,
,
причем
,
,
параллельна плоскости
(рис.12). Колено – квадрат со стороной
,
который лежит в плоскости
.
Плоскость диска
с радиусом
перпендикулярна оси
;
,
,
,
(
).
Определить проекцию составляющей
реакции
на ось
.
.
Коленчатый вал нагружен силами
,
,
,
причем
,
,
параллельна плоскости
(рис.12). Колено – квадрат со стороной
,
который лежит в плоскости
.
Плоскость диска
с радиусом
перпендикулярна оси
;
,
,
,
(
).
Определить проекцию составляющей
реакции
на ось
.
A.
B.
![]()
С.
D.
![]()
Тест №4
1. Сила, приложенная к свободной материальной точке, сообщает ей.
A. Скорость.
B. Ускорение.
C. Замедление.
D. Ничего не сообщает.
2.
Сравните по модулю силы
и
,
если
![]() ,
,
![]() .
.
A.
B.
С.
D.
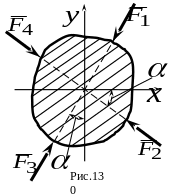 3.
Определить модуль равнодействующей
двух сил
и
,
приложенных в точке, если
,
а угол между ними
3.
Определить модуль равнодействующей
двух сил
и
,
приложенных в точке, если
,
а угол между ними
![]() .
.
A.
B.
![]()
С.
D.
![]()
4. К плоской фигуре (рис. 13) приложена система сил , модули которых равны ; .
Какая из этих сил дает проекцию на ось , равную ?
A.
B.
 С.
С.
D. .
5. К вершинам куба со стороной (рис. 14) приложены силы , модули которых равны . Какая из сил дает момент относительно оси , равный нулю?
A.
B.
С.
D. .
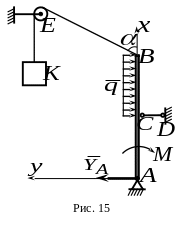 6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
(рис.15). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
(рис.15). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
Какой
из ответов соответствует проекции
реакции
на ось
,
если
![]() ,
,
,
(
,
)?
,
,
,
(
,
)?
A.
B.
С.
D. .
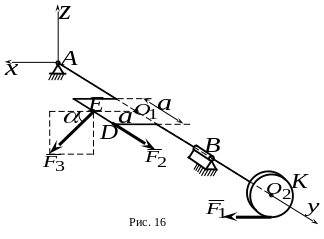
7.
Коленчатый вал нагружен силами
,
,
,
причем
,
,
параллельна плоскости
(рис.16). Колено – квадрат со стороной
,
который лежит в плоскости
.
Плоскость диска
с радиусом
перпендикулярна оси
;
,
,
,
(
).
Какой из ответов соответствует проекции
составляющей реакции
на ось
![]() ?
?
A.
B.
С.
![]()
D.
Тест №5
1. Укажите первую или основную форму системы уравнений равновесия для плоской системы сил, действующих на твердое тело.
A.
![]()
B.
![]()
С.
![]()
D.
![]()
2.
Сравните по модулю силы
и
,
если
![]() ,
,
![]() .
.
A.
B.
С.
D.
3. Определить модуль равнодействующей двух сил и , приложенных в точке, если , а угол между ними .
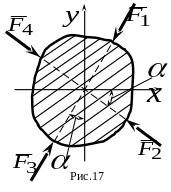 A.
A.
B.
С.
D.
![]()
4. К плоской фигуре (рис. 17 приложена система сил , модули которых равны ; . Какая из этих сил дает проекцию на ось , равную ?
A.
B.
С.
D. .
5.
К вершинам куба со стороной
(рис. 18) приложены силы 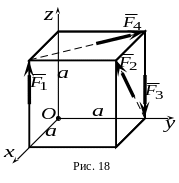 ,
модули которых равны
,
модули которых равны
![]() .
Какая из сил дает момент относительно
оси
,
равный
.
Какая из сил дает момент относительно
оси
,
равный
![]() ?
?
A.
B.
С.
D. .
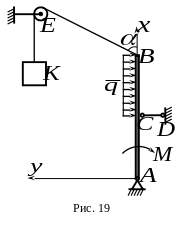 6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
(рис.19). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
(рис.19). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
Какой из ответов соответствует проекции реакции на ось , если , , , , ?
A.
B.
![]()
С.
D.
![]() .
.
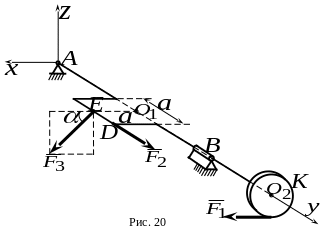
7. Коленчатый вал нагружен силами , , , причем , , параллельна плоскости (рис.20). Колено – квадрат со стороной , который лежит в плоскости . Плоскость диска с радиусом перпендикулярна оси ; , , , ( ). Какой из ответов соответствует проекции составляющей реакции на ось ?
A.
B.
С.
D.
Тест №6
1. Какой принцип механики позволяет изучать механику несвободных материальных тел?
A. Принцип отвердевания.
B. Принцип независимости действия сил.
С. Принцип освобождаемости от связей.
D. Принцип относительности механики.
2.
Сравните по модулю силы
и
,
если
![]() ,
,
![]() .
.
A.
B.
С.
D.
3.
Определить модуль равнодействующей
двух сил
и
,
приложенных в точке, если
![]() ,
а угол между ними
.
,
а угол между ними
.
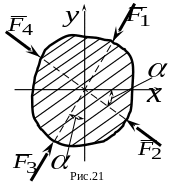
A.
![]()
B.
![]()
С.
D.
4.
К плоской фигуре (рис. 21) приложена
система сил
,
модули которых равны
![]() ;
.
Какая из этих сил дает проекцию на ось
,
равную
;
.
Какая из этих сил дает проекцию на ось
,
равную
![]() ?
?
A.
B.
С.
D. .
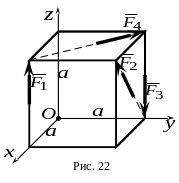 5.
К вершинам куба со стороной
(рис. 22) приложены силы
,
модули которых равны
.
Какая из сил дает момент относительно
оси
,
равный
5.
К вершинам куба со стороной
(рис. 22) приложены силы
,
модули которых равны
.
Какая из сил дает момент относительно
оси
,
равный
![]() ?
?
A. B.
С. D. .
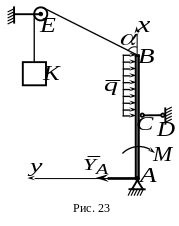 6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
(рис.23). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
6.
Балка
нагружена равномерно распределенной
нагрузкой интенсивностью
и парой сил с моментом
(рис.23). К концу балки прикреплен трос
,
перекинутый через блок
.
К концу троса подвешен груз
весом
.
Какой из ответов соответствует проекции реакции на ось , если , , , ( , )?
A.
B.
![]()
С.
D. .
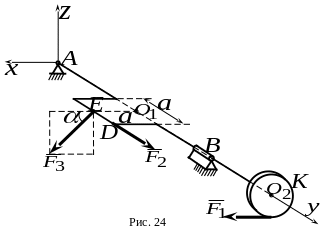
7. Коленчатый вал нагружен силами , , , причем , , параллельна плоскости (рис.24). Колено – квадрат со стороной , который лежит в плоскости . Плоскость диска с радиусом перпендикулярна оси ; , , , ( ). Какой из ответов соответствует проекции составляющей реакции на ось ?
A.
B.
![]()
С.
D.
Тест №7
1. Дайте определение материальной точки.
А. Геометрическая точка.
B. Материальное тело малых размеров (атом, молекула).
C. Материальное тело, масса которого сосредоточена в одной его точке.
D. Материальное тело, размерами которого можно пренебречь в условиях конкретной задачи.
2.
Сравните по модулю силы
и
,
если
![]() ,
,
![]() .
.
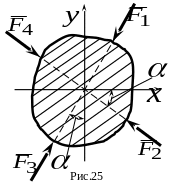 A.
A.
B.
С.
D.
3.
К плоской фигуре (рис. 25) приложена
система сил
,
модули которых равны
![]() ;
.
Какая из этих сил дает проекцию на ось
,
равную
;
.
Какая из этих сил дает проекцию на ось
,
равную
![]() ?
?
A.
B.
С.
D. .
4.
Определить модуль равнодействующей
двух сил
и
,
приложенных в точке, если
,
а угол между ними
![]() .
.
A.
B.
С.
![]()
D.
![]()
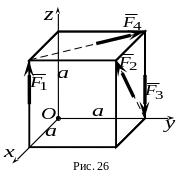
5. К вершинам куба со стороной (рис. 26) приложены силы , модули которых равны . Какая из сил дает момент относительно оси , равный нулю?
A.
B.
С.
D. .
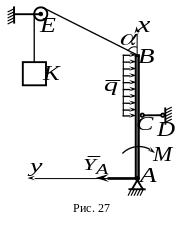
6. Балка нагружена равномерно распределенной нагрузкой интенсивностью и парой сил с моментом (рис.27). К концу балки прикреплен трос , перекинутый через блок . К концу троса подвешен груз весом .
Какой
из ответов соответствует проекции
реакции стержня
![]() ,
если
,
,
,
,
?
,
если
,
,
,
,
?
A. B.
С. D. .
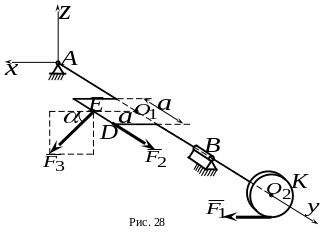
7. Коленчатый вал нагружен силами , , , причем , , параллельна плоскости (рис.28). Колено – квадрат со стороной , который лежит в плоскости . Плоскость диска с радиусом перпендикулярна оси ; , , , ( ). Какой из ответов соответствует проекции составляющей реакции на ось ?
A.
B.
С.
D.
Тест №8
1.
Если
![]() ,
то какое движение совершает точка?
,
то какое движение совершает точка?
А. Точка движется равномерно по любой траектории.
B. Точка движется неравномерно и прямолинейно.
C. Точка движется равномерно и прямолинейно.
D. Точка движется неравномерно по любой траектории.
2.
Точка движется по закону
![]() .
Какой из ответов соответствует модулю
скорости точки
в момент
.
Какой из ответов соответствует модулю
скорости точки
в момент
![]() ?
Построить траекторию точки и показать
вектор скорости
?
Построить траекторию точки и показать
вектор скорости
![]() (
- в
,
(
- в
,
![]() - в
).
- в
).
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
3.
Зубчатое колесо I вращается против хода
часовой стрелки вокруг неподвижной
точки
по закону
![]() и вращает колесо II вокруг неподвижной
оси
и вращает колесо II вокруг неподвижной
оси
![]() ,
а последнее приводит в движение рейку
(рис. 29).
,
а последнее приводит в движение рейку
(рис. 29).
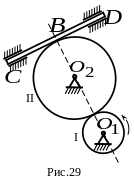 Какой
из ответов соответствует модулю ускорения
рейки
в момент времени
Какой
из ответов соответствует модулю ускорения
рейки
в момент времени
![]() ?
Радиусы колес:
?
Радиусы колес:
![]() ,
,
![]() (
- в
(
- в
![]() ,
- в
).
,
- в
).
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
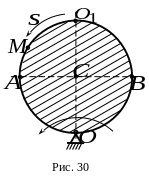
4.
По ободу диска радиусом
![]() (рис.30) от точки
движется точка
по закону
(рис.30) от точки
движется точка
по закону
![]() (
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
![]() (
- в
,
- в
).
(
- в
,
- в
).
Какой
из ответов соответствует модулю
абсолютной скорости
![]() точки
в момент времени
,
если
точки
в момент времени
,
если
![]() ,
а точка
находится в положении
?
,
а точка
находится в положении
?
 А.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
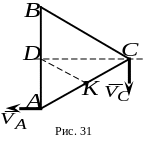
5.
Равносторонний треугольник со стороной
![]() движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
![]() ;
;
![]() ,
а вектор скорости точки
:
,
а вектор скорости точки
:
![]() (рис. 31).
(рис. 31).
Какой
из ответов соответствует модулю скорости
точки
,
если
![]() ?
?
А.
![]() .
.
B. .
C.
![]() .
.
D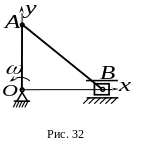 .
.
.
.
6.
В кривошипно-ползунном механизме
кривошип
![]() вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
![]() .
.
![]() ,
,
![]() (рис.32).
(рис.32).
Определить модуль ускорения ползуна в указанном положении механизма.
А.
![]() . B.
.
. B.
.
C.
![]() . D.
. D.
![]() .
.
Тест №9
1.
Если
![]() ,
то какое движение совершает точка?
,
то какое движение совершает точка?
А. Точка движется неравномерно и прямолинейно.
B. Точка движется равномерно по любой траектории.
C. Точка движется равномерно и прямолинейно.
D. Точка движется неравномерно по любой траектории.
2.
Точка движется по закону
![]() .
Какой из ответов соответствует модулю
скорости точки
в начальный момент времени (
.
Какой из ответов соответствует модулю
скорости точки
в начальный момент времени (![]() - в
,
- в
)?
- в
,
- в
)?
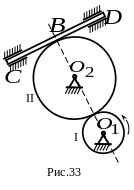
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
3. Зубчатое колесо I вращается против хода часовой стрелки вокруг неподвижной точки по закону и вращает колесо II вокруг неподвижной оси , а последнее приводит в движение рейку (рис. 33).
Какой из ответов соответствует модулю скорости рейки в момент времени ? Радиусы колес: , ( - в , - в ).
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
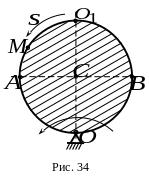
4. По ободу диска радиусом (рис.34) от точки движется точка по закону ( - в , - в ) Одновременно диск вращается против хода часовой стрелки вокруг неподвижной оси в плоскости чертежа по закону ( - в , - в ).
Какой из ответов соответствует модулю абсолютной скорости точки в момент времени , если , а точка находится в положении ?
 А.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D. .
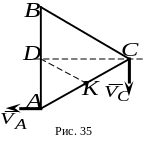
5.
Равносторонний треугольник со стороной
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
![]() ;
,
а вектор скорости точки
:
(рис. 35).
;
,
а вектор скорости точки
:
(рис. 35).
К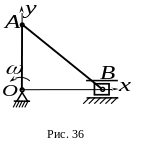 акой
из ответов соответствует модулю скорости
точки
,
если
?
акой
из ответов соответствует модулю скорости
точки
,
если
?
А. .
B. .
C. .
D. .
6.
В кривошипно-ползунном механизме
(рис.36) кривошип
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
![]() .
,
.
,
Определить модуль ускорения ползуна в указанном положении механизма.
А.
![]() . B.
.
. B.
.
C. . D. .
Тест №10
1.
Если
,
причем
![]() ,
то какое движение совершает точка?
,
то какое движение совершает точка?
А. Точка движется равномерно по любой траектории.
B. Точка движется равноускоренно и прямолинейно.
C. Точка движется равнозамедленно и прямолинейно.
D. Точка движется равноускоренно по любой траектории.
2.
Точка движется по закону
![]() .
Какой из ответов соответствует модулю
скорости точки
в момент времени
(
- в
,
- в
)?
Построить траекторию и показать вектор
.
.
Какой из ответов соответствует модулю
скорости точки
в момент времени
(
- в
,
- в
)?
Построить траекторию и показать вектор
.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
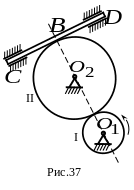 3.
Зубчатое колесо I вращается против хода
часовой стрелки вокруг неподвижной
точки
по закону
и вращает колесо II вокруг неподвижной
оси
,
а последнее приводит в движение рейку
(рис. 37).
3.
Зубчатое колесо I вращается против хода
часовой стрелки вокруг неподвижной
точки
по закону
и вращает колесо II вокруг неподвижной
оси
,
а последнее приводит в движение рейку
(рис. 37).
Какой из ответов соответствует модулю ускорения рейки в момент времени ? Радиусы колес: , ( - в , - в ).
А. .
B. .
C. .
D. .
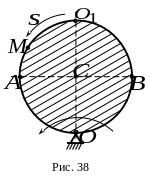 4.
По ободу диска радиусом
4.
По ободу диска радиусом
![]() (рис.38) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
(рис.38) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
Какой из ответов соответствует модулю абсолютной скорости точки в момент времени , если , а точка находится в положении ?
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
 5.
Равносторонний треугольник со стороной
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
5.
Равносторонний треугольник со стороной
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
![]() ;
,
а вектор скорости точки
:
(рис. 39).
;
,
а вектор скорости точки
:
(рис. 39).
Какой из ответов соответствует модулю скорости точки , если ?
А. . B. .
C.
![]() . D.
.
. D.
.
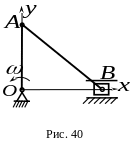
6. В кривошипно-ползунном механизме кривошип вращается равномерно вокруг неподвижной оси , перпендикулярной плоскости чертежа, с угловой скоростью . , (рис.40).
Определить
модуль вращательного ускорения
![]() точки
при вращении ее вокруг полюса
в
указанном положении механизма.
точки
при вращении ее вокруг полюса
в
указанном положении механизма.
А. . B. .
C. . D. .
Тест №11
1.
Если
,
![]() ,
то какое движение совершает точка?
,
то какое движение совершает точка?
А. Точка движется равномерно по любой траектории.
B. Точка движется неравномерно прямолинейно.
C. Точка движется равномерно по криволинейной траектории.
D. Точка движется неравномерно по любой траектории.
2.
Точка движется по закону
![]() .
Какой из ответов соответствует модулю
касательного ускорения точки
в момент времени
(
- в
,
- в
)?
Построить траекторию движения точки и
указать вектор
.
.
Какой из ответов соответствует модулю
касательного ускорения точки
в момент времени
(
- в
,
- в
)?
Построить траекторию движения точки и
указать вектор
.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D. .
3.
Зубчатое колесо I вращается против хода
ч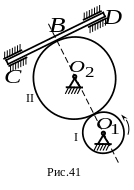 асовой
стрелки вокруг неподвижной точки
по закону
и вращает колесо II вокруг неподвижной
оси
,
а последнее приводит в движение рейку
(рис. 41).
асовой
стрелки вокруг неподвижной точки
по закону
и вращает колесо II вокруг неподвижной
оси
,
а последнее приводит в движение рейку
(рис. 41).
Какой
из ответов соответствует модулю ускорения
рейки
в момент времени
![]() ?
Радиусы колес:
,
(
- в
,
- в
).
?
Радиусы колес:
,
(
- в
,
- в
).
А. .
B. .
C. .
D. .
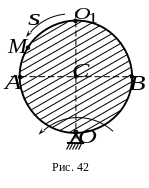
4.
По ободу диска радиусом
![]() (рис.42) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
(рис.42) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
Какой из ответов соответствует модулю абсолютной скорости точки в момент времени , если , а точка находится в положении ?
 А.
А.
![]() .
.
B.
![]() .
.
C. .
D. .
5.
Равносторонний треугольник со ст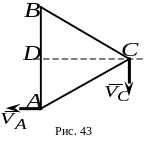 ороной
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
;
,
а вектор скорости точки
:
(рис. 43).
ороной
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
;
,
а вектор скорости точки
:
(рис. 43).
Какой из ответов соответствует модулю скорости точки ?
А. .
B. .
C. .
D.
![]() .
.
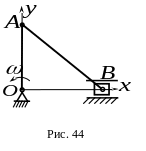
6.
В кривошипно-ползунном механизме
кривошип
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
![]() .
,
(рис.44).
.
,
(рис.44).
Определить модуль ускорения ползуна в указанном положении механизма.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
Тест №12
1.
Если
![]() ,
то какое движение совершает точка?
,
то какое движение совершает точка?
А. Точка движется равномерно по любой траектории.
B. Точка движется неравномерно и прямолинейно.
C. Точка движется равномерно и прямолинейно.
D. Точка движется неравномерно по любой траектории.
2.
Точка движется по закону
![]() .
Какой из ответов соответствует модулю
скорости точки
в момент
?
Построить траекторию точки и показать
вектор скорости
(
- в
,
- в
).
.
Какой из ответов соответствует модулю
скорости точки
в момент
?
Построить траекторию точки и показать
вектор скорости
(
- в
,
- в
).
А. . B. .
C. . D. .
3. Зубчатое колесо I вращается против хода часовой стрелки вокруг неподвижной точки по закону и вращает колесо II вокруг неподвижной оси , а последнее приводит в движение рейку (рис. 45).
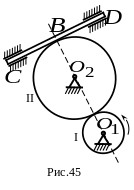 Какой
из ответов соответствует модулю скорости
рейки
в момент времени
?
Радиусы колес:
,
(
- в
,
- в
).
Какой
из ответов соответствует модулю скорости
рейки
в момент времени
?
Радиусы колес:
,
(
- в
,
- в
).
А. .
B. .
C. .
D.
![]() .
.
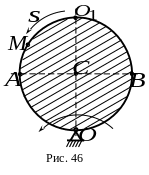 4.
По ободу диска радиусом
(рис.46) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
4.
По ободу диска радиусом
(рис.46) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
Какой из ответов соответствует модулю абсолютной скорости точки в момент времени , если , а точка находится в положении ?
А. . B. .
C.
![]() . D.
. D.
![]() .
.
5.
Равносторонний треугольник со стор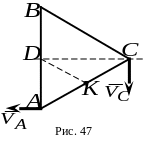 оной
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
оной
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
![]() ;
,
а вектор скорости точки
:
(рис. 47).
;
,
а вектор скорости точки
:
(рис. 47).
Какой из ответов соответствует модулю скорости точки , если ?
А.
![]() .
.
B. .
C.
![]() .
.
D.
![]() .
.
6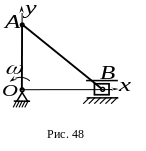 .
В кривошипно-ползунном механизме
кривошип
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
.
,
(рис.48).
.
В кривошипно-ползунном механизме
кривошип
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
.
,
(рис.48).
Определить модуль ускорения ползуна в указанном положении механизма.
А.
![]() .
.
B. .
C. .
D.
![]() .
.
Тест №13
1.
Если
![]() ,
то какое движение совершает точка?
,
то какое движение совершает точка?
А. Точка движется неравномерно по криволинейной траектории.
B. Точка движется неравномерно и прямолинейно.
C. Точка движется равномерно и прямолинейно.
D. Точка движется равномерно по любой траектории.
2. Точка движется по закону . Какой из ответов соответствует модулю нормального ускорения точки в момент ? Построить траекторию точки и показать вектор ускорения ( - в , - в ).
А.
![]() . B.
.
. B.
.
C.
. D.
![]() .
.
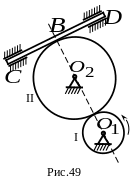 3.
Зубчатое колесо I вращается против хода
часовой стрелки вокруг неподвижной
точки
по закону
и вращает колесо II вокруг неподвижной
оси
,
а последнее приводит в движение рейку
(рис. 49).
3.
Зубчатое колесо I вращается против хода
часовой стрелки вокруг неподвижной
точки
по закону
и вращает колесо II вокруг неподвижной
оси
,
а последнее приводит в движение рейку
(рис. 49).
Какой из ответов соответствует модулю скорости рейки в момент времени ? Радиусы колес: , ( - в , - в ).
А.
![]() . B.
.
. B.
.
C.
. D.
![]() .
.
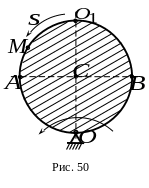 4.
По ободу диска радиусом
(рис.50) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
4.
По ободу диска радиусом
(рис.50) от точки
движется точка
по закону
(
- в
,
- в
)
Одновременно диск вращается против
хода часовой стрелки вокруг неподвижной
оси
в плоскости чертежа по закону
(
- в
,
- в
).
Какой из ответов соответствует модулю абсолютной скорости точки в момент времени , если , а точка находится в положении ?
А.
![]() . B.
.
. B.
.
C.
![]() . D.
. D.
![]() .
.
5.
Равносторонний треугольник со ст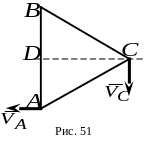 ороной
ороной
![]() движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
;
,
а вектор скорости точки
:
(рис. 51).
движется в плоскости чертежа так, что
в данный момент времени скорость точки
равна
;
,
а вектор скорости точки
:
(рис. 51).
Какой из ответов соответствует модулю скорости точки ?
А. .
B. .
C.
![]() .
.
D. .
6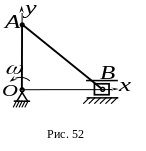 .
В кривошипно-ползунном механизме
кривошип
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
.
,
.
В кривошипно-ползунном механизме
кривошип
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
.
,
![]() (рис.52).
(рис.52).
Определить модуль ускорения ползуна в указанном положении механизма.
А. .
B.
![]() .
.
C.
![]() .
.
D. .
Тест №14
1.
Если
![]() ,
то какое движение совершает точка?
,
то какое движение совершает точка?
А. Точка движется равномерно по криволинейной траектории.
B. Точка движется неравномерно и прямолинейной траектории.
C. Точка движется равномерно и прямолинейно.
D. Точка движется неравномерно по любой траектории.
2.
Точка движется по закону
![]() .
Какой из ответов соответствует модулю
скорости точки
в момент
?
Построить траекторию точки и показать
вектор скорости
(
- в
,
- в
).
.
Какой из ответов соответствует модулю
скорости точки
в момент
?
Построить траекторию точки и показать
вектор скорости
(
- в
,
- в
).
А.
![]() .
.
B.
.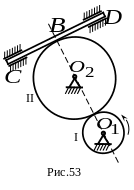
C.
![]() .
.
D.
![]() .
.
3. Зубчатое колесо I вращается против хода часовой стрелки вокруг неподвижной точки по закону и вращает колесо II вокруг неподвижной оси , а последнее приводит в движение рейку (рис. 53).
Какой
из ответов соответствует модулю ускорения
рейки
в момент времени
![]() ?
Радиусы колес:
,
(
- в
,
- в
).
?
Радиусы колес:
,
(
- в
,
- в
).
 А.
. B.
.
А.
. B.
.
C.
. D.
![]() .
.
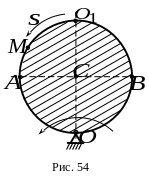
4. По ободу диска радиусом (рис.54) от точки движется точка по закону ( - в , - в ) Одновременно диск вращается против хода часовой стрелки вокруг неподвижной оси в плоскости чертежа по закону ( - в , - в ).
Какой из ответов соответствует модулю абсолютной скорости точки в момент времени , если , а точка находится в положении ?
А.
![]() . B.
. B.
![]() .
.
C.
. D.
![]() .
.
5.
Равносторонний треугольник со стороной
![]() движется в плоскости чертежа
движется в плоскости чертежа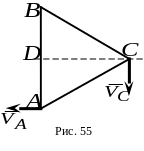 так, что в данный момент времени скорость
точки
равна
;
,
а вектор скорости точки
:
(рис. 55).
так, что в данный момент времени скорость
точки
равна
;
,
а вектор скорости точки
:
(рис. 55).
Какой из ответов соответствует модулю скорости точки ?
А. .
B. .
C.
![]() .
.
D.
![]() .
.
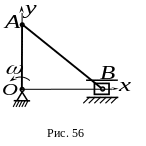
6.
В кривошипно-ползунном механизме
кривошип
вращается равномерно вокруг неподвижной
оси
,
перпендикулярной плоскости чертежа, с
угловой скоростью
.
![]() ,
(рис.56).
,
(рис.56).
Определить модуль вращательного ускорения точки при ее вращении вокруг полюса в указанном на рисунке положении механизма.
А.
. B.
![]() .
.
C. . D. .
Тест №15
1.
Автомобиль массы
приводится в движение силой
,
постоянной по модулю и направлению.
Определить на каком пути
![]() он достигнет скорости
.
При решении использовать дифференциальное
уравнение движения автомобиля, считая
его материальной точкой.
он достигнет скорости
.
При решении использовать дифференциальное
уравнение движения автомобиля, считая
его материальной точкой.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
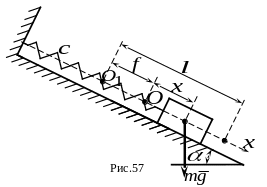
2.На
гладкой плоскости, наклоненной к
горизонту под углом
,
находится груз массы
,
прикрепленный к пружине с коэффициентом
жесткости
(рис. 57). Определить закон колебаний
груза, если в начальный момент времени
пружина была растянута из ненапряженного
(недеформированного) состояния на
величину
![]() и груз был отпущен без начальной скорости.
и груз был отпущен без начальной скорости.
На рисунке точка - положение груза при недеформированной пружине; точка - положение равновесия груза; - величина деформации пружины при равновесии груза. Текущее положение груза обозначено координатой .
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
3.
Маховик массы
приводится во вращательное движение
вокруг оси
постоянным вращающим моментом
.
С каким угловым ускорением
будет вращаться маховик, если его радиус
инерции относительно оси
равен
![]() ?
?
Применить дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
4.
Вал с моментом инерции
![]() ,
вращающийся с угловой скоростью
,
вращающийся с угловой скоростью
![]() вокруг оси
,
проходящей через центр масс вала, после
включения тормоза остановился, совершив
оборотов. Определить величину тормозного
момента
вокруг оси
,
проходящей через центр масс вала, после
включения тормоза остановился, совершив
оборотов. Определить величину тормозного
момента
![]() ,
считая ее постоянной.
,
считая ее постоянной.
Применить теорему об изменении кинетической энергии системы.
А.
![]() .
.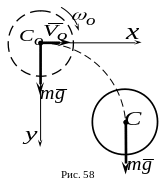
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
5.
Диск массы
падает в вертикальной плоскости под
действием силы тяжести (рис.58). В начальный
момент диску была сообщена угловая
скорость
,
а его центр масс
,
находившийся в начале координат, получил
горизонтально направленную скорость
![]() .
Угол поворота диска
образован осью
.
Угол поворота диска
образован осью
![]() и диаметром диска, занимавшим в начальный
момент горизонтальное положение. Силами
сопротивления пренебречь.
и диаметром диска, занимавшим в начальный
момент горизонтальное положение. Силами
сопротивления пренебречь.
Определить уравнения движения диска. Применить дифференциальные уравнения плоского движения твердого тела.
А.![]() B.
B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
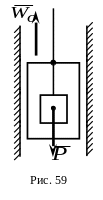
6.
Груз весом
(рис.59) подвешен с помощью невесомой
нерастяжимой нити к потолку кабины
лифта, поднимающегося с постоянным
ускорением
![]() .
Нить выдерживает усилие, не превосходящее
.
Нить выдерживает усилие, не превосходящее
![]() .
Определить наибольшее значение ускорения
.
.
Определить наибольшее значение ускорения
.
Применить метод кинетостатики.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
7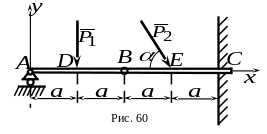 .
Составная балка
.
Составная балка
![]() находится в равновесии и испытывает
действие двух активных сил
находится в равновесии и испытывает
действие двух активных сил
![]() и
и
![]() ,
причем вектор силы
наклонен к горизонту под углом
(рис. 60). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль реакции левой шарнирной
опоры
.
Длины участков балок заданы отрезками
длиной
каждый.
,
причем вектор силы
наклонен к горизонту под углом
(рис. 60). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль реакции левой шарнирной
опоры
.
Длины участков балок заданы отрезками
длиной
каждый.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
8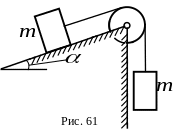 .
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы одинаковой массы
(рис.61). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
.
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы одинаковой массы
(рис.61). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
Использовать уравнение Лагранжа второго рода.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
Тест №16
1. Автомобиль массы приводится в движение силой , постоянной по модулю и направлению. Определить какой скорости он достигнет на пути . При решении использовать дифференциальное уравнение движения автомобиля, считая его материальной точкой.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
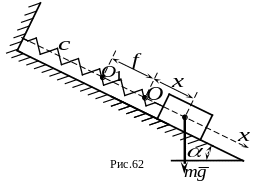
2.На
гладкой плоскости, наклоненной к
горизонту под углом
,
находится груз массы
,
прикрепленный к пружине с коэффициентом
жесткости
(рис. 62). Определить закон колебаний
груза, если в начальный момент времени
пружина была растянута на величину
и грузу была сообщена начальная скорость
![]() ,
направленная вниз.
,
направленная вниз.
На рисунке точка - положение груза при недеформированной пружине; точка - положение равновесия груза; текущее положение груза обозначено координатой .
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
3. Маховик массы приводится во вращательное движение вокруг оси постоянным вращающим моментом . Определить угловую скорость вращения маховика в момент времени , если его радиус инерции относительно оси равен .
Применить дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
4. Вал с моментом инерции , вращающийся с угловой скоростью вокруг оси , проходящей через центр масс вала, после включения тормоза остановился под действием тормозного момента . Определить число оборотов вала до остановки, считая тормозной момент постоянным.
Применить теорему об изменении кинетической энергии системы.
А.
![]() .
.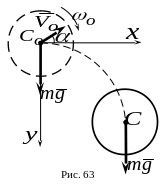
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
5. Диск массы падает в вертикальной плоскости под действием силы тяжести (рис.63). В начальный момент диску была сообщена угловая скорость , а его центр масс , находившийся в начале координат, получил скорость , направленную под углом к оси . Угол поворота диска образован осью и диаметром диска, занимавшим в начальный момент горизонтальное положение. Силами сопротивления пренебречь.
Определить уравнения движения диска. Применить дифференциальные уравнения плоского движения твердого тела.
А.![]() B.
B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
6.
Груз весом
(рис.64) подвешен с помощью невесомой
нерастяжимой нити к потолку кабины
лифта, поднимающегося с постоянным
ускорением
.
Нить выдерживает усилие, не превосходящее
![]() .
Определить наибольшее значение ускорения
.
.
Определить наибольшее значение ускорения
.
Применить
метод кинетостатики.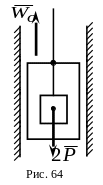
А. .
B. .
C.
![]() .
.
D. .
7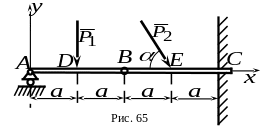 .
Составная балка
(рис. 65) находится в равновесии и испытывает
действие двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
.
Применяя принцип освобождаемости от
связей и принцип возможных перемещений,
определить модуль момента в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
.
Составная балка
(рис. 65) находится в равновесии и испытывает
действие двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
.
Применяя принцип освобождаемости от
связей и принцип возможных перемещений,
определить модуль момента в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
8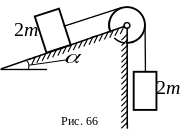 .
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы одинаковой массы
.
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы одинаковой массы
![]() (рис.66). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов. Использовать
уравнение Лагранжа второго рода.
(рис.66). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов. Использовать
уравнение Лагранжа второго рода.
А. . B. .
C. . D. .
Тест №17
1. Автомобиль массы приводится в движение силой , постоянной по модулю и направлению. Определить за какое время автомобиль пройдет путь . При решении использовать дифференциальное уравнение движения автомобиля, считая его материальной точкой.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
2.На
гладкой плоскости, наклоненной к
горизонту под углом
,
находится груз массы
,
прикрепленный к пружине с коэффициентом
жесткости
(рис. 67). Определить закон колебаний
груза, если в начальный момент времени
пружина была растянута на величину
![]() ,
а груз был отпущен без начальной скорости.
,
а груз был отпущен без начальной скорости.
Н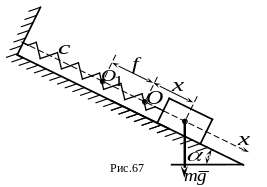 а
рисунке точка
- положение груза при недеформированной
пружине; точка
- положение равновесия груза;
- величина деформации пружины при
равновесии груза. Текущее положение
груза обозначено координатой
.
а
рисунке точка
- положение груза при недеформированной
пружине; точка
- положение равновесия груза;
- величина деформации пружины при
равновесии груза. Текущее положение
груза обозначено координатой
.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
3. Маховик массы приводится во вращательное движение вокруг оси постоянным вращающим моментом . Определить, на какой угол поворота повернется маховик за время , если его радиус инерции относительно оси равен .
Применить дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
4. Вал массы , вращающийся с угловой скоростью вокруг оси , проходящей через центр масс вала, после включения тормоза остановился, совершив оборотов. Определить величину тормозного момента , считая ее постоянной, если радиус инерции вала относительно оси равен .
Применить теорему об изменении кинетической энергии системы.
А.
![]() .
.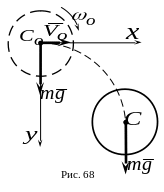
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
5. Диск массы падает в вертикальной плоскости под действием силы тяжести (рис.68). В начальный момент диску была сообщена угловая скорость , а его центр масс , находившийся в начале координат, получил горизонтально направленную скорость .
Определить
уравнение
![]() скорости центра масс диска
.
Применить дифференциальные уравнения
плоского движения твердого тела.
скорости центра масс диска
.
Применить дифференциальные уравнения
плоского движения твердого тела.
А.
![]() B.
B.
![]() .
.
C.
![]() D.
D.
![]() .
.
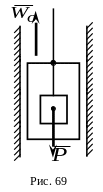
6. Груз весом (рис.69) подвешен с помощью невесомой нерастяжимой нити к потолку кабины лифта, поднимающегося с постоянным ускорением . Нить выдерживает усилие, не превосходящее . Определить наибольшее значение ускорения .
Применить метод кинетостатики.
А. . B. .
C. . D. .
7 .
Составная балка
находится в равновесии и испытывает
действие двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
(рис. 70). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль вертикальной
составляющей
.
Составная балка
находится в равновесии и испытывает
действие двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
(рис. 70). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль вертикальной
составляющей
![]() реакции
в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
реакции
в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
8.
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы одинаковой массы
![]() (рис.71). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
(рис.71). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
Использовать уравнение Лагранжа второго рода.
А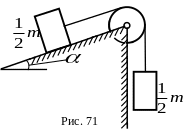 .
.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
Тест №18
1. Автомобиль массы приводится в движение силой , постоянной по модулю и направлению. Определить, какой путь пройдет автомобиль за время . При решении использовать дифференциальное уравнение движения автомобиля, считая его материальной точкой.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
2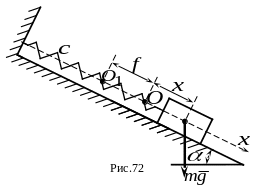 .На
гладкой плоскости, наклоненной к
горизонту под углом
,
находится груз массы
,
прикрепленный к пружине с коэффициентом
жесткости
(рис. 72). Определить закон колебаний
груза, если в начальный момент времени
пружина была растянута на величину
и грузу была скорость
,
направленная вверх.
.На
гладкой плоскости, наклоненной к
горизонту под углом
,
находится груз массы
,
прикрепленный к пружине с коэффициентом
жесткости
(рис. 72). Определить закон колебаний
груза, если в начальный момент времени
пружина была растянута на величину
и грузу была скорость
,
направленная вверх.
На рисунке точка - положение груза при недеформированной пружине; точка - положение равновесия груза. Текущее положение груза обозначено координатой .
А. . B. .
C.
![]() . D.
.
. D.
.
3. Маховик массы приводится во вращательное движение из состояния покоя вокруг оси постоянным вращающим моментом . Определить, на какой угол поворота повернется маховик при достижении угловой скорости , если его радиус инерции относительно оси равен .
Применить дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
4. Вал массы , вращающийся с угловой скоростью вокруг оси , проходящей через центр масс вала, после включения тормоза остановился под действием постоянного по величине тормозного момента . Определить число оборотов вала до остановки, если радиус инерции вала относительно оси равен .
Применить теорему об изменении кинетической энергии системы.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
5.
Диск массы
падает в вертикальной плоскости под
действием силы тяжести (рис.73). В начальный
момент диску была сообщена угловая
скорость
,
а его центр масс
,
находившийся в начале координат, получил
горизонтально направленную скорость
.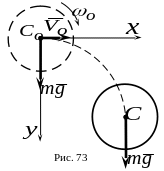
Определить угловую скорость вращения диска. Применить дифференциальные уравнения плоского движения твердого тела.
А.
![]() B.
B.
![]() .
.
C.
![]() .
D.
.
D.
![]() .
.
6.
Груз весом
(рис.74) подвешен с помощью невесомой
нерастяжимой нити к потолку кабины
лифта, поднимающегося с постоянным
ускорением
.
Нить выдерживает усилие, не превосходящее
![]() .
Опр
.
Опр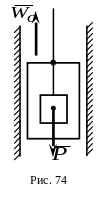 еделить
наибольшее значение ускорения
.
еделить
наибольшее значение ускорения
.
Применить метод кинетостатики.
А. .
B. .
C.
![]() .
.
D. .
7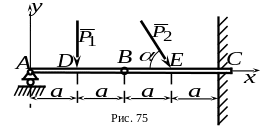 .
Составная балка
находится в равновесии и испытывает
действие двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
(рис. 75). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль горизонтальной
составляющей
.
Составная балка
находится в равновесии и испытывает
действие двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
(рис. 75). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль горизонтальной
составляющей
![]() реакции в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
реакции в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
8. Через невесомый блок переброшен невесомый нерастяжимый трос, к концам которого прикреплены грузы массами и (рис.76). Пренебрегая трением на оси блока и на наклонной плоскости, а также проскальзыванием троса по блоку, определить ускорения грузов.
И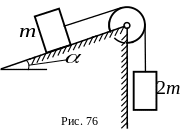 спользовать
уравнение Лагранжа второго рода.
спользовать
уравнение Лагранжа второго рода.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D. .
Тест №19
1. Автомобиль массы приводится в движение из состояния покоя силой , постоянной по модулю и направлению. Определить на каком пути он достигнет скорости . При решении использовать дифференциальное уравнение движения автомобиля, считая его материальной точкой.
А.
![]() . B.
.
. B.
.
C. . D. .
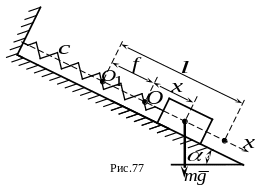
2.На гладкой плоскости, наклоненной к горизонту под углом , находится груз массы , прикрепленный к пружине с коэффициентом жесткости (рис. 77). Определить период свободных колебаний груза, предварительно доказав, что имеют место свободные колебания, если в начальный момент времени пружина была растянута из ненапряженного (недеформированного) состояния на величину , а груз был отпущен без начальной скорости.
На рисунке точка - положение груза при недеформированной пружине; точка - положение равновесия груза; - величина деформации пружины при равновесии груза. Текущее положение груза обозначено координатой .
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
3. Маховик массы приводится во вращательное движение вокруг оси из состояния покоя постоянным вращающим моментом . С каким угловым ускорением будет вращаться маховик, если его радиус инерции относительно оси равен ?
Применить дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
А.
![]() . B.
. B.
![]() .
.
C.
. D.
![]() .
.
4. Вал массы , вращающийся с угловой скоростью вокруг оси , проходящей через центр масс вала, после включения тормоза остановился, совершив оборотов. Определить величину тормозного момента , считая ее постоянной, если радиус инерции вала относительно оси равен .
Применить теорему об изменении кинетической энергии системы.
А.
. B.
![]() .
.
C.
![]() . D.
.
. D.
.
5.
Диск массы
падает в вертикальн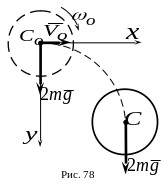 ой
плоскости под действием силы тяжести
(рис.78). В начальный момент диску была
сообщена угловая скорость
,
а его центр масс
,
находившийся в начале координат, получил
горизонтально направленную скорость
.
Угол поворота диска
образован осью
и диаметром диска, занимавшим в начальный
момент горизонтальное положение. Силами
сопротивления пренебречь.
ой
плоскости под действием силы тяжести
(рис.78). В начальный момент диску была
сообщена угловая скорость
,
а его центр масс
,
находившийся в начале координат, получил
горизонтально направленную скорость
.
Угол поворота диска
образован осью
и диаметром диска, занимавшим в начальный
момент горизонтальное положение. Силами
сопротивления пренебречь.
Определить уравнения движения диска. Применить дифференциальные уравнения плоского движения твердого тела.
А.
B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
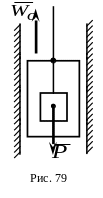
6.
Груз весом
(рис.79) подвешен с помощью невесомой
нерастяжимой нити к потолку кабины
лифта, поднимающегося с постоянным
ускорением
.
Нить выдерживает усилие, не превосходящее
![]() .
Определить наибольшее значение ускорения
.
.
Определить наибольшее значение ускорения
.
Применить метод кинетостатики.
А.
![]() .
.
B. .
C.
![]() .
.
D. .
7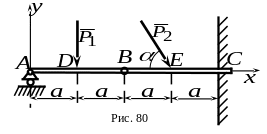 .
Составная балка
(рис. 80) находится в равновесии под
действием двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
.
Применяя принцип освобождаемости от
связей и принцип возможных перемещений,
определить модуль вертикальной реакции
в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
.
Составная балка
(рис. 80) находится в равновесии под
действием двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
.
Применяя принцип освобождаемости от
связей и принцип возможных перемещений,
определить модуль вертикальной реакции
в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
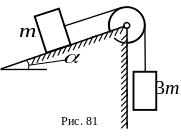
8.
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы с массами
![]() и
(рис.81). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
и
(рис.81). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
Использовать уравнение Лагранжа второго рода.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
Тест №20
1. Автомобиль массы приводится в движение силой , постоянной по модулю и направлению. Определить, какой скорости достигнет автомобиль на пути . При решении использовать дифференциальное уравнение движения автомобиля, считая его материальной точкой.
А. . B. .
C.
![]() . D.
. D.
![]() .
.
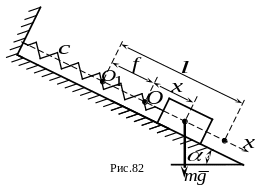
2.На гладкой плоскости, наклоненной к горизонту под углом , находится груз массы , прикрепленный к пружине с коэффициентом жесткости (рис. 82). Определить амплитуду свободных колебаний груза, доказав предварительно, что груз совершает именно свободные колебания, если в начальный момент времени пружина была растянута из ненапряженного (недеформированного) состояния на величину , а груз был отпущен без начальной скорости.
На рисунке точка - положение груза при недеформированной пружине; точка - положение равновесия груза; - величина деформации пружины при равновесии груза. Текущее положение груза обозначено координатой .
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
3. Маховик массы приводится во вращательное движение вокруг оси постоянным вращающим моментом . Определить угловую скорость вращения маховика в момент времени , если его радиус инерции относительно оси равен .
Применить дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
А. . B. .
C. . D. .
4. Вал массы , вращающийся с угловой скоростью вокруг оси , проходящей через центр масс вала, после включения тормоза остановился под действием постоянного по величине тормозного момента . Определить число оборотов вала до остановки, если радиус инерции вала относительно оси равен .
Применить теорему об изменении кинетической энергии системы.
А.
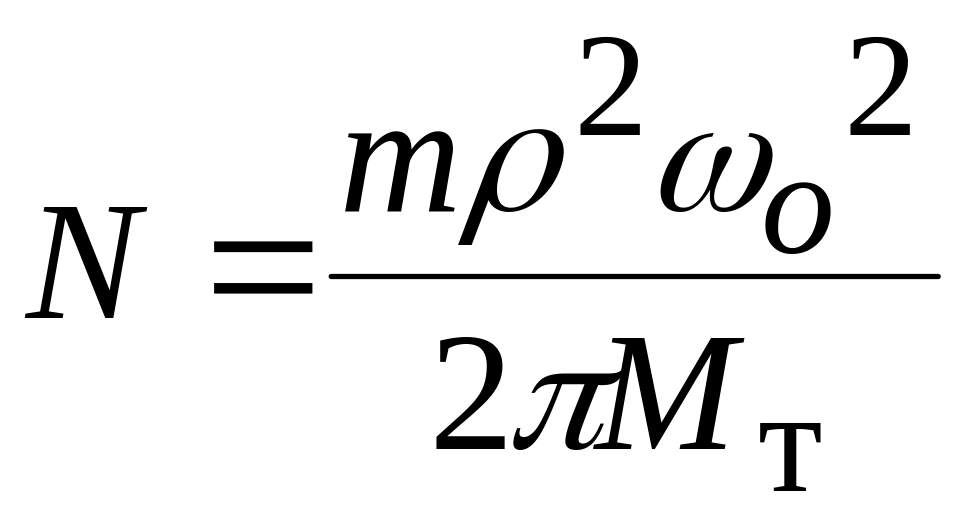 . B.
. B.
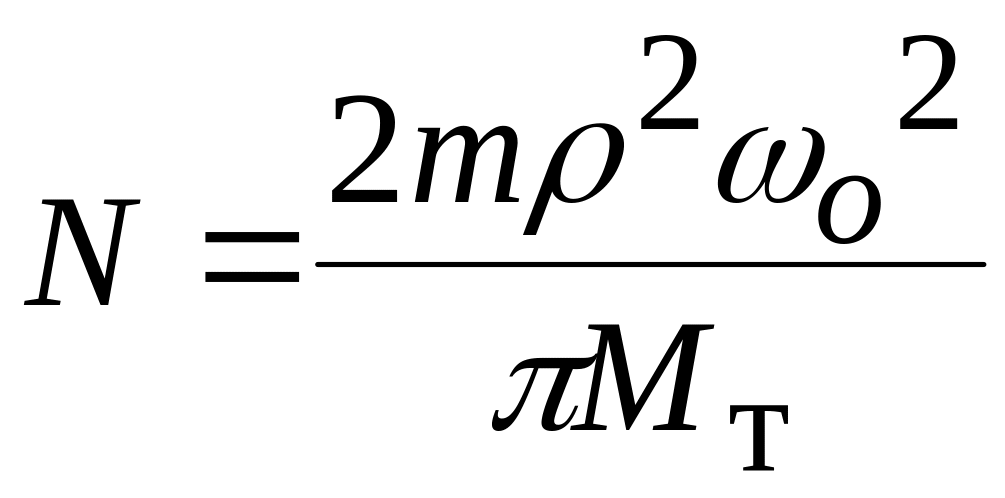 .
.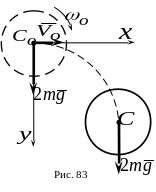
C.
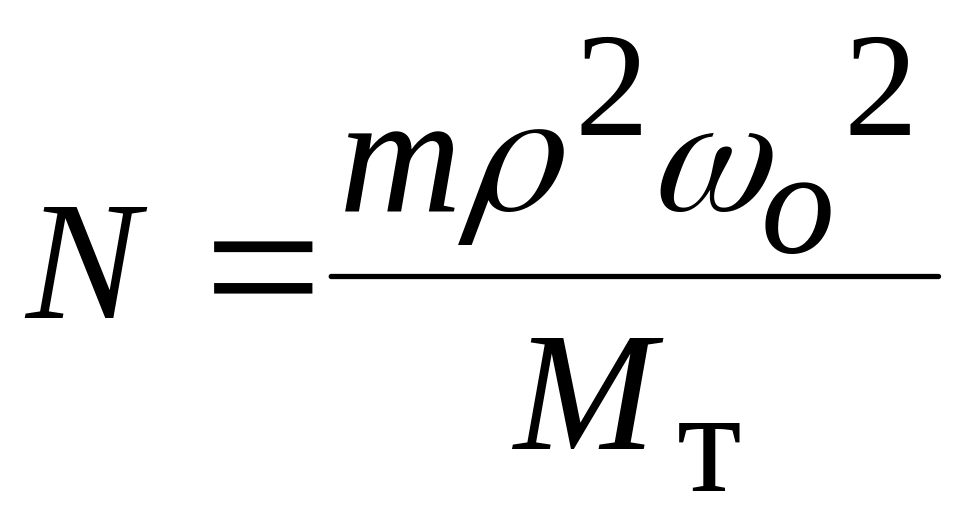 . D.
. D.
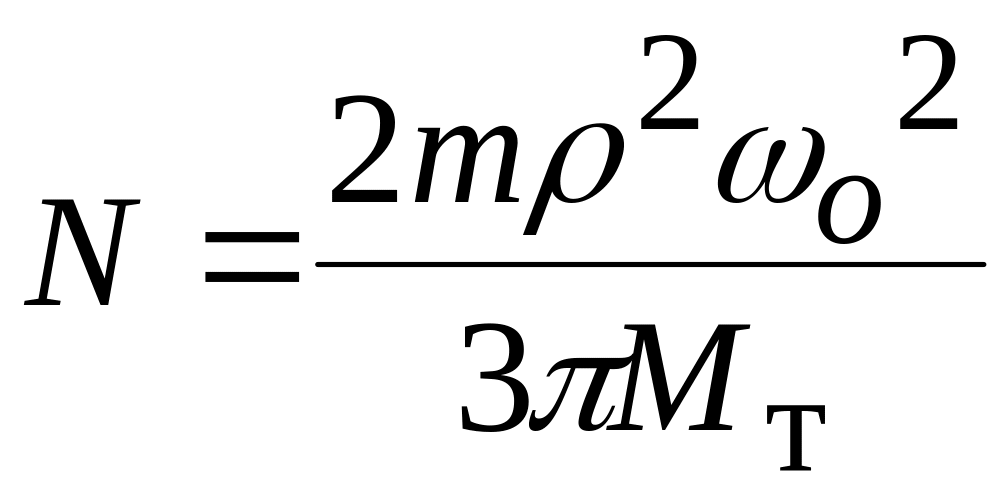 .
.
5. Диск массы падает в вертикальной плоскости под действием силы тяжести (рис.83). В начальный момент диску была сообщена угловая скорость , а его центр масс , находившийся в начале координат, получил горизонтально направленную скорость . Силами сопротивления пренебречь.
Определить уравнение скорости центра масс диска .
Применить дифференциальные уравнения плоского движения твердого тела.
А.
![]() B.
.
B.
.
C. D. .
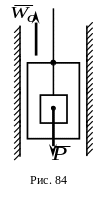
6. Груз весом (рис.84) подвешен с помощью невесомой нерастяжимой нити к потолку кабины лифта, поднимающегося с постоянным ускорением . Нить выдерживает усилие, не превосходящее . Определить наибольшее значение ускорения .
Применить метод кинетостатики.
А. .
B. .
C. .
D. .
7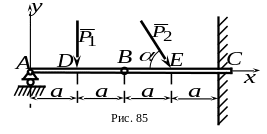 .
Составная балка
находится в равновесии под действием
двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
(рис. 85). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль вертикальной
составляющей реакции
в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
.
Составная балка
находится в равновесии под действием
двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
(рис. 85). Применяя принцип освобождаемости
от связей и принцип возможных перемещений,
определить модуль вертикальной
составляющей реакции
в заделке
.
Длины участков балок заданы отрезками
длиной
каждый.
А. . B. .
C. . D. .
8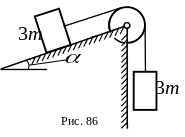 .
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы одинаковой массы
(рис.86). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
.
Через невесомый блок переброшен невесомый
нерастяжимый трос, к концам которого
прикреплены грузы одинаковой массы
(рис.86). Пренебрегая трением на оси блока
и на наклонной плоскости, а также
проскальзыванием троса по блоку,
определить ускорения грузов.
Использовать уравнение Лагранжа второго рода.
А. . B. .
C. . D. .
Тест №21
1. Автомобиль массы приводится в движение из состояния покоя силой , постоянной по модулю и направлению. Определить, за какое время автомобиль пройдет путь . При решении использовать дифференциальное уравнение движения автомобиля, считая его материальной точкой.
А. . B. .
C.
![]() . D.
. D.
![]() .
.
2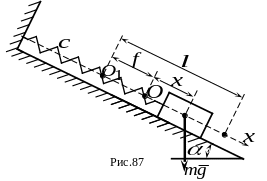 .На
гладкой плоскости, наклоненной к
горизонту под углом
,
находится груз массы
,
прикрепленный к пружине с коэффициентом
жесткости
(рис. 87). Определить амплитуду свободных
колебаний груза, доказав предварительно,
что груз совершает именно свободные
колебания, если в начальный момент
времени пружина была растянута из
ненапряженного (недеформированного)
состояния на величину
,
а грузу была сообщена начальная скорость
,
направленная вниз.
.На
гладкой плоскости, наклоненной к
горизонту под углом
,
находится груз массы
,
прикрепленный к пружине с коэффициентом
жесткости
(рис. 87). Определить амплитуду свободных
колебаний груза, доказав предварительно,
что груз совершает именно свободные
колебания, если в начальный момент
времени пружина была растянута из
ненапряженного (недеформированного)
состояния на величину
,
а грузу была сообщена начальная скорость
,
направленная вниз.
На рисунке точка - положение груза при недеформированной пружине; точка - положение равновесия груза; - величина деформации пружины при равновесии груза. Текущее положение груза обозначено координатой .
А.
![]() . B.
. B.
![]() .
.
C.
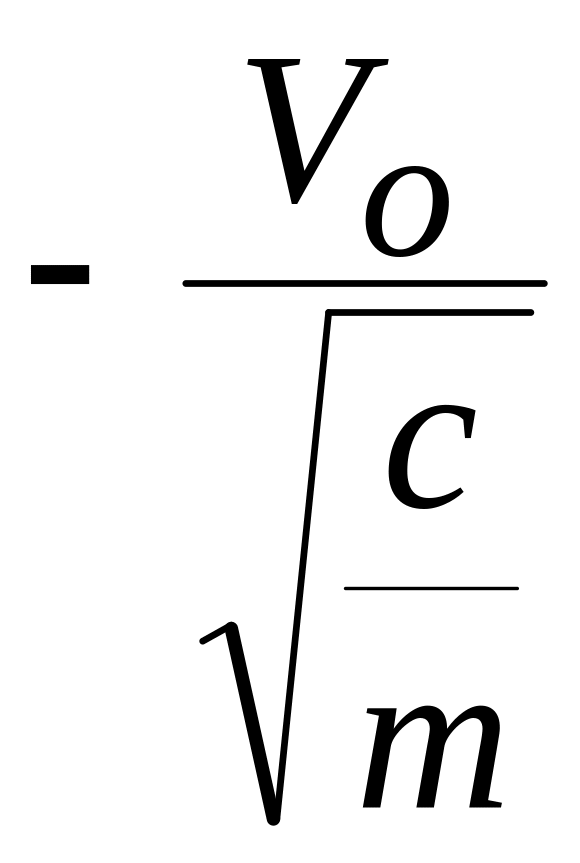 . D.
. D.
![]() .
.
3. Маховик массы приводится во вращательное движение вокруг оси постоянным вращающим моментом . Определить, на какой угол поворота повернется маховик за время , если его радиус инерции относительно оси равен .
Применить дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.
А.
. B.
![]() .
.
C. . D. .
4. Вал с моментом инерции приводится во вращение вокруг оси постоянным по модулю вращающим моментом . Определить угловую скорость вращения вала вокруг оси , проходящей через центр масс вала, когда он совершит число оборотов, равное .
Применить теорему об изменении кинетической энергии системы.
А.
![]() . B.
. B.
![]() .
.
C.
![]() . D.
. D.
![]() .
.
5.
Диск массы
падает в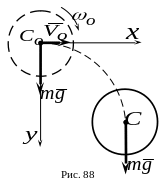 вертикальной плоскости под действием
силы тяжести (рис.88). В начальный момент
диску была сообщена угловая скорость
,
а его центр масс
,
находившийся в начале координат, получил
горизонтально направленную скорость
.
Угол поворота диска
образован осью
и диаметром диска, занимавшим в начальный
момент горизонтальное положение. Силами
сопротивления пренебречь.
вертикальной плоскости под действием
силы тяжести (рис.88). В начальный момент
диску была сообщена угловая скорость
,
а его центр масс
,
находившийся в начале координат, получил
горизонтально направленную скорость
.
Угол поворота диска
образован осью
и диаметром диска, занимавшим в начальный
момент горизонтальное положение. Силами
сопротивления пренебречь.
Определить
уравнения угловой скорости диска
![]() .
Применить дифференциальные уравнения
плоского движения твердого тела.
.
Применить дифференциальные уравнения
плоского движения твердого тела.
А. B. .
C. . D. .
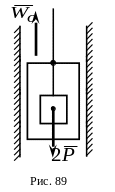 6.
Груз весом
(рис.89) подвешен с помощью невесомой
нерастяжимой нити к потолку кабины
лифта, поднимающегося с постоянным
ускорением
.
Нить выдерживает усилие, не превосходящее
6.
Груз весом
(рис.89) подвешен с помощью невесомой
нерастяжимой нити к потолку кабины
лифта, поднимающегося с постоянным
ускорением
.
Нить выдерживает усилие, не превосходящее
![]() .
Определить наибольшее значение ускорения
.
.
Определить наибольшее значение ускорения
.
Применить метод кинетостатики.
А. . B. .
C.
![]() . D.
.
. D.
.
7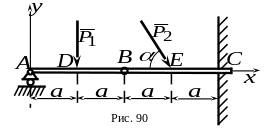 .
Составная балка
(рис. 90) находится в равновесии под
действием двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
.
Применяя принцип освобождаемости от
связей и принцип возможных перемещений,
определить модуль реакции левой шарнирной
опоры
.
Длины участков балок заданы отрезками
длиной
каждый.
.
Составная балка
(рис. 90) находится в равновесии под
действием двух активных сил
и
,
причем вектор силы
наклонен к горизонту под углом
.
Применяя принцип освобождаемости от
связей и принцип возможных перемещений,
определить модуль реакции левой шарнирной
опоры
.
Длины участков балок заданы отрезками
длиной
каждый.
А.
![]() . B.
.
. B.
.
C. . D. .
8. Через невесомый блок переброшен невесомый нерастяжимый трос, к концам которого прикреплены грузы массами и (рис.91). Пренебрегая трением на оси блока и на наклонной плоскости, а также проскальзыванием троса по блоку, определить ускорения грузов.
И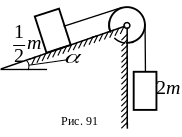 спользовать
уравнение Лагранжа второго рода.
спользовать
уравнение Лагранжа второго рода.
А.
![]() .
.
B.
![]() .
.
C.
![]() .
.
D.
![]() .
.
Таблица правильных ответов на тесты текущего контроля
№ тестов |
Номера вопросов/Номера правильных ответов |
||||||||
1 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
2 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
3 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
4 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
5 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
6 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
7 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
8 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
9 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
10 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
11 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
12 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
13 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
14 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
15 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
16 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
17 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
18 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
19 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
20 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
21 |
Номер вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Ответ |
|
|
|
|
|
|
|
|
|
