2.1.1. Кинематические способы задания движения точки

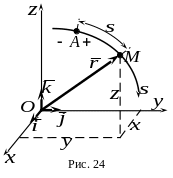
Основной задачей кинематики точки является определение кинематических характеристик ее движения: траектории, т. е. линии, описываемой точкой в пространстве, скорости и ускорения. Но для этого необходимо задать движение точки, то есть уметь определять ее положение относительно выбранной системы отсчета в любой момент времени. Существуют три способа задания движения точки: векторный, координатный и естественный.

Векторный способ. Пусть точка (рис. 24) движется относительно некоторой системы отсчета , условно принимаемой за неподвижную. Положение точки можно задать ее радиус-вектором , проведенным из начала координат . При движении точки радиус-вектор в общем случае изменяется по модулю и направлению, т. е. является вектор-функцией времени.

. (36)

Уравнение (36) позволяет в любой момент времени определить радиус-вектор (а значит положение точки ) и называется уравнением (или законом) движения точки в векторной форме. Траектория точки является геометрическим местом концов радиус-вектора , т. е. представляет собой годограф этого вектора.

Координатный способ. Положение точки в выбранной системе отсчета можно задать тремя ее координатами (рис. 24).

При движении точки ее координаты – непрерывные функции времени:

. (37)

Если точка движется в одной плоскости, например в плоскости , то будем иметь два уравнения движения:

. (38)

Прямолинейное движение точки определяется одним уравнением

. (39)

Уравнения (37), (38), (39) одновременно являются параметрическими уравнениями траектории (параметр – время ). Чтобы получить ее в виде зависимости между координатами, нужно исключить из уравнений движения (37)-(39) параметр .

Уравнения (37), (38), (39) вполне определяют положение точки в любой момент и поэтому называются уравнениями движения точки в декартовых координатах. Эти функции, отражающие реальный физический процесс, должны быть непрерывными, однозначными и дважды дифференцируемыми по времени.

Естественный способ. Этот способ применим в тех случаях, когда траектория точки заранее известна. Траектория рассматривается как криволинейная координатная ось. Положение точки на траектории определяется дуговой (криволинейной) координатой , отсчитываемой от некоторой неподвижной точки , выбранной за начало отсчета (рис.24).

Положительное и отрицательное направления отсчета координаты устанавливаются как на обычной, т. е. прямолинейной, координатной оси. При движении точки ее дуговая координата есть функция времени.

. (40)

Это уравнение называется законом движения точки по траектории. Не следует отождествлять дуговую координату с путем, пройденным точкой по траектории, который всегда является положительной величиной.

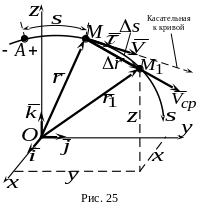
2.1.2. Скорость точки

Скорость точки – векторная величина, характеризующая быстроту и направление движения точки в данный момент времени.

Пусть движение точки относительно неподвижной системы отсчета задано уравнением , т. е. векторным способом. В момент времени точка занимает положение , определяемое радиус-вектором , а в момент – положение , определяемое радиус-вектором . Вектор , соединяющий положения и и равный приращению радиус-вектора за время называется вектором перемещения точки за время - . Векторная величина называется средней скоростью точки за время . Поскольку – положительная скалярная величина, то вектор направлен по хорде в сторону движения точки (рис. 25).

Скоростью точки в данный момент времени называется векторная величина , равная пределу, к которому стремится при :

(41)

(В механике производная от функции по времени может обозначаться точкой над функцией).

При положение точки неограниченно приближается к положению , а линия действия стремится к положению касательной к траектории в точке (рис.25).

Итак, вектор скорости точки в данный момент времени равен первой производной от радиус-вектора точки по времени и направлен по касательной к траектории в сторону ее движения.

Из рис. 24, 25 видно, что проекции радиус-вектора на координатные оси равны соответствующим координатам точки, а именно:

.

Поэтому согласно формуле разложения вектора по координатным осям имеем

, (42)

где – орты осей системы отсчета. Зависимость (42) устанавливает связь между векторным и координатным способами задания движения точки.

Пусть движение точки задано уравнениями (37). Согласно формулам (41) и (42) имеем

. (42а)

Так как система отсчета принята за неподвижную, орты ее осей постоянны по модулю и направлению и поэтому:

. (42б)

С учетом этого обстоятельства можно написать:

. (43)

С другой стороны, согласно формуле разложения вектора по координатным осям:

, (44)

где – проекции вектора скорости по координатным осям.

Сравнивая выражения (43) и (44), находим

. (45)

Проекции скорости точки на неподвижные оси декартовых координат равны первым производным по времени от соответствующих координат точки.

Модуль вектора скорости точки равен

. (46)

Направление вектора скорости находится по направляющим косинусам:

. (47)

Пусть заданы траектория точки и закон движения точки по траектории . Представим формулу (41) в виде

. (48)

Определим модуль и направление вектора . По определению производной вектора по скаляру :

,

где приращение радиус-вектора за время , – приращение дуговой координаты за то же время (рис.25).

Предел отношения длины хорды к длине стягиваемой ею дуги при равен единице. Поэтому

. (48а)

Вектор направлен по касательной к траектории точки, т. е. к годографу вектора в сторону положительного отсчета координаты .

Направление вектора не зависит от направления движения точки по траектории. Действительно, если точка движется в сторону положительного отсчета координаты , то и согласно формуле (47) направление вектора совпадает с направлением скорости точки . При движении в обратную сторону и направление векторов и противоположны.

Итак, вектор представляет собой единичный вектор (орт), направленный по оси касательной (рис. 25) в сторону положительного отсчета дуговой координаты . Обозначим его через . Тогда (48) примет вид

. (49)

Но с другой стороны (50),

где - проекция вектора на касательную ось. Сравнивая (49) и (50), находим

. (51)

Таким образом, проекция вектора скорости на ось касательной к траектории равна первой производной по времени от дуговой координаты.

Модуль вектора скорости можно представить в виде,

. (52)