1.3. Произвольная система сил
1.3.1. Приведение силы к данному центру
Р
ассмотрим
свободное твердое тело, на которое
воздействует сила
,
приложенная в точке
(рис.16). Выберем на линии действия силы
точку
и приложим к ней простейшую уравновешенную
систему сил
и
;
при этом силы
и
по модулю равны силе
и направлены по прямой
.
Кинематическое состояние тела при этом
не изменится, поскольку в точке
к телу приложена система сил, эквивалентная
нулю.
Рассматривая теперь силы и , можно их считать уравновешенной системой сил, приложенных в точках и ; на тело же будет действовать одна сила , равная силе по модулю и направленная вдоль той же прямой и в ту же сторону, но приложенная уже в точке .
О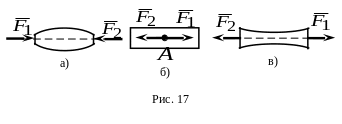
тсюда
следует, что силу, приложенную к твердому
телу, можно рассматривать как скользящий
вектор,
определяемый модулем, направлением и
линией действия. Точку
приложения силы можно переносить вдоль
линии ее действия в пределах данного
твердого тела.
Это положение неприменимо к деформируемому (например, упругому) телу.
Например, если к упругому телу приложить силы и (рис.17а), то тело сжимается; если перенести эти силы по линии действия в точку тела, то оно не будет деформироваться (рис.17б), а при расположении сил, указанном на рис.17в, тело растягивается. Итак, перенос точек приложения сил в упругом (деформируемом) теле меняет характер напряжений и деформаций в теле.
Рассмотрим
теперь приведение одной силы к данному
центру, не
лежащему на линии действия этой силы.
Пусть к свободному твердому телу в точке
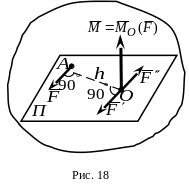приложена сила
(рис.18).
Возьмем
произвольную точку
(центр приведения) и проведем через нее
и силу
плоскость
.
Приложим в центре
уравновешенную систему сил
,
;
равных по модулю
и параллельных ей. Система сил
эквивалентна силе
.
С другой стороны, ее можно рассматривать
как состоящую из силы
,
геометрически равной силе
,
но приложенной в центре
,
и пары
,
называемой присоединенной.
Легко видеть, что момент присоединенной
пары
геометрически равен моменту силы
относительно центра
:
(смотри также рис.13).
Итак, сила, приложенная в какой-либо точке тела эквивалентна равной ей силе, приложенной в произвольно выбранном центре, и паре, момент которой равен моменту данной силы относительно этого центра.
1.3.2. Основная теорема статики
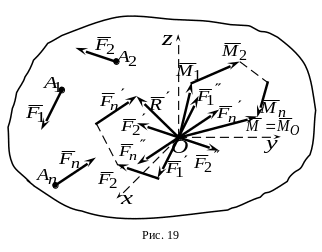
Пусть
на свободное твердое тело действует
система сил
,
расположенных как угодно в пространстве
и приложенных в точках
(рис.19). Выберем произвольно центр
и приведем все данные силы к этому центру
(центру
приведения).
В результате получим силы
,,равные
данным силам и приложенные в центре
и присоединенные пары
.
Моменты
этих присоединенных пар равны моментам
данных сил относительно центра приведения:
.
(25)
Складывая
силы
,
приложенные в центре
по правилу многоугольника, получаем
одну силу
.
Так как силы
равны данным силам
,
то можно записать
.
(26)
Вектор
,
равный геометрической сумме всех сил
системы, называется главным
вектором
системы сил.
Складывая
присоединенные пары
,
получим одну пару с моментом
,
равным геометрической сумме моментов
присоединенных пар.
.
(26а).
Учитывая (25), находим:
,
(26б).
или
,
где
.
(27).
Вектор
,
равный геометрической сумме моментов
всех сил системы относительно центра
приведения
,
называется главным
моментом
системы сил относительно этого центра.
Таким образом, доказана основная теорема статики: произвольную систему сил, приложенную к свободному твердому телу, можно привести к одной силе, равной главному вектору системы сил, и приложенной в центре приведения и к одной паре с моментом, равным главному моменту этой системы относительно центра приведения.
Не следует отождествлять главный вектор c равнодействующей, так как он заменяет систему сил в сочетании с главным моментом, в то время как равнодействующая , если она существует, одна заменяет систему сил.
При переносе центра приведения главный вектор не изменяется, а главный момент в общем случае изменяется.
Приведение произвольной системы сил к центру позволяет ответить на вопрос, являются ли две системы сил, приложенных к твердому телу, эквивалентными. Если при приведении этих двух систем к одному центру мы получим два равных главных вектора и главных момента, то можно утверждать, что такие две системы сил являются эквивалентными.
Случаи приведения произвольной системы сил к равнодействующей, к паре, к динаме изучаются студентами самостоятельно (см. [1],с. 94…97 или [2], с. 105…107).