1.2.4. Момент силы относительно оси

Введем сначала понятие проекции силы на плоскость. Пусть даны сила и некоторая плоскость . Опустим из начала и конца вектора силы перпендикуляры на эту плоскость (рис.12).

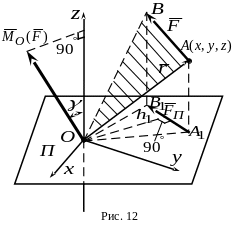Проекцией силы на плоскость называется вектор , начало и конец которого (точки ) совпадают с проекциями начала и конца силы (точки ).

Моментом силы относительно оси называется алгебраическая величина , равная произведению модуля проекции силы на плоскость , перпендикулярную к оси (т.е. совпадающую с плоскостью ), на кратчайшее расстояние от точки пересечения оси с плоскостью до линии действия проекции силы (рис.12).

Этому определению соответствует следующая зависимость.

. (18)

Момент силы относительно оси считается положительным, если смотря с положительного конца этой оси, видим, что сила стремится повернуть тело вокруг нее в направлении против хода часовой стрелки, и отрицательным, если - по ходу часовой стрелки.

Из определения следует, что момент силы относительно оси равен нулю в двух случаях:

1. Когда , т.е. сила параллельна оси ;

2. когда 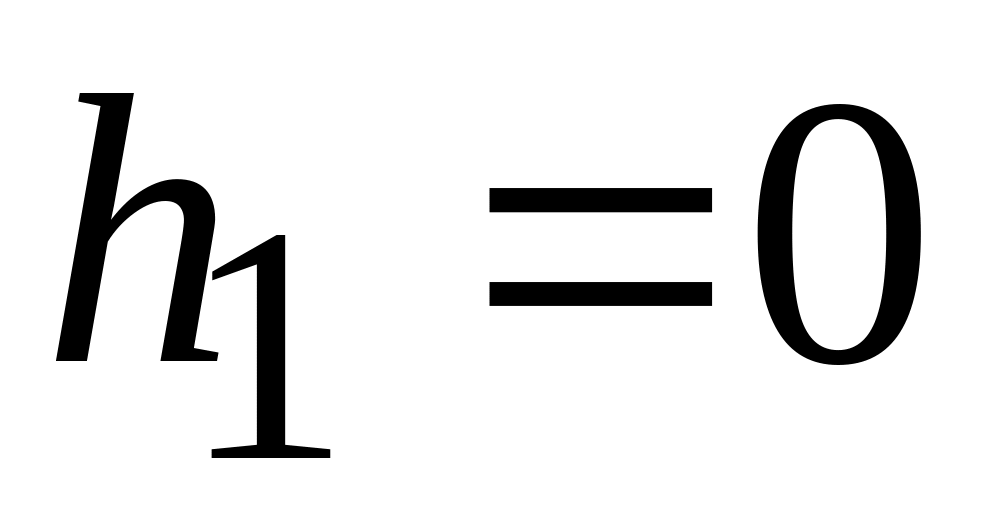, т.е. линия действия силы пересекает ось .

Объединяя эти два случая, можно сказать, что момент силы относительно оси равен нулю, если сила и ось располагаются в одной плоскости.

Момент силы относительно точки связан с моментом силы относительно оси. Эту связь можно выразить следующим образом:

Проекция момента силы относительно точки на ось, проходящую через эту точку, равна моменту силы относительно этой оси.

Пусть на тело действует сила , приложенная в точке . Выберем некоторую точку и проведем через нее ось произвольного направления. По определению момент силы относительно точки представляет собой вектор , перпендикулярный плоскости треугольника (рис.12). Его модуль равен

. (18а)

Спроектируем силу на плоскость , перпендикулярную оси . В ней располагаются оси и .

Момент силы относительно оси по определению равен

. (18б)

Треугольник является проекцией треугольника на плоскость . Следовательно

. (18в)

Здесь – угол между плоскостью треугольника и плоскостью , равный углу между вектором и осью , перпендикулярными этим плоскостям.

Умножая обе части последнего равенства на 2 и учитывая выражения для и , находим

. (18г)

Но , (18д)

т.е. равно проекции вектора на ось .

Поэтому окончательно имеем:

. (19)

Аналогично:

. (20)

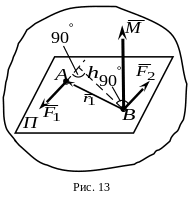Формулы (19) и (20) позволяют вместо формул (17) определять проекции вектора на координатные оси.

1.2.5. Пара сил и ее свойства

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на твердое тело (рис.13).

Плоскость , содержащая линии действия сил пары и называется плоскостью действия сил пары. Кратчайшее расстояние между линиями действия сил пары называется плечом пары.

Вращающее действие пары на твердое тело зависит от модуля сил пары , плеча , положения плоскости действия пары и направления вращения.

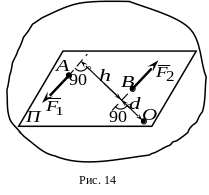Мерой этого действие пары является ее вектор-момент . Если все силы и пары, приложен ные к телу, лежат в одной плоскости, то момент пары можно рассматривать как алгебраическую величину, равную

. (21)

Момент пары считается положительным, если он стремиться вращать тело против хода часовой стрелки и отрицательным, если - по ходу часовой стрелки.

Момент пары, как и момент силы, измеряется в ( система СИ) и в (система МКГСС).

Алгебраическая сумма моментов сил пары относительно произвольной точки в плоскости ее действия не зависит от выбора этой точки и равна моменту пары. Действительно, определим сумму моментов сил и пары (рис.14) относительно произвольной точки , расположенной в плоскости действия пары.

,

где .

Так как , то получим:

. (21а)

Если силы и пары, приложенные к телу, лежат в разных плоскостях, то момент пары, как и момент силы, необходимо рассматривать как вектор. Вводим в связи с этим общее определение момента пары.

Моментом пары является вектор , равный по модулю произведению модуля сил пары на ее плечо и направленный перпендикулярно плоскости ее действия в ту сторону, откуда поворот, который пара стремится сообщить телу, виден происходящим в направлении против хода часовой стрелки (рис.13).

Модуль вектора равен

. (22)

Из определения векторов и следует, что момент пары (рис.13) равен по модулю и направлению моменту любой из сил пары (например, ) относительно точки приложения другой, то есть

.

Используя формулу 16, имеем:

. (23)

Таким образом, момент пары можно представить в виде векторного произведения (23), в котором – радиус-вектор точки приложения силы относительно точки приложения силы (рис.13).

Свойства пар выражаются следующими теоремами, которые приводятся здесь без доказательств.

1. Действие пары на твердое тело не изменится, если перенести пару в плоскости ее действия в любое другое положение.

2. Действие пары на твердое тело не изменится, если модуль сил пары и ее плечо изменить так, чтобы модуль момента пары сохранился неизменным.

3. Действие пары на твердое тело не изменится, если перенести пару в любую другую плоскость, параллельную плоскости ее действия.

4. Система пар, приложенных к твердому телу, может быть заменена одной результирующей парой с моментом , равным геометрической сумме моментов слагаемых пар:

. (24)

Из теорем следует, что пару, выраженную вектором , в твердом теле можно как угодно перенести в плоскости действия пары, а также перенести в любую параллельную плоскость; поэтому момент пары является свободным вектором, т.е. его можно изобразить приложенным в любой точке твердого тела.

Вопросы для самопроверки по теме 1.2

1. Определить момент силы относительно точки как алгебраическую величину, как вектор.

2. В каком случае момент силы относительно точки равен нулю?

3. Что называется моментом силы относительно оси?

4. В каких случаях момент силы относительно оси равен нулю?

5. Можно ли открыть дверь, если все приложенные к ней силы располагаются в плоскости двери?

6. Какова зависимость между моментами силы относительно оси и относительно точки, лежащей на этой оси?

7. Выведите формулы для моментов силы относительно трех координатных осей, используя представление о векторе момента силы относительно точки в виде векторного произведения.

8. Что называется парой сил? Чему равен момент пары?

9. Какие факторы определяют действие пары на твердое тело?

10. Как направлен, где приложен вектор момента пары?

11. Сформулируйте условие равновесия системы пар сил, приложенных к твердому телу.

12. Могут ли уравновесить друг друга две пары сил, лежащие в параллельных плоскостях; в пересекающихся плоскостях?

13. Каким образом можно изменять плечо и модуль сил пары, не изменяя действие пары на твердое тело?

14. Как складываются пары, лежащие в одной плоскости; в пересекающихся плоскостях?

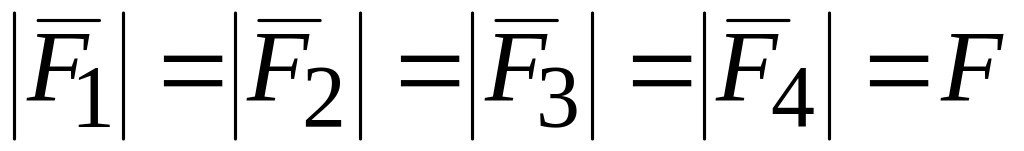15. Определите моменты сил относительно трех координатных осей (рис.15). Все силы приложены в точке куба со стороной и равны по модулю, т.е. . Оси координат направлены по граням куба.