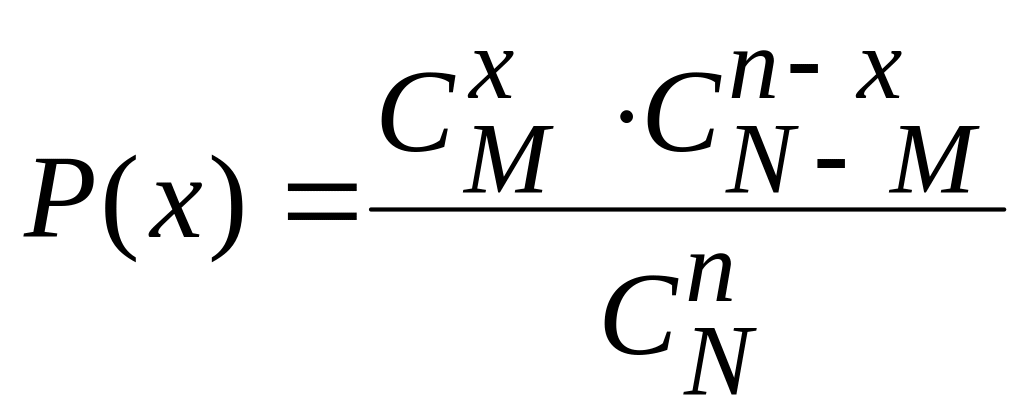2.1.5. Свойства математического ожидания и дисперсии

Свойства математического ожидания: 1. MC=C, где С=соnst,

2. M(CX)=CMX, 3. M(X+Y)=MX+MY,

4. M(XY)=MXMY (для независимых X и Y )

Свойства дисперсии: 1. DC=0 , где C=const, 2. D(CX)= C²DX,

3. D(XY)=DX+DY2cov(X,Y), где cov(X,Y)=M[(X-MX)(Y-MY)] – ковариация (математическое ожидание произведения отклонений случайных величин от их математических ожиданий), причем, для независимых X и Y cov(X,Y)=0.

4. D(XY)= DXDY + (MX)² DY + (MY)² DX =MX²MY²– (MX)²(MY)²– для независимых X и Y

Используя эти свойства, легко найти характеристики нормированной СВ . Тогда МZ=0, DZ=1, т.е. математическое ожидание нормированной СВ равно 0, а дисперсия равна 1. Действительно:

DZ = D[X-MX] = (DX+D[MX]) = 1, так как D[MX] = 0

2.1.6. Нормальное распределение

Наиболее распространённым видом распределения, часто использующимся на практике для непрерывной СВ Х, является нормальное распределение. Плотность нормального распределения: , где σ > 0, –∞ < a <∞. Если воспользоваться формулами для математического ожидания и дисперсии, то получим: МХ=а и Тот факт, что СВ Х характеризуется нормальным распределением (говорят также: подчинена нормальному закону) обозначают так: . В точках а±σ плотность f(x) имеет перегибы. С помощью замены это распределение приводится к стандартному виду с МХ=0 и DX=1 (рис.5, рис.6), для которого есть таблицы (см. приложение, табл.1П) значений f(z) и интегралов Лапласа F(z), Ф(z) или 2Ф(z):

;

Рис.5.

Рис.6.

При этом ; Ф(–z)= –Ф(z)

Функции (интегралы) Лапласа связаны соотношением F(z)=0,5+Ф(z)

Вероятность попадания случайной величины в интервал [b,c]:

Правило трех сигм заключается в предположении, что СВ X реально может принимать значения из интервала , так как вероятность

Сравним: ; .

Нормальное распределение широко используется при контроле качества продукции, экологических, экономических показателей, распознавании образов, технической и медицинской диагностике.

2.1.7. Другие виды распределений

Количество видов распределений случайной величины, используемых на практике, исчисляется десятками (хотя есть справочники, содержащие сотни видов распределений). Наиболее распространенные виды распределений для дискретной случайной величины приведены в табл.3. Здесь следует обратить внимание на то, что формулой Бернулли описывается биномиальное распределение, а не распределение Бернулли. Следует заметить также, что в схеме Бернулли число успехов в каждом отдельном испытании (0 или 1) имеет распределение Бернулли.

Таблица 3

Наименование распределения	Формула для вероятности P(x)	Матема-тическое ожидание	Дисперсия
1.Распределение Бернулли (аль-тернативной СВ)		MX=p	DX=p(1-p)
2. Биномиальное распределение	x=0,1,2,…,n	MX=np	DX=np(1-p)
3. Распределение Пуассона	х=0,1,2,…	MX=a	DX=a
4.Гипергеометри-ческое распределение	x=0,1,2,…,n
5.Геометрическое распределение	х=0,1,2,…

Различных видов распределений непрерывной случайной величины гораздо больше. Некоторые наиболее распространенные распределения сведены в таблицу 4. Кроме них широко используются также распределения Релея и Вейбулла, гамма-распределение и распределения, используемые в математической статистике. С некоторыми из них мы познакомимся позднее.

Таблица 4

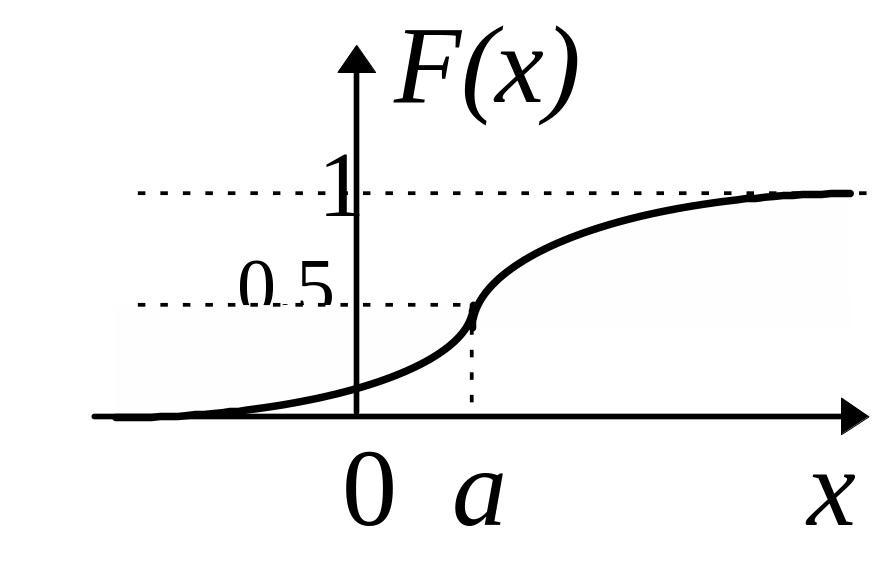
Наиме-нование	Формулы для функции распределения F(x) и плотности вероятности f(x)	Графики	Математическое ожидание и дисперсия
1.Равно-мерное
2.Нор-мальное
3.Экспо-ненциальное (показательное)	(λ>0)
4.Лога-рифми-чески нормальное
5.Бета- распределение	при и f(x)=0, гамма-функция	графики – на рис. 7

Рис.7