
- •4. Преобразование Фурье
- •4.1.Прямое дискретное преобразование Фурье
- •Подставив (6.2) в (6.1), получим
- •4.2. Обратное дискретное преобразование Фурье Обратное преобразование Фурье аналогового сигнала определяется соотношением
- •Рассмотрим отдельно четные и нечетные отсчеты спектра (отсюда и название алгоритма: прореживание по частоте).
4. Преобразование Фурье
Лекция №11
Введение
Жан Батист Жозеф Фурье (1768...1830), по-видимому, и не подозревал, какую роль будут иметь его ряды и преобразования в обработке телекоммуникационных сигналов. Фундаментальное понятие спектра сигнала связано с рядом и преобразованием Фурье. Исследование линейности телекоммуникационных систем сопровождается определением высших гармоник испытательного синусоидального сигнала по формулам Фурье. Анализ устройств обработки сигналов часто осуществляется с использованием разложения периодических функций в ряды Фурье.
Поэтому появление цифровой обработки сигналов потребовало разработки дискретного преобразования Фурье. В настоящее время дискретное преобразование Фурье используется не только как математический аппарат анализа и синтеза сигналов, но и для цифровой реализации устройств, например, анализаторов спектра, формирователей и демодуляторов сигналов с ортогональным частотным разделением, используемых в цифровом телевидении.
Данная тема включает следующие разделы:
4.1.Прямое дискретное преобразование Фурье,
4.2.Обратное дискретное преобразование Фурье,
4.3. Алгоритм быстрого преобразования Фурье с прореживанием во времени,
4.4. Алгоритм быстрого преобразования Фурье с прореживанием по частоте,
4.1.Прямое дискретное преобразование Фурье
На рисунке 4.1 показан дискретный сигнал xn , содержащий N отсчетов. Длительность сигнала Tc = TД N, где TД - интервал дискретизации. На этом же рисунке приведена последовательность (t) дельта - функций (t - n TД).
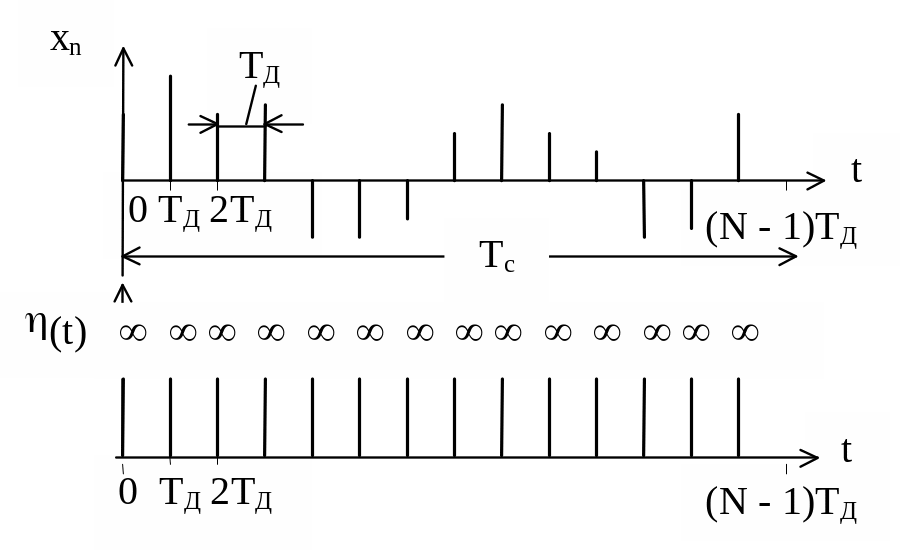
Рисунок 4.1 – Дискретный сигнал и последовательность дельта - функций
Поскольку цифровая обработка сигналов возникла значительно позже аналоговой, то алгоритмы дискретного преобразования Фурье (ДПФ) были разработаны на основе преобразований Фурье аналоговых сигналов.
Прямое преобразование Фурье аналогового сигнала x(t) определяется соотношением
![]() (4.1)
(4.1)
где
![]() -
спектральная плотность сигнала.
-
спектральная плотность сигнала.
Для того чтобы
воспользоваться этим соотношением для
определения прямого ДПФ сформируем
аналоговый сигнал x(t),
умножив xn
на соответствующую
![]() -
функцию последовательности
-
функцию последовательности![]()
![]() ,
,
Подставив (6.2) в (6.1), получим
![]() (4.2)
(4.2)
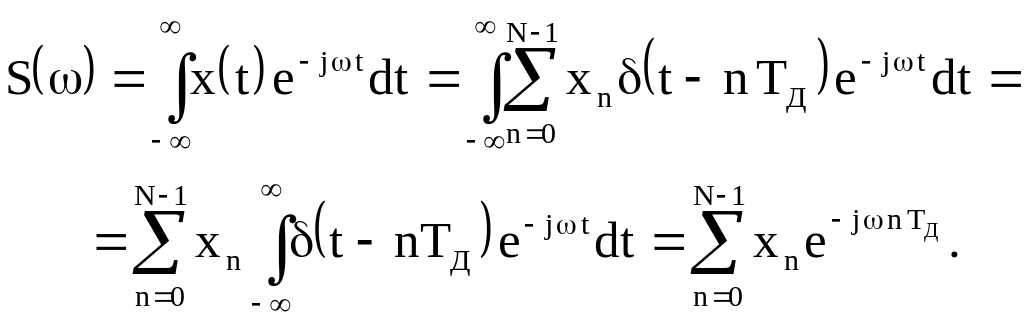
Зададимся шагом изменения частоты = k , где k - целое число
![]()
Учитывая, что TД = Tc / N , получим TД = 2 F Tc / N.
Примем F Tc = 1.
Введем обозначение:
![]()
Тогда
![]() (4.3)
(4.3)
Докажем, что функция
![]() является периодической по k
с периодом, равным N.
является периодической по k
с периодом, равным N.
Действительно,
![]()
Поэтому и Sk представляет собой периодическую функцию с периодом N. Следовательно, k = 0,1,2,.. N-1.
4.2. Обратное дискретное преобразование Фурье Обратное преобразование Фурье аналогового сигнала определяется соотношением
![]() (4.4)
(4.4)
Выражение для обратного преобразования (4.4) отличается от выражения для прямого преобразования (4.1) знаком в показателе экспоненты и постоянным сомножителем перед знаком интеграла.
По аналогии с (4.4) и (4.1) , учитывая (4.3), запишем выражение для обратного ДПФ
![]() (4.5)
(4.5)
где а – неизвестная константа.
Для определения константы a подставим (4.3) в (4.5), предварительно заменив в (4.3) индекс суммирования n на m
![]()
При m = n имеем
![]()
При m
n рассматриваемая сумма представляет
собой сумму членов геометрической
прогрессии, у которой первый член равен
единице, последний
![]() ,
а знаменатель -
,
а знаменатель -
![]()
Поэтому при m
n
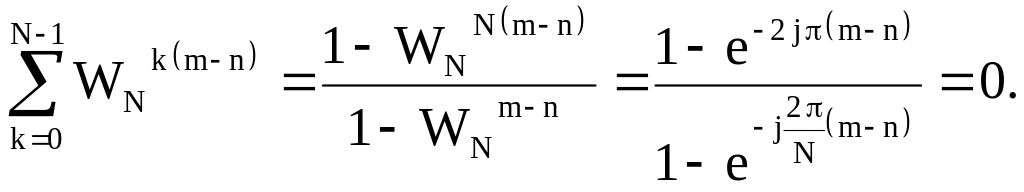
В результате
получим
![]() ,
следовательно,
,
следовательно,
![]() .
.
Таким образом
,
![]() (4.6)
(4.6)
Из (4.3) и (4.6) следует,
что для определения всех N отсчетов
спектра по (4.3) или N отсчетов временной
функции по (4.6) требуется выполнить
![]() комплексных умножений
комплексных умножений
и столько же комплексных сложений. При N больше 1000 это прямое вычисление требует больших затрат машинного времени. Поэтому возникла необходимость в разработке алгоритмов быстрого преобразования Фурье (БПФ), позволяющих уменьшить число арифметических операций.
Лекция №12
4.3. Алгоритм быстрого преобразования Фурье с прореживанием во
времени
Рассмотрим
последовательность xn
, содержащую
![]() отсчётов, где M - целое число (рисунок
4.2). Разобьем члены этой последовательности
на две группы. В первую
отсчётов, где M - целое число (рисунок
4.2). Разобьем члены этой последовательности
на две группы. В первую
включим члены исходной последовательности с нулевым и четными индексами, во вторую - члены с нечетными индексами. Из первой группы образуем последовательность x1m, а из второй - последовательность x2m.
Индексы членов последовательностей xn и x1m связаны соотношением n = 2m, а индексы членов последовательностей xn и x2m - соотношением n = 2m + 1.
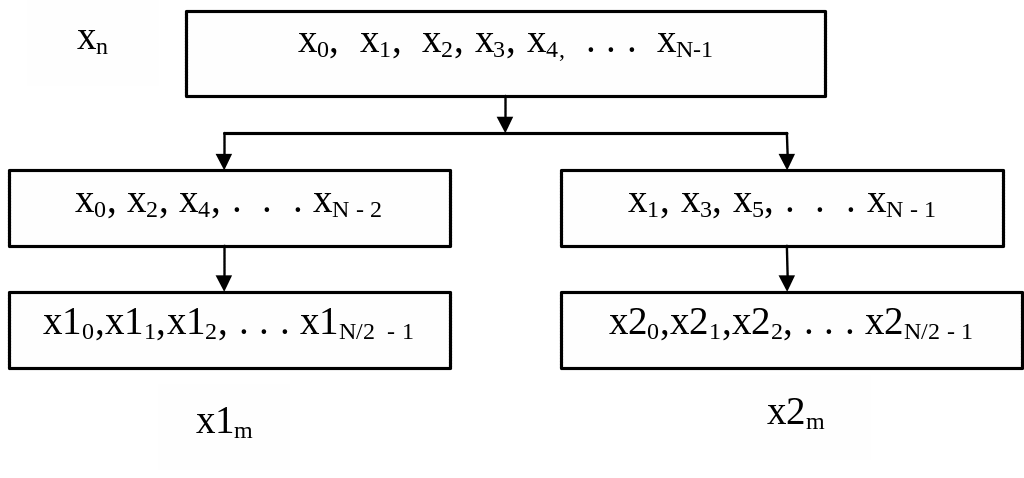
Рисунок 4.2 – Разбиение последовательности отсчетов x на две последовательности
x1 и x2, содержащие члены исходной последовательности x с четными
и нечетными индексами соответственно
Тогда выражение для прямого ДПФ (6.3) можно представить в виде
![]()
Учитывая,
что
![]() ,
получим
,
получим
![]() .
.
Обозначим
![]() - прямое ДПФ последовательности x1
и
- прямое ДПФ последовательности x1
и
![]() -
прямое ДПФ последовательности x2,
-
прямое ДПФ последовательности x2,
где
![]() .
.
Учтем также,
что
![]() ,
а
,
а
![]() .
.
Поэтому
![]() при i = 0, 1, 2, ..
N /
2 - 1 и
k = i,
при i = 0, 1, 2, ..
N /
2 - 1 и
k = i,
![]() при
i = 0, 1, 2, .. N / 2 - 1 и
k = i+N / 2. (4.7)
при
i = 0, 1, 2, .. N / 2 - 1 и
k = i+N / 2. (4.7)
Графическое представление вычислительных операций (4.7) приведено на рисунке 4.3. На нем показано, как из двух четырехточечных последовательностей формируется од-
на восьмиточечная.
Стрелочками представлены множители
![]() ,
на которые умножаются отсчеты S20
, S21
, S22
, S23
соответственно. Отсчеты S0
, S1
, S2,
S3 получаются
с использованием операции сложения,
поэтому около них стоит знак “ + “,
отсчеты S4
, S5
, S6
, S7
находятся после выполнения операции
вычитания и около них поставлен знак
“ - “.
,
на которые умножаются отсчеты S20
, S21
, S22
, S23
соответственно. Отсчеты S0
, S1
, S2,
S3 получаются
с использованием операции сложения,
поэтому около них стоит знак “ + “,
отсчеты S4
, S5
, S6
, S7
находятся после выполнения операции
вычитания и около них поставлен знак
“ - “.
Описанная часть рисунка напоминает развернутые крылья бабочки, поэтому“ бабочкой “ называется данная операция БПФ. В виде таких же бабочек можно развернуть показанные на рисунке блоки ДПФ. Из каждого блока ДПФ получается своя бабочка и два двухточечных блока ДПФ, каждый из которых представляется своей бабочкой. Двухточечные блоки ДПФ дальнейшего разбиения не требуют.
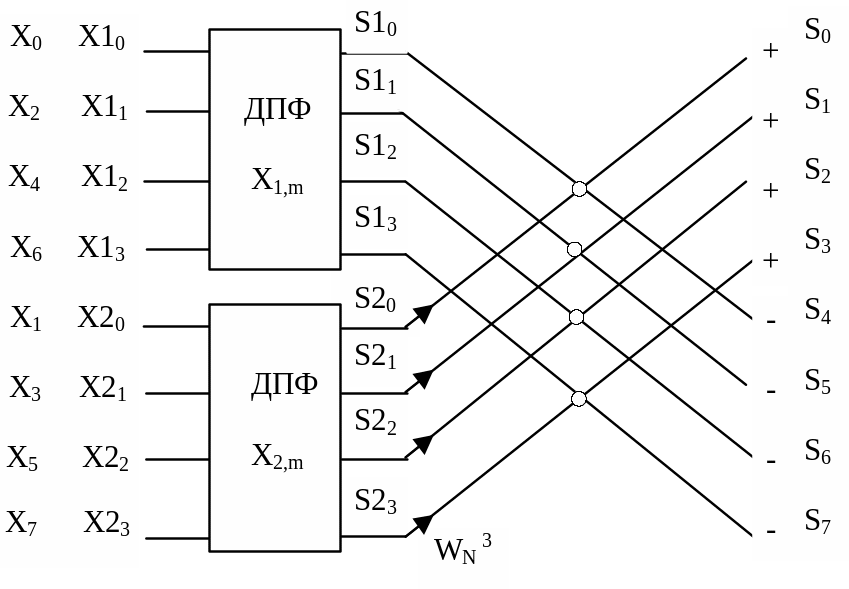
Рисунок 4.3 - Формирование отсчетов спектра восьмиточечной последовательности
из отсчетов спектров двух четырехточечных последовательностей с
использованием прореживания во времени
Подсчитаем количество операций умножения, которые нужно выполнить, используя алгоритм БПФ. Для этого составим таблицу 4.1.
Таблица 4.1
Номер шага разбиения |
Количество умножений на постоянный коэффициент |
Количество блоков ДПФ, подлежащих дальнейшему разбиению |
Вид последовательности на входах оставшихся блоков |
1 |
N / 2 |
2 |
N / 2 |
2 |
2 ( N / 4 ) = N / 2 |
4 |
N / 4 |
3 |
4 ( N / 8 ) = N / 2 |
8 |
N / 8 |
. . . |
. . .
|
. . . |
. . .
|
M -1 |
N / 2 |
2 M -1 |
N / 2 M -1 = 2 |
M |
N / 2 |
- |
- |
Из таблицы видно, что на каждом шаге разбиения выполняется N / 2 умножений, а количество шагов равно M = log 2 N. Следовательно, количество умножений равно
(N / 2) log2 N вместо N2 при ДПФ. Величина выигрыша при переходе от ДПФ к БПФ увеличивается с увеличением количества отсчетов N.
4.4. Алгоритм быстрого преобразования Фурье с прореживанием по
частоте
Вместо изложенной процедуры разбиения множества объектов на объекты с четны-
ми и нечетными номерами можно рассмотреть процедуру разбиения исходного множества на две половины: правую и левую. Последняя процедура и нашла применение в алгоритме БПФ, основанном на прореживании по частоте.
Пусть имеется исходная N - точечная последовательность xn , где N = 2M (рисунок 6.4). Разобьем члены этой последовательности на две группы. В первую включим первую половину членов исходной последовательности, а во вторую группу - вторую половину. Из первой группы образуем последовательность x1m , а из второй - последовательность x2m.
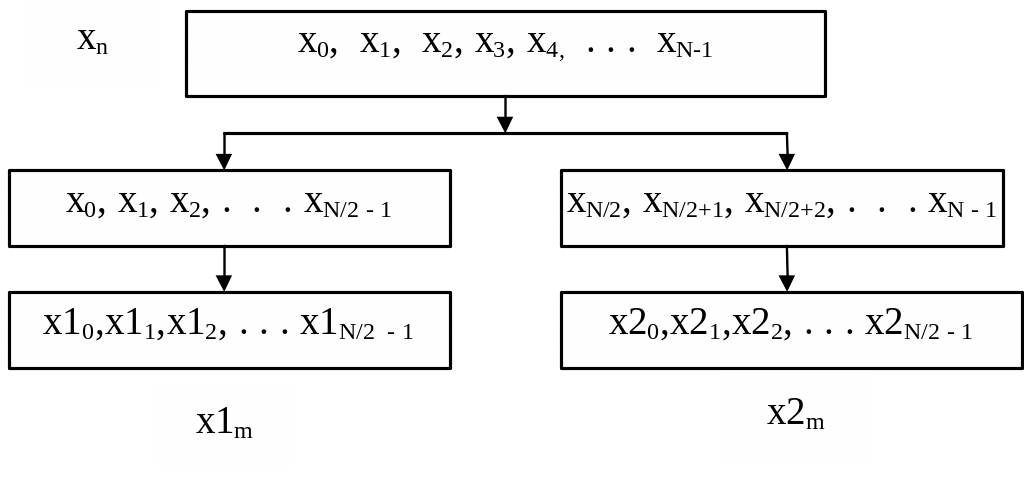
Рисунок 4.4 - Разбиение последовательности отсчетов x на две последовательности
x1 и x2, содержащие первую и вторую половину членов исходной
последовательности соответственно
Индексы последовательностей xn и x1m связаны соотношением n = m, а индексы по-
следовательностей xn и x2m - соотношением n = N/ 2 + m.
Тогда выражение для прямого ДПФ (6.3) можно представить в виде
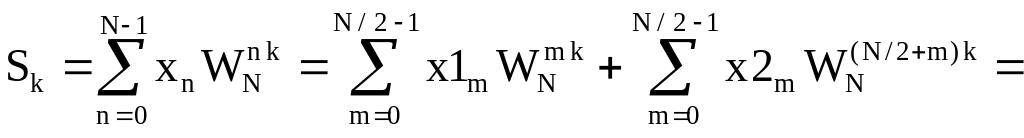
![]() .
.
