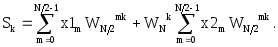4. Преобразование Фурье и вейвлет-преобразование

Введение

Жан Батист Жозеф Фурье (1768...1830), по-видимому, и не подозревал, какую роль будут иметь его ряды и преобразования в обработке телекоммуникационных сигналов. Фундаментальное понятие спектра сигнала связано с рядом и преобразованием Фурье. Исследование линейности телекоммуникационных систем сопровождается определением высших гармоник испытательного синусоидального сигнала по формулам Фурье. Анализ устройств обработки сигналов часто осуществляется с использованием разложения периодических функций в ряды Фурье.

Поэтому появление цифровой обработки сигналов потребовало разработки дискретного преобразования Фурье. В настоящее время дискретное преобразование Фурье используется не только как математический аппарат анализа и синтеза сигналов, но и для цифровой реализации устройств, например, анализаторов спектра, формирователей и демодуляторов сигналов с ортогональным частотным разделением, используемых в цифровом телевидении.

Однако у преобразования Фурье есть один недостаток: невозможность отслеживания изменения спектральной плотности сигнала во времени. Этот недостаток устраняет вейвлет-преобразование.

Данная тема включает следующие разделы:

4.1.Прямое дискретное преобразование Фурье,

4.2.Обратное дискретное преобразование Фурье,

4.3. Алгоритм быстрого преобразования Фурье с прореживанием во времени,

4.4. Алгоритм быстрого преобразования Фурье с прореживанием по частоте,

4.5. Дискретное косинусное преобразование,

4.1.Прямое дискретное преобразование Фурье

На рисунке 4.1 показан дискретный сигнал x_n , содержащий N отсчетов. Длительность сигнала T_c = T_Д N, где T_Д - интервал дискретизации. На этом же рисунке приведена последовательность (t) дельта - функций (t - n T_Д).

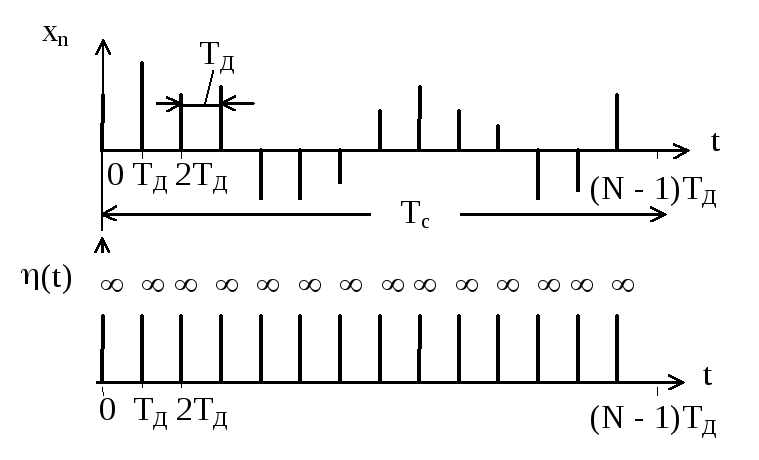
Рисунок 4.1 – Дискретный сигнал и последовательность дельта - функций

Поскольку цифровая обработка сигналов возникла значительно позже аналоговой, то алгоритмы дискретного преобразования Фурье (ДПФ) были разработаны на основе преобразований Фурье аналоговых сигналов.

Прямое преобразование Фурье аналогового сигнала x(t) определяется соотношением

(4.1)

где - спектральная плотность сигнала.

Для того чтобы воспользоваться этим соотношением для определения прямого ДПФ сформируем аналоговый сигнал x(t), умножив x_n на соответствующую - функцию последовательности,

Подставив (6.2) в (6.1), получим

(4.2)

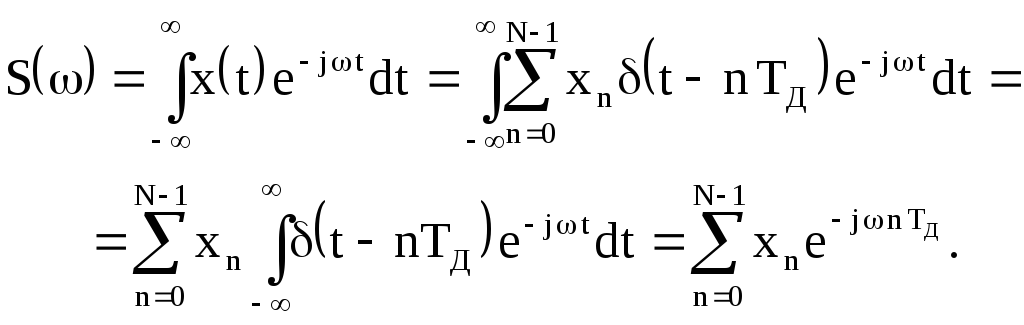
Зададимся шагом  изменения частоты  = k  , где k - целое число

Учитывая, что T_Д = T_c / N , получим  T_Д = 2  F T_c / N.

Примем F T_c = 1.

Введем обозначение:

Тогда

(4.3)

Докажем, что функция является периодической по k с периодом, равным N.

Действительно,

Поэтому и S_k представляет собой периодическую функцию с периодом N. Следовательно, k = 0,1,2,.. N-1.

4.2. Обратное дискретное преобразование Фурье Обратное преобразование Фурье аналогового сигнала определяется соотношением

(4.4)

Выражение для обратного преобразования (4.4) отличается от выражения для прямого преобразования (4.1) знаком в показателе экспоненты и постоянным сомножителем перед знаком интеграла.

По аналогии с (4.4) и (4.1) , учитывая (4.3), запишем выражение для обратного ДПФ

(4.5)

где а – неизвестная константа.

Для определения константы a подставим (4.3) в (4.5), предварительно заменив в (4.3) индекс суммирования n на m

При m = n имеем

При m  n рассматриваемая сумма представляет собой сумму членов геометрической прогрессии, у которой первый член равен единице, последний , а знаменатель -

Поэтому при m  n

В результате получим , следовательно, .

Таким образом , (4.6)

Из (4.3) и (4.6) следует, что для определения всех N отсчетов спектра по (4.3) или N отсчетов временной функции по (4.6) требуется выполнить комплексных умножений

и столько же комплексных сложений. При N больше 1000 это прямое вычисление требует больших затрат машинного времени. Поэтому возникла необходимость в разработке алгоритмов быстрого преобразования Фурье (БПФ), позволяющих уменьшить число арифметических операций.

4.3. Алгоритм быстрого преобразования Фурье с прореживанием во времени

Рассмотрим последовательность x_n, содержащую отсчетов, где M - целое число, Разобьем члены этой последовательности на две группы.

Индексы членов последовательностей x_n и x1_m связаны соотношением n = 2m, а индексы членов последовательностей x_n и x2_m - соотношением n = 2m + 1.

Тогда выражение для прямого ДПФ можно представить в виде

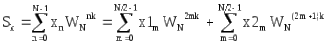
Учитывая, что

,

получим