
4_magnetizm
.pdfЛекции по физике
1 семестр
4 Магнетизм

2 Магнитное поле в вукууме
Магнитное поле в вукууме
Закон взаимодействия элементарных токов
Закон взаимодействия токов гораздо сложнее закона Кулона, поэтому неудивительно, что в его исследовании и открытии приняло участие много учёных. Существенный вклад в эти исследования внесли Био1, Савар2, Ампер3, Лаплас4.
В 1820 году копенгагенский профессор физики Эрстед5 открыл, что проводник с током вызывает появление сил, действующих на магнитную стрелку. При помещении провода с током вдоль магнитной стрелки поверх неё, северный конец стрелки отклоняется в сторону, определяемую по следующему правилу: при расположении правой руки ладонью вниз, четырьмя пальцами по направлению тока, большой палец, отогнутый на 90 , покажет направление отклонения стрелки. При помещении провода с током под магнитной стрелкой, последняя отклоняется в противоположную сторону.
Также в 1820 году Био и Савар сформулировали закон для силы dF действия элемента тока I dl на магнитный полюс, удалённый на некоторое расстояние r:
1Био Жан Батист (21.04.1774-3.02.1862) — французский физик, член Парижской АН (1803). Родился в Париже. Окончил Политехническую школу (1797). С 1800 — профессор Колледж де Франс, в 1808-49 — Парижского университета.
2Савар Феликс (30.06.1791-16.03.1841) — французский физик, член Парижской АН (1827). Родился в Мезьере. Окончил Страсбургский университет (1816), получив медицинское образование. Работал военным хирургом. С 1816 занялся физикой, с 1828
—профессор экспериментальной физики в Колледж де Франс.
3Ампер Андре Мари (22.01.1775-10.06.1836) — французский физик, математик и химик, член Парижской АН (1814). Родился в Лионе. Получил домашнее образование. В 1805-24 работал в Политехнической школе в Париже (с 1809 — профессор), с 1824
—профессор Колледж де Франс.
4Лаплас Пьер Симон (28.03.1749-5.03.1827) — французский астроном, физик и математик, член Парижской АН (1785). Родился в Бомон-ан-Оже. учился в школе бенедиктинцев. В 1771 стал профессором Военной школы в Париже, в 1790 — председателем Палаты мер и весов.
5Эрстед Ханс Кристиан (14.08.1777-9.03.1851) — датский физик, непременный секретарь Датского королевского общества (с 1815). Родился в Рудкёбинге (о. Лангелани). Окончил Копенгагенский Университет (1797). С 1806 — профессор этого университета, с 1829 одновременно директор Копенгагенской политехнической школы.
Закон взаимодействия элементарных токов |
3 |
dF I dl ( )f(r), |
|
где — угол, описывающий взаимную ориентацию элемента тока и магнитного полюса, Функция ( ) была найдена экспериментально,
аf(r) выведена теоретически Лапласом: f(r) r 2.
Вокончательном виде закон Био-Савара-Лапласа был сформулирован в 1826г. в виде формулы для силы, действующей на магнитный полюс, поскольку понятия напряжённости и магнитной индукции магнитного поля ещё не существовало.
В1820г. Ампер открыл взаимодействие токов — притяжение или лтталкивание параллельных токов. Так сонаправленные или текущие в одном направлении токи притягиваются, а противоположно направленные — отталкиваются. Также Ампер доказал эквивалентность соленоида (катушки индуктивности) и постоянного магнита. Таким образом, задача о магнитном взаимодействии свелась к задаче о взаимодействии элементов тока. Данный закон должен был стать аналогом закона Кулона. В настоящее время для взаимодействия токов используется формула полученная не Ампером, а Грассманом в 1844г.:
|
|
I |
2 |
dl |
2 |
|
I dl r |
|
|
I dl |
, I dl ,r |
|
|
|||
dF |
k |
|
|
|
1 1 12 |
k |
2 |
2 |
1 |
1 12 |
|
, |
(1.1) |
|||
|
|
|
|
|
r3 |
|
|
|
r3 |
|
|
|||||
12 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
12 |
|
|
|
|
12 |
|
|
|
|
где dF12 — сила, с которой элемент тока I1 dl1 |
действует на элемент |
|||||||||||||||
тока I2 dl2 ; r12 |
— |
радиус-вектор, |
проведённый от |
элемента |
тока |
|||||||||||
I1 dl1 к элементу тока I2 dl2 .
Сила dF21 , с которой второй элемент тока действует на первый, определяется той же формулой, но со взаимной заменой индексов 1 и 2. Вообще, силы dF12 и dF21 не коллинеарны друг другу, следова-
тельно, взаимодействие элементов тока не удовлетворяет III за-
кону Ньютона: dF12 dF21 0. Дело в том, что реально на любой элемент тока действует не элемент другого тока, а весь замкнутый ток, к которому принадлежит тот элемент. Поэтому III закону Нью-
тона удовлетворяют силы взаимодействия замкнутых токов.

4 Магнитное поле в вукууме
Закон Био-Савара-Лапласа. Сила Ампера
Взаимодействие элементов тока представляется следующим образом: элемент тока I1 dl1 создаёт в точке нахождения элемента тока I2 dl2 магнитное поле, которое действует непосредственно на этот элемент с силой dF12 . Таким образом, магнитное поле элемента тока описывается вектором магнитной индукции:
dB |
k |
I1 dl1 r12 |
k |
I1 dl1,r12 |
, |
(1.2) |
|
r3 |
r3 |
||||||
12 |
2 |
2 |
|
|
|||
|
|
12 |
|
12 |
|
|
а сила, действующая на второй элемент тока, выражается через магнитную индукцию:
dF12 k3I2 dl2 dB12 k3 I2 dl2,dB12 . |
(1.3) |
Для силы, действующей со стороны замкнутого тока, а, следовательно, и для магнитной индукции выполняется принцип суперпо-
зиции: различные участки проводника создают каждый свое магнитное поле. Все вместе создают общее магнитное поле, при этом индукция полей векторно складывается и даёт индукцию В результирующего магнитного поля.
В формуле (1.1) коэффициент пропорциональности k1 определяется произведением коэффициентов пропорциональности k2 в формуле (1.2) и k3 в (1.3): k1 k2 k3. Таким образом, выбор единицы измерения вектора магнитной индукции определяется одним из коэффициентов k2 или k3 , если введена единица измерения силы тока и обоими, если единица силы тока тоже определяется из данных уравнений. При построении магнитной системы единиц СГСМ, основанной на системе СГС, оба последних коэффициента выбираются равными единице. В СГСМ единица силы тока определяется из равенства единице коэффициента в уравнении (1.1): k1 1. Поэтому, единица измерения силы тока и заряда, входящих как в электрические, так и в магнитные явления в системах СГСЕ и СГСМ различны.:
1 СГСМ 29979245800 СГСЕ |
I |
3 1010 |
СГСЕ 10 А. |
I |
СГСМ |
I |
СГСЕ |
c. |
||
I |
|
|
I |
|
|
|
||||
1 СГСМ 29979245800 СГСЕ |
q |
|
3 1010 |
СГСЕ 10 Кл. |
q |
СГСМ |
q |
c. |
||
q |
|
|
q |
|
|
|
СГСЕ |
|
||
Так как такое положение дел не является удовлетворительным, то была введена система единиц Гаусса (в дальнейшем просто система СГС), в которой все формулы и единицы измерения физических величин связанных с электрическими явлениями и с электрическим током совпадают с системой СГСЕ, а единицы измерения физических величин, связанным с магнитными явлениями, совпадают с единицами измерения СГСМ системы единиц. Значения коэффициентов пропорциональности в формулах
(1.1)-(1.3) в различных системах единиц приведены |
в нижеследующей таблице |
|
( c 299 792 458 м с — скорость света в вакууме; |
|
4 10 7 Гн м — магнитная |
|
0 |
|
постоянная): |
|
|

|
Закон Био-Савара-Лапласа. Сила Ампера |
|
|
|
|
|
|
|
5 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Таблица коэффициентов в формулах (1.1)-(1.3) |
||||||||||||
|
Коэффициент |
|
Система СИ |
|
|
|
Система |
|
Система |
|
Система |
|
|
||||||||||
|
пропорциональности |
|
|
|
Гаусса (СГС) |
|
|
СГСМ |
|
СГСЕ |
|
|
|||||||||||
|
|
k2 |
|
|
|
0 4 |
|
|
|
|
|
1 c |
|
|
|
1 |
|
1 c2 |
|
|
|||
|
|
k3 |
|
|
|
1 |
|
|
|
|
|
|
1 c |
|
|
|
1 |
|
1 |
|
|
||
|
k1 k2 k3 |
|
|
|
0 4 |
|
|
|
|
|
1 c2 |
|
|
|
1 |
|
1 c2 |
|
|
||||
|
Так как в систему Гаусса вошли токи и заряды определённые в системе СГСЕ |
||||||||||||||||||||||
(1 СГСI |
1 СГСЕI; 1 СГСq |
1 СГСЕq ), |
то |
в уравнениях |
магнитных |
явлений токи |
и |
||||||||||||||||
заряды |
СГСМ |
системы |
выражаются через |
СГСЕ |
величины: |
|
IСГСМ IСГСЕ |
c, |
|||||||||||||||
|
qСГСМ qСГСЕ c, |
что |
выглядит |
в |
уравнениях |
магнитных явлений |
|
как добавление |
|||||||||||||||
множителей 1 c |
к каждому току и заряду. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
В качестве единицы измерения вектора магнитной индукции в системе СИ вы- |
||||||||||||||||||||||
ступает 1 Тл (Тесла), а в гауссовой системе единиц: 1 СГСB 1 СГСМB 1 Гс (Гаусс). |
|||||||||||||||||||||||
|
1Тл 104 Гс; 1Гс 10 4 Тл. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
С учётом вышеизложенного запишем закон взаимодействия |
||||||||||||||||||||||
элементарных токов6: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
I2 dl2, I1 dl1,r12 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
dF |
|
0 |
|
|
|
|
|
|
|
|
|
|
, |
|
(1.1 ) |
||
|
|
|
|
|
|
4 |
|
|
|
r3 |
|
|
|||||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
где |
4 10 7 Гн м — магнитная постоянная. |
|
|
|
|
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Также запишем выражение для индукции магнитного поля соз- |
||||||||||||||||||||||
данного элементом тока I dr |
— закон Био-Савара-Лапласа7: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
dB(r ) |
|
|
0 |
I dr,(r0 r) |
, |
|
|
(1.2 ) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
4 |
|
|
r r |
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
где r — радиус-вектор элемента тока, r0 — радиус-вектор точки, в которой рассматривается поле.
Сила действующая на элемент тока I dl со стороны магнитного поля с индукцией B получила название силы Ампера8:
dF I dl,B |
(1.3 ) |
6 |
Закон взаимодействия элементарных токов в системе Гаусса (СГС) (с — ско- |
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
рость света в вакууме): dF |
|
|
I2 |
dl2, I1 dl1,r12 |
. |
|
|
|
|
|
|
|
|
||
|
12 |
|
c2 |
r3 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
7 |
Закон Био-Савара-Лапласа в системе Гаусса (СГС): |
dB(r ) |
1 |
Idr,(r0 r) |
. |
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
c |
|
|
r r |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
8 |
Сила Ампера в системе Гаусса (СГС): dF |
1 I dl,B . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|

6 Магнитное поле в вукууме
Закон Био-Савара-Лапласа сформулированный для элемента тока не может быть проверен, поэтому чаще его формулируют для поля замкнутого тока:
B(r ) |
0 |
|
I dr,(r0 r) |
. |
|
|
(1.4) |
||||
4 |
|
|
|
||||||||
0 |
|
r0 r |
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
Учитывая, что Idr jS dl jdV |
(dl |
|
dr |
|
; |
вектора j и dr со- |
|||||
|
|
||||||||||
направлены), получим выражение для индукции магнитного поля объёмных токов:
B(r ) |
0 |
|
j(r),(r0 r) |
dV. |
(1.5) |
|||
4 V |
|
|||||||
0 |
|
r0 r |
|
3 |
|
|
||
|
|
|
|
|
||||
|
|
|
|
|||||
Сила Лоренца. Движение заряда в магнитном поле |
|
|||||||
Учитём, что Idl jS dl jdV qnvdV qvdN (вектора |
j и |
|||||||
dl сонаправлены; n — концентрация зарядов q), положим число частиц dN 1. Тогда сила, действующая на точечный заряд:
F qv,B .
Учитывая, что на заряд помимо магнитного поля действует и электрическое, которые неразрывно связаны друг с другом, получим выражение для силы Лоренца9:
F qE q v,B .
При попадании заряда в магнитное поле, на него начинает действовать сила, перпендикулярная скорости заряда. Т.е. траектория движения заряда является криволинейной. Рассмотрим частный случай нерелятивистского движения заряда в постоянном однородном магнитном поле. В случае, когда скорость заряда перпендикулярна магнитной индукции v B, заряд движется по окружности, радиус которой можно найти из II закона Ньютона, в котором необходимо учесть для ускорения его значение для движения по окружности, а для силы выражение для силы Лоренца:
m |
v2 |
qvB |
|
R |
mv |
. |
R |
|
|||||
|
|
|
|
qB |
||
9 В СГС: F qE q v,B  c.
c.

Взаимодействие прямых токов. 1 Ампер |
7 |
Если угол между скоростью заряда и вектором магнитной индукции отличен от нуля, то для кривизны траектории (!) получим:
m |
v2 |
qvBsin |
|
R |
mv |
. |
|
R |
qBsin |
||||||
|
|
|
кр |
|
|||
|
кр |
|
|
|
|
|
Однако, в этом случае траекторией заряда будет спираль радиусом R (радиус цилиндрической поверхности на которой находится спиральная траектория) и шагом h (расстояние между двумя ближайшими точками траектории вдоль образующей цилиндрической поверхности). Для нахождения параметров спиральной траектории разложим движение на две составляющие: поступательное движение вдоль поля со скоростью v vcos и вращения по окружности со скоростью v vsin в плоскости, перпендикулярной полю. Во втором случае радиус окружности:
R mv mvsin . qB qB
Период обращения:
T |
2 R |
|
2 |
|
mv |
|
2 m |
|
|
|
|
|
. |
||||
v |
v |
qB |
qB |
|||||
|
|
|
|
|
|
|
|
|
Шаг винтовой траектории:
h v T 2 m vcos . |
|
|
qB |
|
|
Следует заметить, что при уменьшении угла между полем и скоростью (при условии  2) радиус винтовой траектории уменьшается, а радиус кривизны траектории увеличивается.
2) радиус винтовой траектории уменьшается, а радиус кривизны траектории увеличивается.
Взаимодействие прямых токов. 1 Ампер
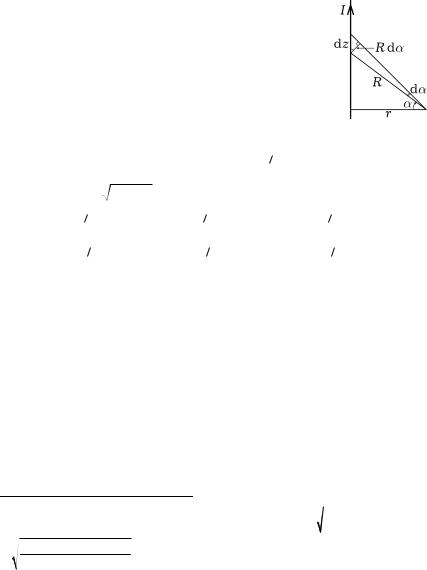
Рассмотрим поле прямого тока идущего из бесконечности и уходящего в бесконечность10. Пусть провод с током расположен вдоль оси Oz и течёт в положительном направлении данной оси, а точка наблюдения находится на расстоянии r от провода в точке (r,0,0).
10 Подразумевается что данный ток в бесконечности замыкается, но так как это происходит в бесконечно далёкой области, то интегрирование по данному пути даёт пренебрежимо малый вклад в закон Био-Савара-Лапласа.
8 Магнитное поле в вукууме |
|
|
|
|
|
|
|
Таким образом, r zez; |
dr ez dz; |
r0 r ex; |
|||||
dr,(r0 r) |
|
ex |
ey |
ez |
|
eyrdz. |
|
|
|
||||||
|
0 |
0 |
dz |
|
|||
|
|
|
r |
0 |
z |
|
|
Вектор магнитной индукции лежит в плоскости, перпендикулярной проводнику и перпендикулярен линии, опущенной из рассматриваемой точку поля на провод с током. На рисунке ось Oz направлена вверх, ось Ox — вправо, Oy — «от нас». Таким образом в искомой точке вектор магнитной индукции направлен «от нас». Значение магнитной индукции:
|
|
|
dz |
|
|
0 |
|||
By |
|
Ir |
|
. |
4 |
r2 z2 3 2 |
|||
Учитывая R 
 r2 z2 r
r2 z2 r cos и dz Rd
cos и dz Rd  cos , получим
cos , получим
|
|
2 |
Rd |
|
|
|
|
|
2 |
cos2 d |
|
|
|
|
I 2 |
|
|||||||
By |
0 |
Ir |
|
|
|
|
|
0 |
Ir |
|
|
|
|
0 |
|
|
|
|
cos d |
||||
4 |
R3 cos |
4 |
r2 cos |
4 r |
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
I |
|
|
|
|
|
|
|
2I |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
sin |
|
|
|
|
|
0 |
|
|
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
4 r |
2 |
sin |
|
4 |
r |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
Если поместить параллельно первому проводнику второй на расстоянии r, то в каждой точке второго проводника вектор магнитной индукции будет перпендикулярен ему и постоянен. Таким образом, сила, с которой первый проводник воздействует на второй равна:
F I lB |
0 |
|
2lI1I2 |
. |
(1.6) |
|
|
||||
2 |
4 |
|
r |
|
|
|
|
|
|||
В случае равных значений сил токов из данной формулы можно определить единицу измерения силы тока (в СИ). Так сила тока в
1 Ампер11 — сила неизменного тока, который проходя по двум
11 |
В СГС: F |
1 2lI I |
|
F |
2lI2 |
|
I |
|
rF |
|
|
|||
|
|
1 2 |
. |
В СГСМ: |
|
|
|
и сила тока |
||||||
|
2 |
|
|
r |
2l |
|||||||||
|
|
c |
|
r |
|
|
|
|
|
|
|
|||
1А  100см 2 10 7 105 дин 0.1дин1
100см 2 10 7 105 дин 0.1дин1 2 0.1СГСМ-ед. силы тока.
2 0.1СГСМ-ед. силы тока.
200см

Напряжённость магнитного поля |
9 |
параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенного на расстоянии 1 м друг от друга в вакууме, вызывает на каждом участке проводника длины 1 м силу взаимодействия 2 10 7 Н.
Из определения 1 Ампера и (1.6) следует выражение для 0 :
|
|
4 rF |
|
4 1м 2 10 7 |
Н |
7 |
Гн |
|
|
||
|
|
|
|
|
|
|
|
4 10 |
|
. |
(1.6) |
2lI I |
|
2 |
1м 1А2 |
|
м |
||||||
0 |
|
2 |
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
Единица измерения 0 будет введена позднее.
Напряжённость магнитного поля
Для описания магнитного поля наряду с вектором магнитной индукции используется другая векторная физическая величина — напряжённость магнитного поля. Если B — магнитная индукция в какой-либо точке поля в вакууме, то напряжённостью магнитного поля в той же точке является величина12:
H B 0 .
0 .
Единицей измерения напряжённости магнитного поля служит Ампер делённый на метр: [H]СИ 1А м.
м.
Выразим закон Био-Савара-Лапласа для напряжённости магнитного поля через токи:
H(r) |
|
I |
|
dr r r |
(1.7) |
|||||||||
|
4 |
|
|
r r |
|
3 |
|
|||||||
|
|
|
|
|||||||||||
и через объёмные токи13: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H(r) |
j(r ) r |
r |
|
dV. |
(1.7 ) |
|||||||||
|
r r |
3 |
|
|||||||||||
|
V |
4 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Зная напряжённость магнитного поля созданного токами, можно найти индукцию умножением на размерный коэффициент 0 и на
12 |
В СГСМ |
— безразмерная величина, равная единице. Тогда H B. Едини- |
||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цей измерения напряжённости магнитного поля является 1 Эрстед: |
||||||||||||||||||||||||
[H] |
|
1Э |
1 |
|
103 А м 79.6А м; |
[H] |
|
1А м 4 10 3 Э 12.6 10 3 Э. |
||||||||||||||||
|
|
СГС |
|
4 |
|
|
|
|
|
|
|
|
СИ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
13 |
В СГС: H(r) |
I |
|
dr r r |
; H(r) |
1 |
|
|
j(r |
|
) r |
r |
dV. |
|||||||||||
|
c |
|
|
r r |
|
3 |
c |
|
|
r r |
|
3 |
|
|||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10 Магнитное поле в вукууме
величину магнитной проницаемости среды , в которой находится рассматриваемая точка поля14:
B 0H. |
(1.8) |
Магнитная проницаемость среды есть величина безразмерная и показывающая во сколько раз увеличивается магнитное поле за счёт присутствия среды. Более подробно напряжённости магнитного поля и магнитная проницаемость среды будет рассмотрена в теме «магнетики».
Применение закона Био-Савара-Лапласа
Магнитное поле в центре кругового витка
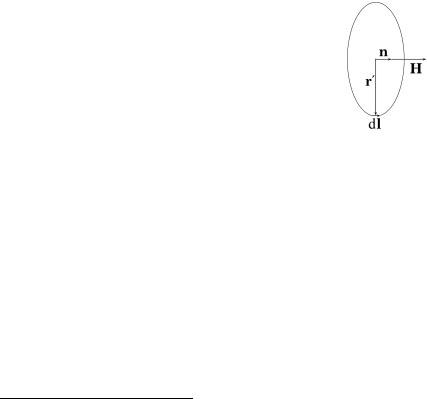
Рассмотрим круговой проводник в форме окруж-
ности с |
током I и радиусом R. Все элементы тока |
dl dr |
перпендикулярны радиус вектору r r . |
Поместим начало координат в центр кругового проводника r 0. Определим вектор нормали в начале координат как единичный вектор, перпендикулярный плоскости кругового витка и составляющий с направлением тока правило правого винта. Из закона Био-
Савара-Лапласа (1.7) получим значение напряжённости магнитного поля в центре кругового проводника15:
H |
I |
|
dr r |
|
I |
|
dl |
n |
I 2 R |
n |
I |
n. |
(1.9) |
|||||
4 |
|
r |
3 |
4 |
2 |
4 |
|
R |
2 |
2R |
||||||||
|
|
|
|
|
|
R |
|
|
|
|
|
|
||||||
Магнитное поле на оси кругового витка
Все элементы тока dl dr кругового проводника с током I и радиусом R перпендикулярны радиус вектору r r . Так же поместим начало координат в центр кругового проводника. Определим значение вектора напряжённости магнитного поля на оси кругового проводника (на прямой проходящей через центр окружности и перпендикулярной ей) на расстоянии h от плоскости витка r hn. Рассмотрим поле созданное двумя одинаковыми элементами тока
14 |
В СГС: B H. |
|
|
|
|
|
|
|
|
|
15 |
В СГС: H |
1 |
I |
dr r |
|
2 I |
n. |
|||
|
c |
|
r |
|
3 |
cR |
||||
|
|
|
||||||||
