
- •1. Общие правила комбинаторики.
- •2. Выборки без повторений (размещения, перестановки и сочетания)
- •3. Случайные события и действия над ними.
- •4. Вероятность события. Статистическое определение вероятности.
- •5. Классическое определение вероятности.
- •6. Свойства вероятностей.
- •7. Теорема сложения вероятностей (для совместимых и несовместимых событий) и следствия из нее.
- •8. Условная вероятность. Теорема умножения вероятностей.
- •9. Независимые события. Теорема умножения вероятностей независимых событий.
- •10. Формула полной вероятности.
- •11.Формула Байеса.
- •12. Независимые повторные испытания, формула Бернулли.
- •13. Локальная теорема Лапласа.
- •14.Теорема Пуассона.
- •15. Интегральная теорема Лапласа.
- •16. Функция Лапласа, ее свойства и график.
- •17. Применение интегральной теоремы Лапласа и функции Лапласа к вычислению вероятностей
- •18. Геометрическое определение вероятности. (без рисунка).
- •19. Случайные величины. Закон распределения дискретной случайной величины.
- •20. Биноминальное распределен.
- •21. Математическое ожидание дискретной случайной величины и его свойства.
- •22. Дисперсия дискретной случайной величины и ее свойства.
- •23. Среднее квадратическое отклонение (ско) и его свойства.
- •24. Математическое ожидание и дисперсия биноминального рас.
- •26. Плотность вер-ти и ее свойства. Связь с ф-ией распределения.
- •27. Нормальное распределение. Нормальная кривая. Вероятность попадания нормально распределенной случайной величины в интервалы и . Правило трех сигм.
- •28. Числовые хар-ки непрерывной случайной величины.
- •29. Математическое ожидание и дисперсия нормального распределения.
- •30. Неравенство Чебышева.
- •31. Теорема Чебышева и ее практическое применение.
- •32. Теорема Бернулли. Сходимость по вероятности.
- •33. Статистическое распределение выборки. Полигон и гистограмма.
- •34. Статистические оценки параметров распределения.
- •35. Выборочное среднее.
- •36. Выборочная дисперсия как оценка теоретической дисперсии, ско, «направленное» ско.
- •37. Доверительная вероятность и доверительный интервал.
- •38. Доверительный интервал для мо нормального распределения при известном и неизвестном .
- •39. Доверительный интервал для математического ожидания нормального распределения.
- •40. Статистическая проверка статистических гипотез. Эмпирические и теоретические частоты. Критерий согласия Пирсона.
- •41. Функциональная, статистическая и корреляционная зависимости.
- •42. Линейная корреляция. Уравнение прямой регрессии.
- •43. Выборочный коэффициент корреляции и его свойства.
11.Формула Байеса.
Пусть событие А может произойти с одним и только с одним из попарно несовместных событий гипотез В1,…,Bn образующих полную группу. Пусть известно, что произошло событие А. Этот факт может повлиять на вероятности гипотез, т. е. произойдет их переоценка. Найдем усл. вер-ть гипотез при условии что произошло событие А. Р(АВi)=Р(А)*РА(Вi)=Р(Вi)*РВi(А); РА(Вi)= Р(Вi)* РВi(А)/Р(А), или используя формулу полной вероятности:

12. Независимые повторные испытания, формула Бернулли.
Пусть
произведено n независ. Испытаний.
Вероятн. Появл. События А в каждом
испытании равна р, а значит вероятность
его непоявления q=1-p.
Найдем вероятность события В, сост. в
том, что в этих испытаниях событие А
появится m раз, вероятн. событ. В обознач.
Pn(m)=P(B).
Аi
-
появление события А в i - том испытании![]() -не
появление А в i-
ом испытании.
-не
появление А в i-
ом испытании.
![]() Здесь
в каждом произведении события Аi
входит n раз, а Ai
(с чертой) m-n
раз. Число таких комбинаций столько,
сколькими способами м. выбрать из n
испытаний те m
в котор. произошло событ. А. Вероятность
каждой такой комбинации по теореме о
умножении независимых событий=рmqn-m,
Здесь
в каждом произведении события Аi
входит n раз, а Ai
(с чертой) m-n
раз. Число таких комбинаций столько,
сколькими способами м. выбрать из n
испытаний те m
в котор. произошло событ. А. Вероятность
каждой такой комбинации по теореме о
умножении независимых событий=рmqn-m,
![]()
По формуле бинома Ньютона имеем:
![]()
13. Локальная теорема Лапласа.
Если вероятность появления события А в каждом из n независимых испытаний постоянно и равна p (0<p<1), то вероятность появления события А в этих испытаниях m раз приближенно =
![]()
где
![]()
Для функции

составлены
специальные таблицы при х из[0, 4), при
x<0 пользуются четностью, при x>=4
полагают
![]() ,
т.к. функция быстро убывает. Ф-я четная.
Формулой пользуются, если npq10.
Формула Лапласа дает более точный рез-т
при р близких к 0,5, если p
или q
мало то погрешность м.б. большой. В этих
случаях используют ф-лу Пуассона.
,
т.к. функция быстро убывает. Ф-я четная.
Формулой пользуются, если npq10.
Формула Лапласа дает более точный рез-т
при р близких к 0,5, если p
или q
мало то погрешность м.б. большой. В этих
случаях используют ф-лу Пуассона.
14.Теорема Пуассона.
Ф-лу используют если p или d мало. Пусть для опред-ти мало p, и вер-ть появления события А удовлетвор. Условию np=λ-const, с такой ситуацией встреч при редких явлениях.
Теорема: Пусть вероятность появления события А в серии из n независимых испыт. равна p=λ/n, тогда вер. появления события А в этой серии m раз удовл. условию:
![]()
(далее переписать эту формулу без предела). Ей пользуются при больших n и малых p и λ 10.
15. Интегральная теорема Лапласа.
Пусть вероятность появления события А в каждом из n независимых испытаний постоянна и = р-const, тогда вероятность того, что в этих испытаниях события А появится не менее m1 и не более m2 раз приближенно =

где
![]()
Эти приближенные формулы будут тем точнее, чем больше число испытаний m, обычно ими пользуются когда npq10.
16. Функция Лапласа, ее свойства и график.
Ф-я из интегральной теоремы Лапласа не интегрируется в конечном виде, поэт. вводят ф-ю:
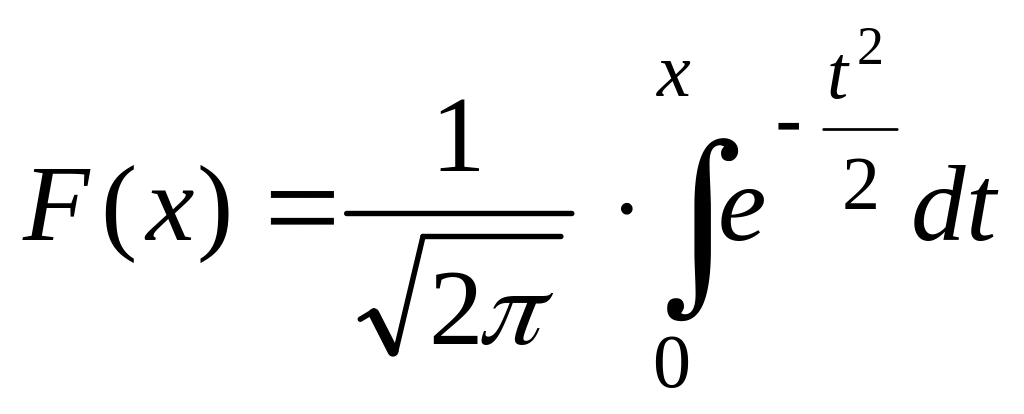
(лучше писать русскую Ф)
Свойства: 1) F(0)=0, 2) F(-x)=-F(x) 3) F(x) - монотонно возрастает, т.к.
![]()
- положит. ф-я. 4) lim (x+)F(x)=1/2;
lim (x-)F(x)=-1/2. График:
Для нее составлены таблицы при x[0;5] F(5)=0,499995, при x>5 F(x) = 0,5, при x<0 пользуются ее нечетностью.
![]() ;
;![]() ;
;
![]() ,
,
этой формулой пользуются при больших n и npq10.
17. Применение интегральной теоремы Лапласа и функции Лапласа к вычислению вероятностей
![]() .
.
![]()
Этой формулой пользуются при больших n и при npq=>10.
Пусть производится n независ. испыт., в кажд из к-рых вер-ть появл. соб. А = p. Мы знаем, что при большом числе испыт. относит. частота соб. А близка к его вероятности. Найдем вер. того, что относит. частота отличается от вер-ти не более чем на Е0, т.е.
![]()
-(m/n)-p; -+p(m/n)+p; np-nmnp+n; (k1=np-n, k2=np+n); к1mk2.
Вычислим:
![]() ;
;
![]() ;
;
x’= - x’’;
![]()
