41. Функциональная, статистическая и корреляционная зависимости.

2 случайные величины м.б. связаны функциональной или статистической зависимостью, или м.б. независимы. 2 величины связаны функциональной зависимостью, если значение одной из них может точно указать значение другой. В ТВ имеют дело обычно со статистической зависимостью, когда зная значение одной величины нельзя указать точное значение другой, а можно указать только закон ее распределения, завис. от того какое знач. приняла 1 велич. Част. случ. статистич. завис. явл. корреляционная завис., когда при изменен. одной велич. измен. сред. знач. др. Пусть знач. х велич. Х соотв. сред. знач.велич. У: у₁,у₂,…,у_m. Условным средним наз.сред. арифмет.знач. велич. У соотв-их знач. велич. X

.

Т.обр. усл. сред. явл. функцией от у, т.е. (1)

Корреляционной зависимостью У от Х наз. функциональн. завис.условного среднего от Х. Уравнение (1) - называют уравнением регрессии У на Х. Функция f(x) - регрессией У на Х, а ее график - линией регрессии У на Х. Аналогично, м. рассм. корреляционную завис. Х на У, т.е.

.

Перед теорией корреляции стоят две основные задачи:

1) найти вид корреляц-ой завис., т.е. вид функции f(x) (линейная, квадратичная, …). Если обе линии регрессии прямые, то корреляция называется линейной. Эта задача носит название регрессионного анализа.

2) установить тесноту, т.е. силу связи между У и Х. О силе связи судят по степени рассеивания знач. У вокруг условн. средних. Чем меньше тем связь сильнее. Эта задача называется корреляционным анализом.

42. Линейная корреляция. Уравнение прямой регрессии.

Пусть Х или У связаны линейной корреляционной зависимостью, т.е. обе линии регрессии прямые. Произведено n испытаний, в результате которых получено следующие пары значений (х1, у1), (х2, у2), … , (хn, уn). Для простоты будем считать, что каждое из значений хi, yi встретилось по одному разу (дальнейшие выводы верны и в общем случае). Обычно экспериментальные данные дают отклонение, связанные со случайными факторами. Наша цель найти уравнение прямой, наилучшим образом приближенной к экспериментальным данным. Т.к. значение не повторяется, то

.

Будем искать выборочное уравнение прямой регрессии в виде

,

коэффициент называют выборочным коэффициентом регрессии У на Х. Наша цель провести прямую так, чтобы она была ближе к экспериментальным точкам. Эта задача решается методом наименьших квадратов и заключение в том, что сумма квадратов отклонений должна быть наименьшей т.е. нужно найти минимальную ф-ии

; ;

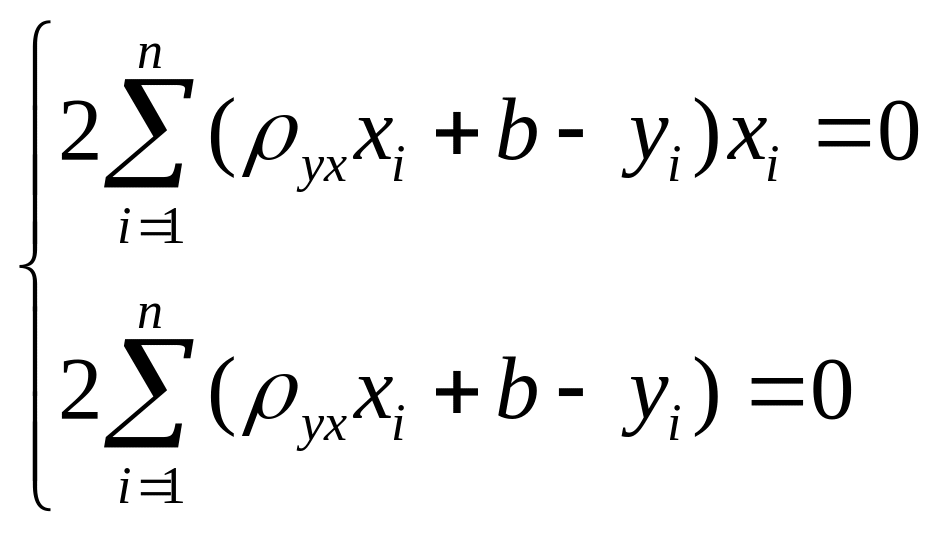
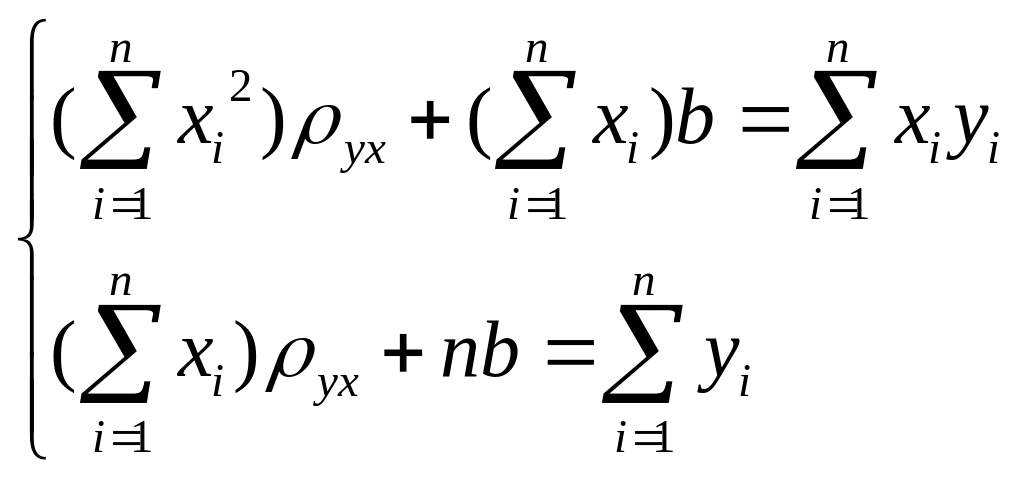
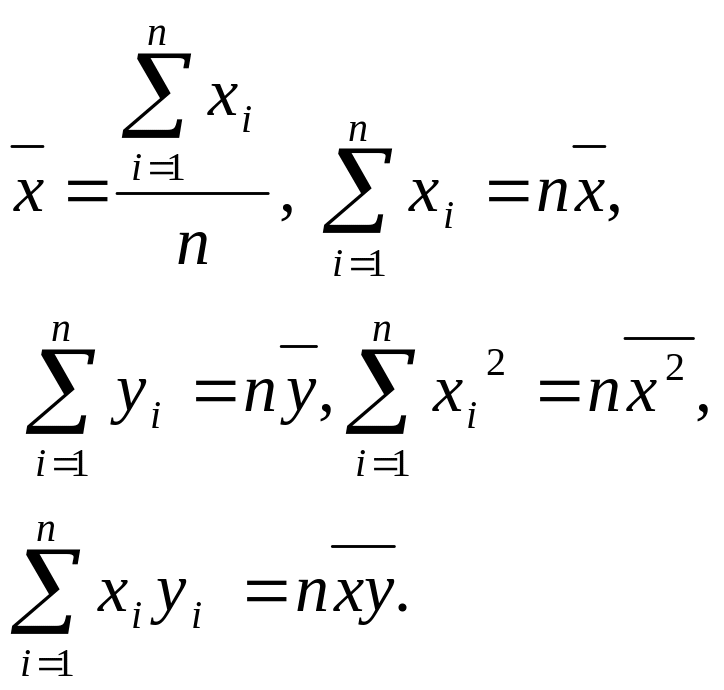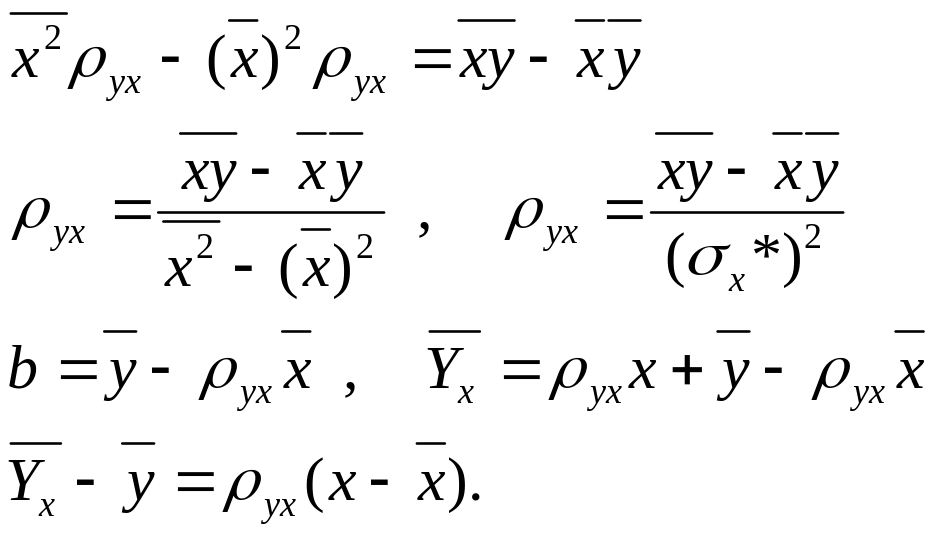
Замечание: аналогично можно получить выборочное уравнение прямой регрессии Х на У.

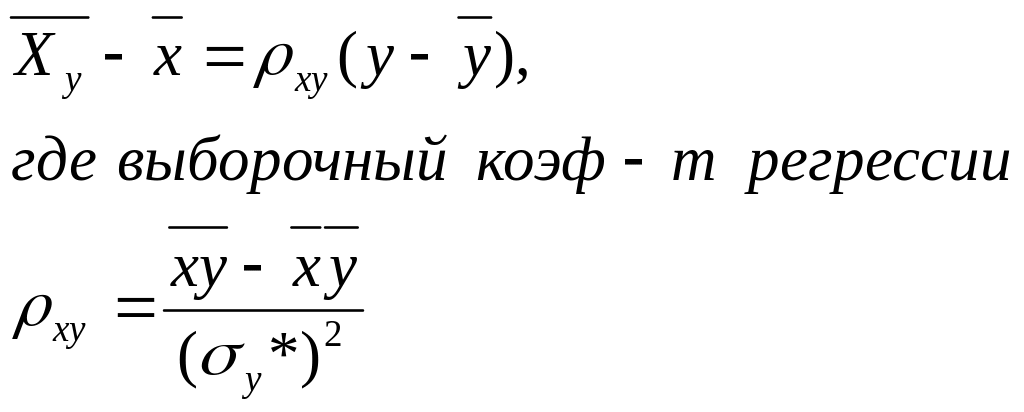
43. Выборочный коэффициент корреляции и его свойства.

Выборочным коэффициентом корреляции наз-ся число

Отсюда

Свойства:

1. | r*|<=1.

2. Если r*=0, и выборочные линии регрессии прямые, Х и У не связаны лин. корреляционной завис. Тогда ур-е прямых регрессии 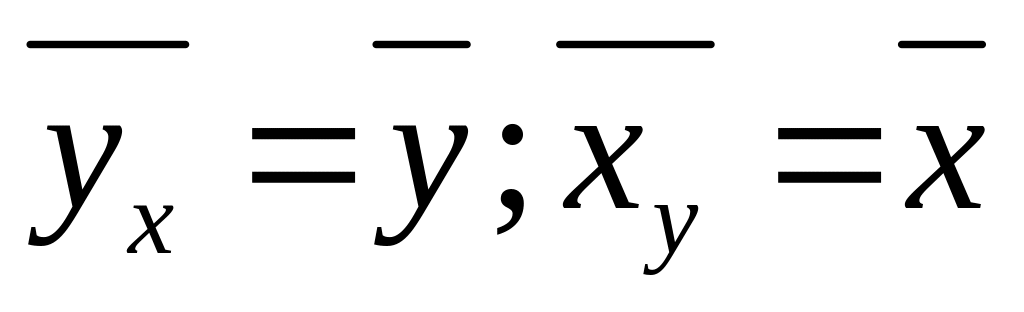Они м.б. просто коррелируемы, но не линейны. В эт.случ.условное сред.одной велич. не зав. от др.

3. Если |r*|=1, то наблюдаемое значение величин Х , У связ. лин. функцион. завис., т.е. они все лежат на одной прямой.

4. При увелич. |r*| лин. корреляц. завис-ть стан-ся все сильнее, превращаясь в функцион-ю при |r*|=1.

Вывод: коэффициент корреляции указывает на степень линейной корреляции, силу связи м/у случ. велич., чем он >, тем связь сильнее, чем ближе к нулю, тем слабее.