3.2. Исходные данные и общие выражения для вектора оценки и ковариационной матрицы

Математическая модель измеряемой величины является параметрической и имеет следующий вид

где – вектор коэффициентов,

– транспонированный вектор-столбец базисных функций.

План измерений задается и имеет следующую структуру: – дискретные значения аргумента t, в которых производится однократное измерение функции отклика. Таким образом, объем многократных измерений по данному плану равно n = l. Предполагается, что многократные измерения являются равноточными и некоррелированными.

Из теории обработки многократных измерений известно, что оценка вектора представляется следующим выражением

, (3.1)

где

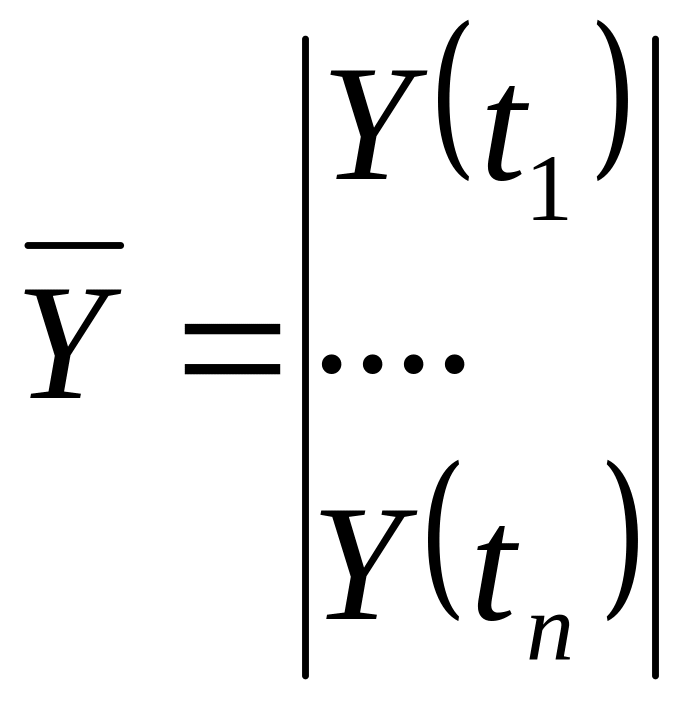– вектор многократных измерений,

– результат измерения при t = t_k, k = ,

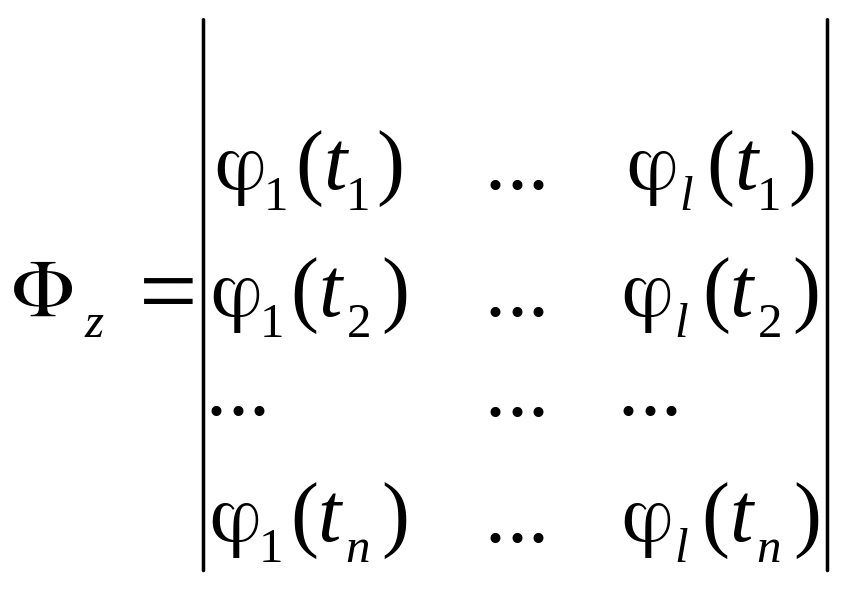– матрица базисных функций размера nl, (3.2)

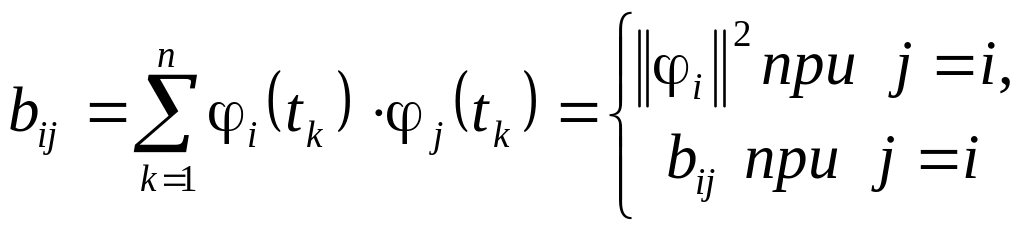(3.3)

где – квадрат нормы базисной функции _i(t), соответствующий заданному плану измерений t_k,

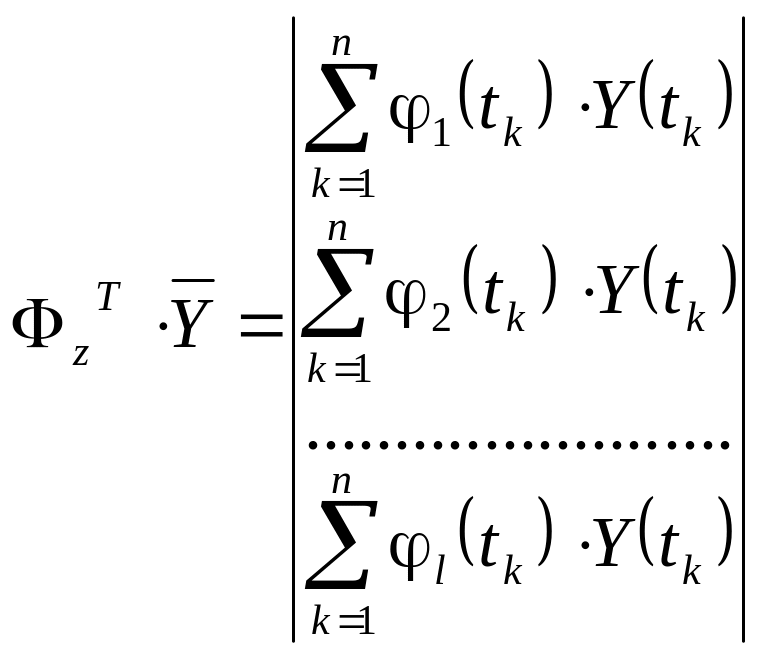– вектор-столбец размера l1.

Если план измерений таков, что при , то он называется ортогональным. Для такого плана измерений оценки коэффициентов имеют наиболее простой вид, а именно:

(3.4)

где – весовые коэффициенты (3.5)

Ковариационная матрица случайного вектора оценки (3.1) равна следующему выражению

Если план измерений ортогональный, то ковариационная матрица будет диагональной размера .

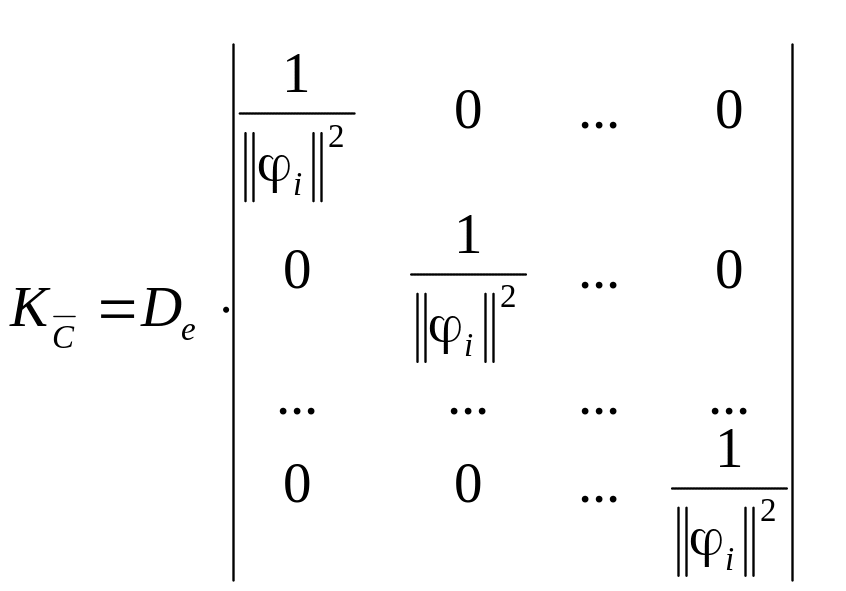
Для такой матрицы выражения для дисперсии оценок коэффициентов будут равны

(3.6)

А дисперсия оценки функции примет следующий вид

(3.7)

где значение дисперсии берется равным значению, полученному по формуле (2.19).

3.3. Определение выражений для оценок коэффициентов и их дисперсии

В соответствии с заданием на интервале [0, Т] оси абсцисс строится план измерений и соответствующие ему значения базисных функций. Затем, формируется матрица базисных функций , и на ее основе определяются элементы матрицы согласно выражению (3.3). Результаты расчетов представляются матрицами и . В силу того, что матрица является диагональной, то алгоритм определения оценок представляется уравнением (3.4) с весовыми коэффициентами, определяемыми выражениями (3.5).

Дисперсии оценок коэффициентов и оценки функции отклика (математической модели измеряемой величины) рассчитываются на основе выражений (3.6) и (3.7).

Пример 3.1. Пусть – математическая модель измеряемой величины x(t) и – план измерений, где n = 2, – интервал планирования измерения.

Базисными функциями модели являются

Найдем элементы матрицы базисных функций

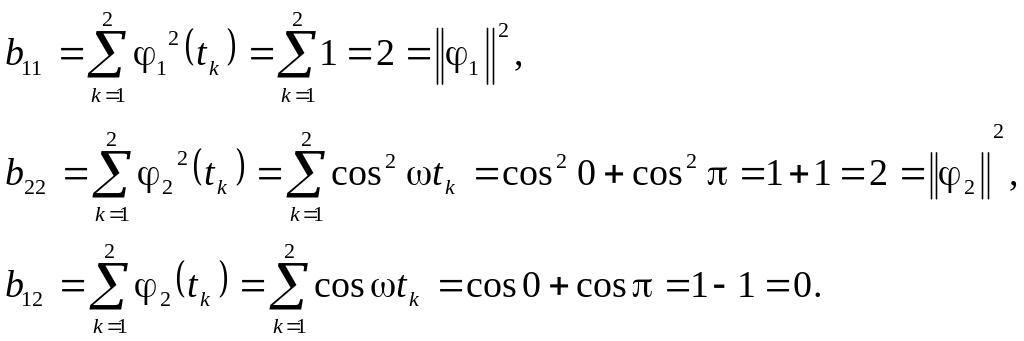
Таким образом, план измерений является ортогональным. Найдем выражения для оценок коэффициентов. Согласно выражению (3.5) получим

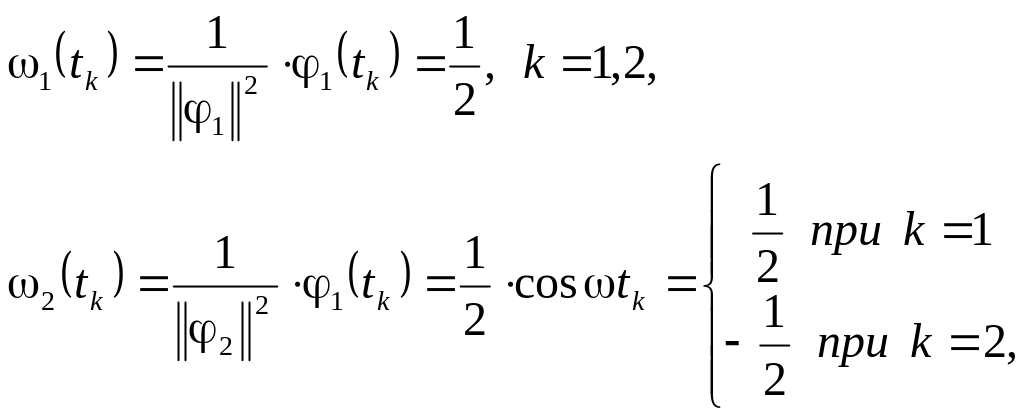
тогда будем иметь

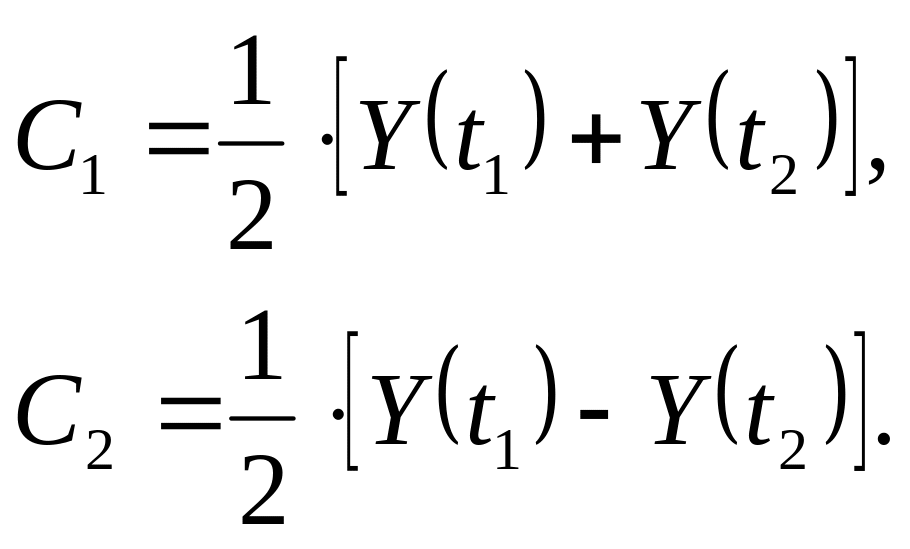
Найдем выражения для дисперсии оценок коэффициентов, используя уравнение (3.6)

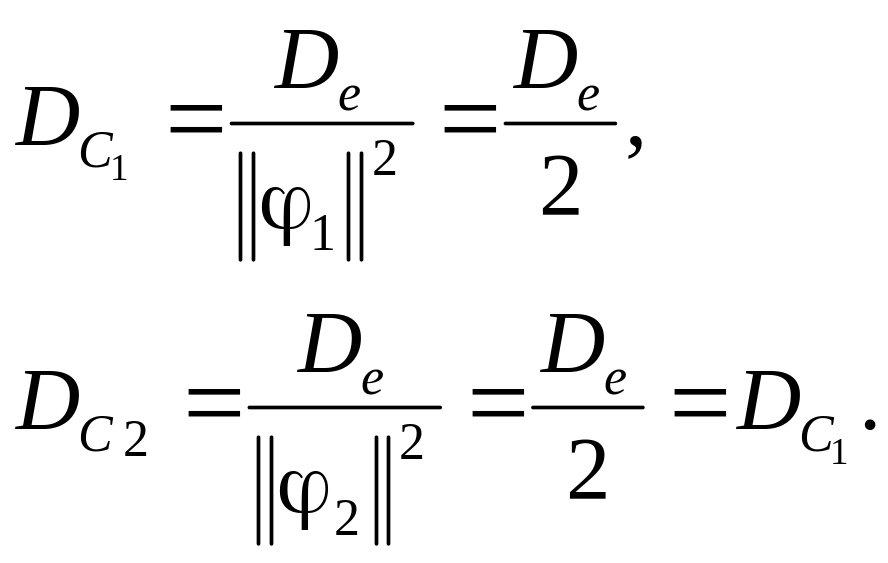
Дисперсия оценки математической модели будет равна (в соответствии с выражением (3.7))

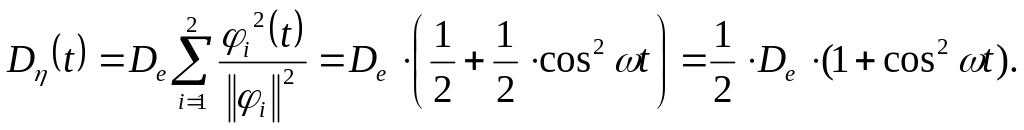
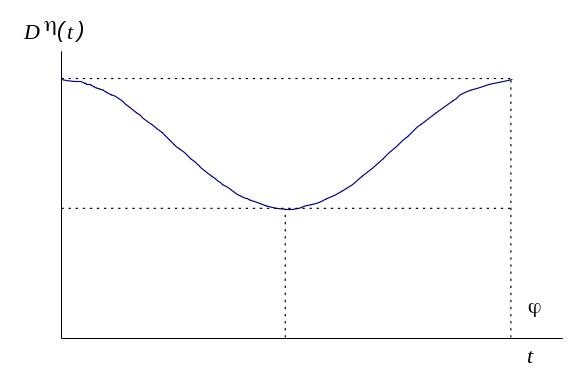
Графическое изображение дисперсии показано на рис. 3.1

D_e

0



Рис. 3.1 - График дисперсии оценки математической модели

Выполнение этого раздела завершается формулами для оценок С_i, и дисперсии и и графиком функции .