7.2. Гистограмма распределения элементов в серии

Чтобы определить, сколько и каких резисторов находится в выборке из 100 резисторов с номинальным значением R_н = 33 Ом с допуском 20 %, проводим ряд измерений и строим гистограмму значений резисторов данной серии.

Значения сопротивлений выборки группируются около среднего значения, появляются с определенными частотами.

Гистограмма выборки представляет собой график, на оси Х которого откладываются значения исследуемой величины, например, сопротивления резистора R_i, на оси Y – числа, характеризующие вероятность появления (частоту попадания в интервал или %) того или иного значения сопротивления.

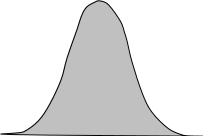
Кривая, описывающая частоту появления значения в серии, в идеальном случае имеет колоколообразную форму (рис. 7.1) и называется кривой нормального распределения (кривая Гаусса, кривая Лапласа).

Математически кривая описывается выражением

, (7.1)

где σ – среднее квадратическое отклонение; Х – переменная; X_вер – наиболее вероятное значение, соответствующее в идеальном случае среднему значению выборки.

f, %



2

Х

X_вер

Рис. 7.1

Характеристики данного распределения описаны в рекомендуемой литературе [21, 22].

Извество, что 99,73 % площади под кривой лежит в пределах шести средних квадратических отклонений σ (рис. 7.1), т. е. по три средних квадратичных отклонения в каждую сторону от среднего значения (правило 3σ). Таким образом, за пределами трехсигмовых значений лежит не более 0,155 % значений искомого распределения. Аналогично 95,49 % площади лежит в пределах четырех σ; 68,32 % площади – в пределах не более 2σ.

Проведя необходимые измерения и построив гистограмму значений резисторов данной серии, определяем среднеквадратичное отклонение, характеризующее искомые параметры выборки.

7.3. Построение гистограммы выборки

Гистограмму выборки строим по следующему алгоритму.

1. Экспериментальным путем определяем значения всех элементов исследуемой выборки, например, значений резисторов R_i одной серии. В результате эксперимента записываем вся совокупность значений (в произвольном порядке): {X₁, X₂, …, X_i, …, X_n}.

2. Производим построение вариационного ряда по экспериментальным данным.

Вариационным рядом называется набор значений Z₁, Z₂, …, Z_N, который получаем с учетом исходных данных X_i путем расположения их в порядке возрастания от X_min до X_max. Таким образом, выполняется условие

X_min   Z₁, …   …  Z_n = X_max. (7.2)

Заметим, что наиболее удобно обрабатывать вариационный ряд в системе EXCEL.

Гистограмма выборки представляет собой график зависимости вероятности обнаружения в выборке того или иного значения параметра (сопротивления резистора, емкости конденсатора).

Гистограмму выборки (например, сопротивления резисторов) строим следующим образом:

а) на графике обозначаем оси: Х – исследуемый параметр, например, R, кОм; Y – частота попадания (N_m/N) в тот или иной интервал значений.

Масштаб на осях зависит от экспериментальных значений, например, X_i, от R  R_min до R  R_max;

б) интервал значений (примерно) от R_min до R_max на оси X разбиваем на определенное количество интервалов K, которое находим по оценочной формуле

K = 1 + 3,2lnn. (7.3)

где найденное значение K округляют до ближайшего целого числа.

в) определяем длину интервала на оси ΔX_инт:

ΔX_инт = (X_max  X_min)/K, (7.4)

где ΔX_инт также округляем для удобства вычислений;

в) точку, соответствующую середине области изменения выборки (центр распределения) (X_max + X_min)/2, принимаем за "центр" выборки и центр некоторого интервала, после чего находим границы и окончательное количество (значение K может быть скорректировано) интервалов, так, чтобы они в совокупности перекрывали всю область от X_min до X_max (на оси Х желательно отметить начало и конец каждого интервала);

г) проводим анализ построенного вариационного ряда.

Подсчитываем число N_m экспериментальных значений, например, сопротивлений, попавших в каждый интервал между Х_m и (X_m + ΔX_инт), причем N_m равно числу членов вариационного ряда, для которых справедливо неравенство

X_m  Z_i   Х_m + ΔX_инт,

где Х_m и (X_m + ΔX_инт) – границы m-интервала.

Отметим, что значения Z_i, попавшие на границу между (m-1) и m-интервалами, относят к m-интервалу;

д) подсчитываем относительное количество (относительную частоту или количество процентов) наблюдений f_m = N_m/N, попавших в m-й интервал. Значение f_маx частоты определяет масштаб оси Y (рис. 7.2).

Например, если при N = 100, в первый (от минимального значения) интервал попало 3 значения, то значение f₁ = 3 / 100 = 0,03 или 3 %.

Рис. 7.2

е) строим гистограмму, представляющую собой ступенчатую кривую, значение которой на m-интервале равно f_m (рис. 7.2);

ж) через верхние значения "ступеней" проводим плавную линию, которая завершает построение гистограммы.

При малых значениях N кривая f_m(X) (рис. 7.2) может значительно отличаться от теоретической зависимости (7.1). Максимальному значению f_max соответствует наиболее вероятное значение Х_вер в данной выборке. При увеличении значения n гистограмма переходит в плавную кривую f(X), которая описывается зависимостью (7.1) кривой Гаусса (рис. 7.1).

Границы X, соответствующие значению среднего квадратического отклонения σ, примерно определяем исходя из условия, что в интервал (X_ср  σ…, X_ср + σ) попадает примерно 68 % всех значений. С учетом этого условия рассчитываем величину σ.

На практике экспериментальное распределение может отличаться от распределения Гаусса в силу различных причин. Значение допуска определяем по соотношению

D  σ·100/Х_ср, %. (7.5)