Лабораторна робота № 55 вивчення резонансу в електричному коливальному контурі

ТЕОРЕТИЧНІ ВІДОМОСТІ

МЕТА РОБОТИ: ознайомитись з явищем резонансу в електричному коливальному контурі, експериментально отримати його резонансні криві та визначити основні параметри контуру.

ПРИЛАДИ: коливальний контур, магазин опорів, міліамперметр, генератор.

Явище резонансу в електричному коливальному контурі має надзвичайно велике практичне значення. Так, сучасний радіозв'язок та телебачення були б неможливими без генераторів i приймачів, де основними елементами є коливальні контури, які працюють в режимі резонансу. Щоб зрозуміти це явище, спочатку розглянемо механізм вільних, а потім вимушених коливань при яких i наступає явище резонансу.

1. Електричний коливальний контур. Вільні незатухаючі коливання

Е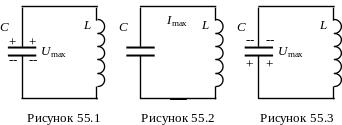 лектричний коливальний контур складається з ємності С (конденсатора) та індуктивності L . В механізмі коливань в такому контурі можна виділити такі основні етапи.

1. Конденсатор заряджений, струм відсутній (рис.55.1). Вся енергія контуру зосереджена в електричному полі конденсатора - формула (55.1), де U_max - максимальне (амплітудне) значення напруги між обкладинками конденсатора.

(55.1)

2. Миттєвій розрядці конденсатора протидіє електрорушійна сила (ЕРС) самоіндукції. Коли струм досягне максимального (амплітудного) значення I_max (рис.55.2), конденсатор буде повністю розряджений і вся енергія контура буде рівна енергії магнітного поля індуктивності L з струмом I_max - формула (55.2).

(55.2)

3. Після того, як струм досягне максимального значення, ЕРС самоіндукції протидіє його зменшенню i ця ЕРС підтримує струм в тому ж напрямі, який i перезаряджає обкладинки конденсатора (рис.55.3), після чого процес розрядки конденсатора починається в зворотньому порядку. Таким чином, в електричному коливальному контурі відбуваються періодичні перетворення енергії електричного поля в енергію магнітного поля і навпаки. Такі перетворення без зовнішньої дії називаються вільними електромагнітними коливаннями. Згідно другого закону Кірхгофа для даного контуру має місце рівняння:

, (55.3)

де - напруга між обкладинками конденсатора при миттєвому значенні заряду q, а весь вираз - ЕРС самоіндукції, яка діє в контурі. Враховуючи, що миттєве значення сили струму дорівнює (55.4), то рівняння (55.3) прийме вигляд (55.5).

, (55.4)

, (55.5)

Розв'язком такого диференціального рівняння є гармонічна функція (55.6), де ₀ - циклічна частота коливань буде рівною (55.7),

q=q_maxsin(₀t+), (55.6)

(55.7)

Так, як , то з (55.7) отримаємо значення періоду власних незатухаючих коливань в електричному коливальному контурі:

. (55.8)

Що стосується максимального (амплітудного) значення заряду q_max конденсатора і ₀ (початкової фази), то ці величини в рівнянні (55.6) визначаються тільки з початкових умов.

2. Вільні затухаючі коливання в контурі

Вільні незатухаючі коливання є ідеальним випадком. В реальних коливальних контурах завжди присутній активний опір, що приводить до затухання коливань, частина енергії контуру перетворюється у внутрішню енергію провідників (провідники нагріваються).

Н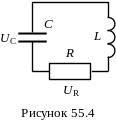 а рис.55.4 наведена схема електричного коливального контуру, в якому резистор R характеризує активний опір всіх ділянок даного контуру. При силі струму I напруга U_R на кінцях резистора буде рівна (55.9) i тоді другий закон Кірхгофа прийме вигляд (55.10) (в лівій частині - сума напруг, в правій сума - ЕРС.)

(55.9)

(55.10)

Розв'язком рівняння (55.10) є функція (55.11),

, (55.11)

де q₀- заряд конденсатора в момент часу t=0, а частота коливань  в даному контурі визначається співвідношенням (55.12).

, (55.12)

Так, як миттєве значення струму знаходиться як перша похідна від заряду за часом (55.4), то взявши таку похідну, отримаємо:

, (55.13)

де добуток q₀ являє собою aмплiтyдне значення сили струму I₀ в момент часу t=0. Тому з рівняння (55.13) випливає, що в коливальному контурі з активним опором амплітуда коливань струму зменшується з часом за законом експоненти, а величину позначають через  i називають коефіцієнтом затухання i тому рівняння (55.13)записують у вигляді (55.14).

, (55.14)

(55.15)

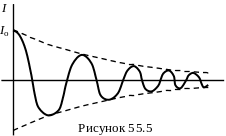
На рис.55.5 наведений графік затухаючих коливань. Для характеристики самого затухання коливань вводять особливу величину (55.15), яку називають логарифмічним декрементом затухання: як логарифм відношення двох послідовних амплітудних значень сили струму (або амплітудних значень заряду чи напруги). Тут логарифм дуже зручна функція. Дійсно, якщо немає затухань, то А_n = А_n+1 i  = ln1 = 0, "нуль" вказує на відсутність затухань коливань.