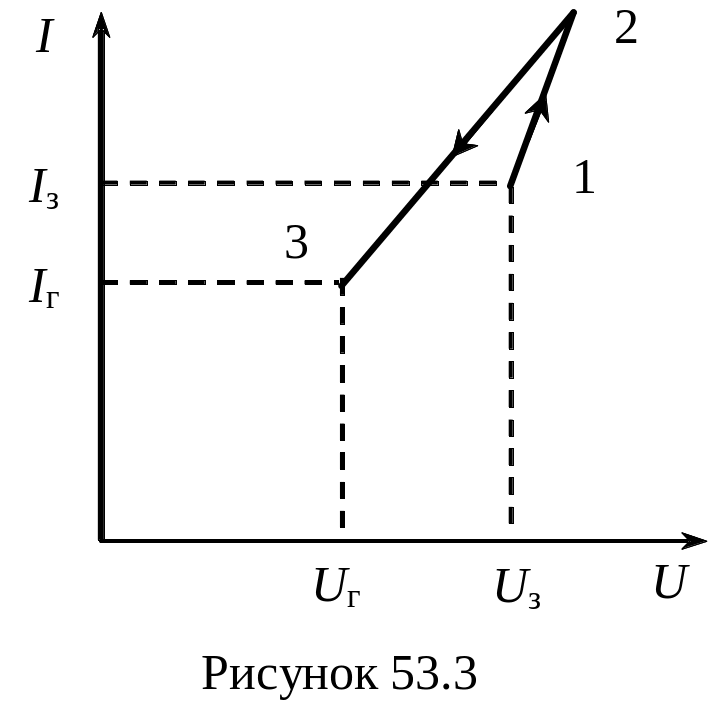
3. Релаксаційний генератор на неоновій лампі.

Неонова лампа - газорозрядний прилад, конструктивно виконаний у вигляді скляного балона заповненого неоном при невеликому тиску (10-15 мм.рт.ст.). В балон впаяні два електрода, розташованих на відстані 1-3 мм. Характерною властивістю неонової лампи є те, що вона починає проводити струм при певному значенню напруги між електродами і ця напруга називається напругою запалювання U_з. При цій напрузі має місце самостійний розряд в неоні у вигляду тліючого розряду. Напруга запалювання залежить від відстані між електродами, їх форми, а також від тиску і природи газу. Після запалювання лампа може світитись при більш низькій напрузі і гасне при напрузі U_г (напруга гасіння). Вольт-амперна характеристика неонової лампи приведена на рис. 53.3. При малих напругах між електродами струм через лампу відсутній, при досягненні напруги запалювання в лампі виникає самостійний розряд і струм стрибком досягає значення I_з (струм запалювання). При подальшому збільшенні напруги (ділянка 1‑2) струм в лампі зростає (явища насичення не розглядаємо).

Якщо зменшувати напругу, то зменшення струму характеризується ділянкою 2-3 (яка близька до ділянки 1-2)

При досягненні напруги U_г, яку називаються напругою гасіння, струм через лампу стрибком спадає до нуля і лампа гасне.

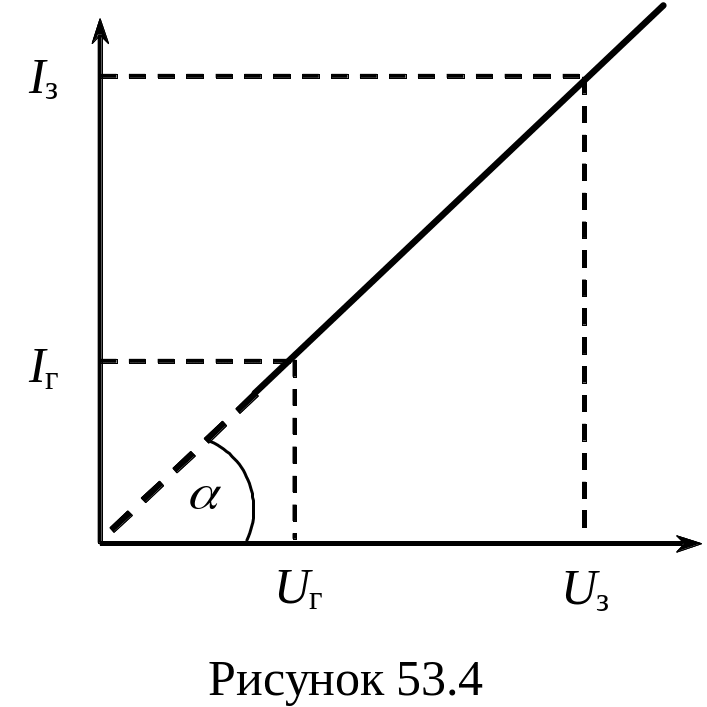
Для спрощеного математичного опису релаксаційного генератора на неоновій лампі користуються ідеалізованою вольт-амперною характеристикою лампи (рис. 53.4), де ділянки 1‑2 та 2‑3 співпадають. У відповідності з цією характеристикою внутрішній опір лампи R_i є розривною функцією від напруги U. Дійсно, при збільшенні напруги від нуля до напруги запалювання U_з опір лампи дорівнює нескінченості R_i =  (струм відсутній). В області значень U > U_з опір лампи має певне кінцеве значення, яке згідно закону Ома дорівнює . Значення цього опору чисельно дорівнює ctg  (рис. 53.4).

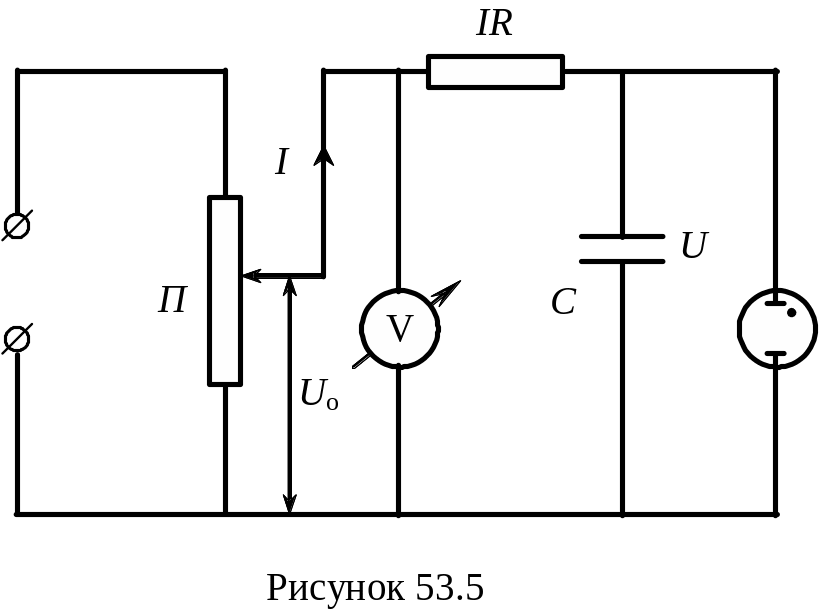Принципова схема релаксаційного генератора на неоновій лампі наведена на рис. 53.5. Паралельно до неонової лампи приєднаний конденсатор ємністю С, який заряджається через резистор опором R від джерела постійного струму. Напруга між обкладинками конденсатора вимірюється вольтметром і регулюється потенціометром П.

При вмиканні кола спочатку відбувається зарядка конденсатора (неонова лампа не горить). Закон зміни напруги на конденсаторі при його зарядці можна знайти, застосовуючи другий закон Кірхгофа для контуру RC.

iR + U =U_o , (53.1)

де iR - напруга на резисторі при значенні струму i, U - напруга на конденсаторі, U_o - напруга джерела струму (напруга на виході потенціометра). Так, як миттєве значення сили струму дорівнює

, (53.2)

а з означення ємності конденсатора - маємо

(53.3)

то отримаємо рівняння

(53.4)

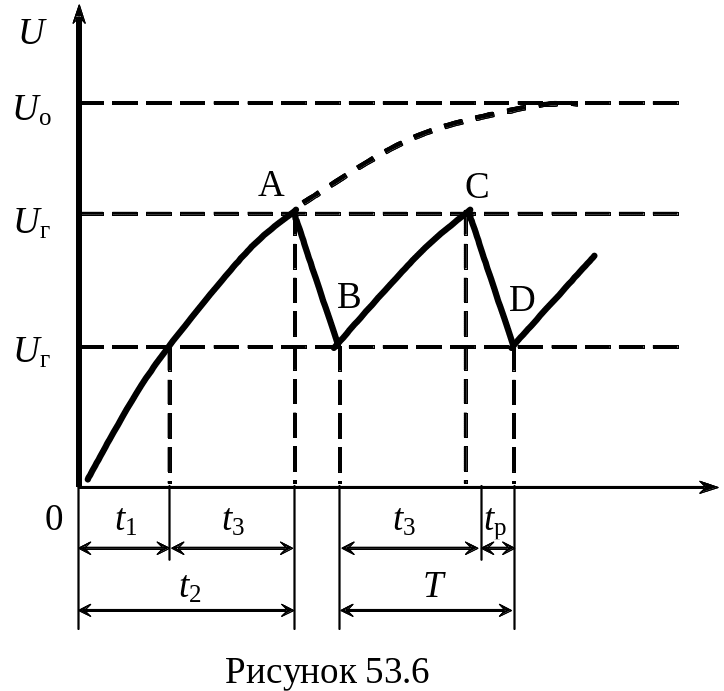
Розв'язком такого рівняння за початкових умов U = 0 при t = 0 буде функція

(53.5)

Як видно з (53.5) напруга на конденсаторі асимптотично наближається до значення U_o (крива ОА, рис.53.6). Але раніше, ніж напруга U досягне значення U_o , лампа загориться. Спалах лампи відбувається при напрузі U = U_з і при цьому її опір стрибком змінюється від R =  до R = const.

Якщо опір R настільки великий, так, що струм, який підводиться від джерела, значно менший розрядного струму через лампу, то конденсатор розряджається (крива АВ). В той момент, коли U стане рівна U_г , лампа гасне і конденсатор знову починає заряджатись. Напруга на ньому зростає по кривій ВС, а потім знову відбувається розрядка (крива CD) і т.д., тобто процес буде періодично повторюватись.

Визначимо період таких релаксаційних коливань. Період Т таких коливань складається з часу зарядки конденсатора t_з та часу його розрядки t_р

Т = t_з + t_р (53.6)

Час зарядки конденсатора , як видно з рис. 53.6, можна визначити через різницю

t_з = t₂ - t₁ (53.7)

де t₂ - час зарядки конденсатора до напруги U_з , t₁ - час зарядки конденсатора до напруги U_г.

В свою чергу значення t₂ і t₁ можна визначити за формулою 53.5

(53.6)

(53.7)

звідки

(53.8)

(53.9)

Тому

(53.10)

Якщо опір резистора R значно більший опору лампи R_і , то час зарядки конденсатора t_з буде значно більший часу розрядки t_р і тому період релаксаційних поливань можна вважати приблизно рівним T= t_з , тобто

(53.11)