Глава 9.
Кореляційно-регресійний аналіз зв’язків
9.1. Основні теоретичні положення
1. Зміст (завдання) кореляційно-регресійного аналізу зв’язків (КРАЗ). Полягає в кількісній оцінці причинно-наслідкових зв’язків між ознаками (результативною та факторними) за допомогою кореляційного та регресійного аналізу.
Завдання КРАЗ:
1) пошук форми рівняння регресії (специфікація моделі) з оцінкою параметрів рівняння (параметризація); перевірка статистичної якості (верифікації) рівняння регресії (2-3):
2) оцінка детермінованості (стохастичності) зв’язку;
3) перевірка значущості оцінок параметрів зв’язку (інтервальна оцінка параметрів) і виконуваності передумов застосування МНК;
4) прогноз.
Перше і друге завдання складають зміст оцінки параметрів, третє – зміст перевірки статистичної гіпотези. Перше завдання побудовано на застосуванні МНК, друге-четверте – на дисперсійному аналізі10.
2. Регресійний аналіз – розділ математичної статистики, що вивчає залежності між випадковими величинами та можливості їх функціонального подання по результатах вибірки; покладений в основу першого завдання КРАЗ.
3. Кореляційний аналіз – метод багатомірного статистичного аналізу для дослідження й оцінки залежностей між випадковими величинами по відповідних коефіцієнтах кореляції; покладений в основу другого завдання КРАЗ.
4. Факторний зв’язок – причинно-наслідковий зв’язок між результативною ознакою Y (залежною змінною) й однією X чи декількома {Xj} (j = 1, 2, …, M) факторними ознаками (пояснювальними змінними, або регресорами), який можна представити аналітично моделлю:
Y = g + E, (9.1)
де g – певна математична функція g(Х) одного X чи декількох {Xj} аргументів – g({Xj}), визначена множиною параметрів {αj}(j = 0, 1, 2, …, M); E – випадковий залишок (випадкова величина) – другорядні фактори.
Види зв’язків:
- кореляційний;
- функціональний;
- невизначений.
У залежності від кількості факторних ознак в моделі зв’язку, факторний зв’язок може бути одно- і багатофакторним.
5. Багатофакторний (однофакторний) зв’язок – зв’язок між однією результативною Y і багатьма факторними {Xj} (j = 1, 2, …, M) ознаками; представляється множинною кореляцією. Якщо факторна ознака одна, такий зв’язок є однофакторним (парна кореляція). Багатофакторний зв’язок представляють рівнянням множинної регресії. Під час застосування КРАЗ воно підлягає якісній перевірці.
Перевірка якості множинної регресії передбачає:
- визначення значущості оцінок коефіцієнтів регресії;
- встановлення загальної якості рівняння регресії;
- аналіз виконуваності передумов застосування МНК.
Загальна якість рівняння множинної регресії перевіряється через:
- встановлення спільної значущості усіх оцінок коефіцієнтів рівняння регресії або оцінюванням множинного коефіцієнта детермінації з перевіркою значущості його оцінки;
- співставлення двох коефіцієнтів детермінації;
- аналіз збіжності рівнянь регресії для двох вибірок.
Однофакторний зв’язок представляють рівнянням парної кореляції (регресії), яке так само проходить перевірку якості через визначення значущості коефіцієнтів регресії та парного коефіцієнта (індексу) детермінації.
6. Кореляційний зв’язок – факторний зв’язок, обумовлений всіма факторами, основним(-и), а також другорядним(-и) (залишком), і який може бути поданий в області визначення змінних моделлю виду Y = g + E, що неоднозначно пов’язує результативну Y та факторну(-і) X ({Xj}, j = 1, 2, …, M) ознаки завдяки невідомому залишку E = EY(X, Y) (E = EY({Xj}, Y)): при одному й тому ж самому значенні факторної ознаки результативна ознака може набувати різних значень. Такий зв’язок ще називають статистичним, або стохастичним, або імовірнісним. Його графічне зображення має назву «кореляційного поля». Вплив кожної j-ої компоненти (Xj-фактора) цього зв’язку на зміну результативної ознаки (говорять, що вони корелюють одна з одною) характеризується відповідним(-и) параметром(-и), а його дослідження уможливлюється завдяки дисперсійному аналізу, як складової КРАЗ. Визначити вид функції g можна лише наближено по результатах n вибіркових спостережень, як функцію, і це складає основу регресійного аналізу.
7. Функціональний зв’язок – факторний зв’язок, обумовлений лише основним(-и) фактором(-и), який може бути поданий в області визначення змінних математичною функцією виду Y = g, що однозначно пов’язує результативну Y та факторну(-і) X ({Xj}, j = 1, 2, …, M) ознаки – g = g(Х) (g = g({Xj})), тобто є повністю визначеним функціонально, або детермінованим.
Функціональний зв’язок є ідеалізованим, застосовується для наближеного представлення кореляційного зв’язку між ознаками функцією виду
YХ = gY(Х) = ğ(Х) або Y{Xj} = gY({Xj}) = ğ({Xj}) (9.2)
і має назву «регресія Y на Х ({Xj})».
Рівняння регресії представляє кореляційний зв’язок без урахування залишку E (невраховані фактори в моделі кореляційного зв’язку), тобто теоретично. Інакше, функція ğ є робочою статистичною гіпотезою – гіпотетично представляє кореляційний зв’язок математичною залежністю результативної ознаки від кожного Xj-фактора, з яким результативна ознака пов’язана певним коефіцієнтом регресії αj, що входить в рівняння регресії у значенні його оцінки аj, обчисленої по вибіркових даних.
Поширеними функціями є такі (в т.ч. однофакторні) (9.3)
а) лінійна – YX1…ХM = а0 + а1X1 + а2X2 + … + аMXM (YX = а0 + а1X);
б) квадратична – YX1…ХM = а0 + а1X1² + а2X2² + … + аMXM²
(YX = а0 + а1X + а2X² – квадратична парабола);
в) кубічна – YX1…ХM = а0 + а1X1³ + а2X2³ + … + аMXM³
(YX = а0 + а1X + а2X3 + а3X³ – кубічна парабола);
г) показникова – YX1…ХM = а0а1X1а2X2…аMXM (YX = а0а1X);
д) напівлогарифмічна – YX1…ХM = а0 + а1lgX1 + а2lgX2 + … + аMlgXM
(YX = а0 + а1lgX).
Задача визначення виду регресії Y на Х ({Xj}) – це задача аналітичного вирівнювання.
8. Специфікація моделі регресії – аналітична форма факторного зв’язку, основу якої складають досліджувані фактори (чинники) і яка має імовірнісний характер, обумовлений стохастичним залишком. Специфікація передбачає добір факторів, які впливають на зміну результативної ознаки Y і включені в рівняння регресії функціонально, як незалежні змінні Xj, кожна зі своїм параметром αj, а також вибір форми зв’язку.
Форма зв’язку і перелік факторів можуть неодноразово уточнюватись для попередження похибок специфікації. Питання про вибір найкращої (адекватної) форми залежності має базуватися на перевірці узгодженості виду функції з первісними даними спостереження. Адекватність побудованої моделі можна встановити з аналізу залишків моделі. Невипадковий характер останніх перевіряється за критерієм Дарбіна-Уотсона. Відбір факторів для побудови багатофакторних моделей здійснюється з використанням статистичних і математичних критеріїв, поширеним серед яких є тристадійний відбір факторів.
9. Похибки специфікації – похибки оцінки параметрів моделі факторного зв’язку, обумовлені неточністю специфікації; можуть бути трьох видів:
- першого роду – ігнорування істотної пояснювальної змінної; призводить до зміщення оцінок, яке буде тим більшим, чим більша кореляція між уведеними та не уведеними до моделі змінними, що в результаті може дати хибний висновок про значущість оцінюваного параметра;
- другого роду – уведення в модель незалежної змінної, яка не є істотною для вимірюваного зв’язку; не дає зміщення оцінки параметра, однак, існує імовірність хибного визнання істотним зв’язку залежної змінної з другорядним фактором;
- третього роду – визнання пояснювальної змінної, яка нелінійно входить в модель зв’язку, за таку, що входить лінійно; наслідки є аналогічними похибці першого роду.
За наявності таких похибок специфікація уточнюється шляхом правильного вибору форми регресії або уведення в модель нової пояснювальної змінної.
10. Регресія11 Y на X – будь-яка функція gY, така, що наближено відбиває статистичну залежність Y від X:
Y = gY + E, – (9.3')
і є найкращою оцінкою ğ = gY випадкової величини Y у розумінні найменших квадратів (МНК)12.
Графічне зображення ğ має назву «регресійна крива», або «лінія регресії».
11. Аналітичне вирівнювання кореляційного зв’язку – розповсюдження властивостей запропонованої функції регресії на характеристики кореляційного зв’язку. Вона зводиться до обчислення невідомих параметрів {αj} (j = 0, 1, 2,…, M) рівняння регресії (одного чи декількох), обраного в якості робочої гіпотези, й відбору адекватного рівняння. Оцінки параметрів визначаються за допомогою методу найменших квадратів.
12. Метод найменших квадратів (МНК) щодо оцінювання параметрів моделі регресії – сума квадратів різниці фактичних (емпіричних) yі значень залежної змінної й її теоретичних yхi значень має бути найменшою:
(9.4)
Імовірнісне обґрунтування методу. Емпіричні значення yi можуть бути представлені як значення незалежних випадкових величин Yi з математичними сподіваннями yхi і середніми квадратичними відхиленнями σi, що характеризують похибку вимірювання. Якщо вважати точність вимірювання незмінною (σi = σ = const), то закон розподілу кожної випадкової величини Yi визначається як нормальний з параметрами (yхi, σ). Отже, ймовірність події Y = {yi} буде максимальною, коли функція правдоподібності L(Y) = L(y1, y2, …, yN) набуває максимального значення (принцип максимальної правдоподібності):
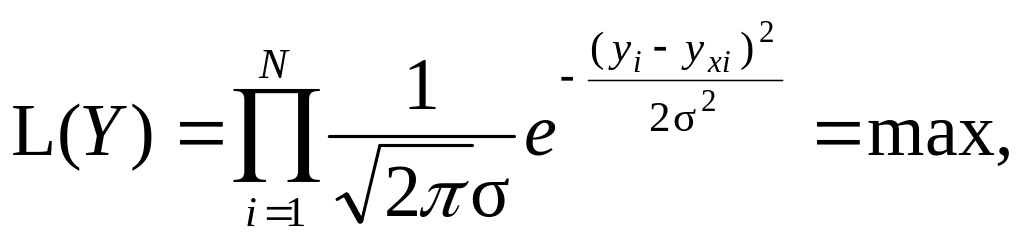(9.5)
або коли
(9.6)
що відповідає вимогам МНК.
Застосування МНК. Якщо теоретичну криву можна представити поліномом степеня M, то визначення оцінок {аj} ( j = 0, 1, …, M) параметрів моделі факторного зв’язку здійснюється відповідно до останнього рівняння шляхом розв’язання системи (M + 1) лінійних рівнянь:
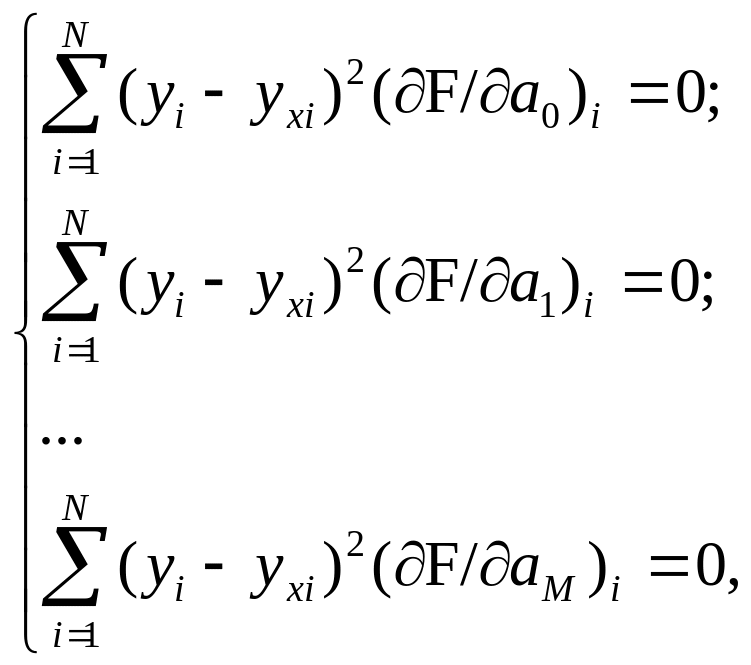(9.7)
де (∂F/∂аj)і – значення частинної похідної функції F по аj в точці хi.
Інакше, в ліву частину тотожності, як в рівняння функції, замість yхi підставляється права частина рівняння моделі регресії, після чого функція диференціюється по невідомих оцінках, а кожна похідна прирівнюється до нуля; отримана в такий спосіб система нормальних рівнянь (їх кількість співпадає з кількістю (M + 1) шуканих оцінок параметрів) розв’язується за допомогою правила Крамера (спосіб визначників) або у спосіб взаємного виключення змінних (методом Гауса). Підстановка значень хi у формулу рівняння регресії дає теоретичні (гіпотетичні) значення yхi результативної ознаки, сума яких повинна бути такою ж самою, як і сума фактичних значень yi: Σyхi ≡ Σyi.
13. Адекватна модель регресії – це така функція ğ, яка у розумінні найменших квадратів (МНК) найкращим чином відображає регресію Y на Х ({Xj}). Відбір адекватної функції здійснюється за допомогою критерію найменшої середньої квадратичної похибки апроксимації: адекватним є те рівняння, для якого дана похибка є найменшою, – тобто адекватна функція мінімізує середній квадрат відхилень
.
(9.8)
14. Середня (відносна або квадратична) похибка апроксимації – це похибка, яка показує, як у середньому відхиляються теоретичні значення yхi результативної ознаки Y від її фактичних значень yi, і може бути визначена за однією з формул:
- середньої відносної похибки апроксимації –
(9.9)
- середньої квадратичної похибки апроксимації –
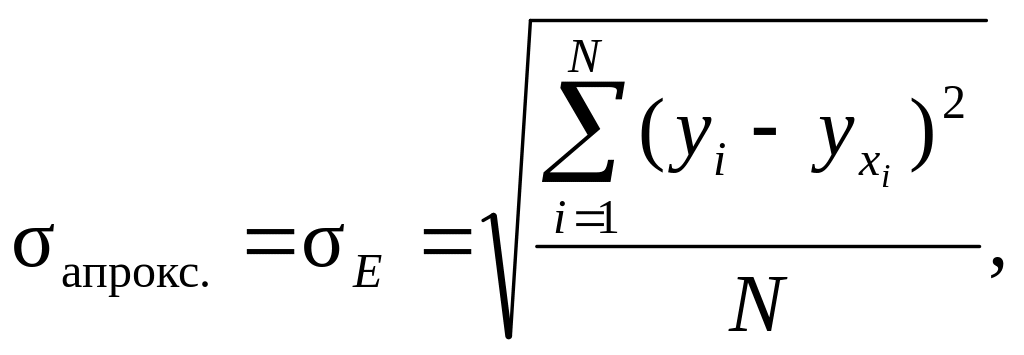(9.10)
де
– значення похибки апроксимації, залишку
E,
який є нормальною випадковою величиною
з параметрами (0, σ).
15. Лінійний зв’язок і лінійна регресія. Багатофакторний зв’язок (множинна кореляція) – зв’язок, який лінійно пов’язує результативну Y ознаку з кожною з факторних ознак Хj рівнянням
(9.11)
де αj – параметри лінійної моделі факторного зв’язку; Х0 – фіктивна змінна – факторна ознака з одиничними значеннями; E – випадковий залишок (другорядні фактори).
Наявність в рівнянні зв’язку випадкового залишку Е дає підстави розглядати зв’язок як множинну кореляцію між залежною змінною Y і множиною пояснювальних змінних {Хj}, а її модель – представляти для зручності в матрично-векторному виді:
Y = αX + E, (9.12)
де Y – вектор-стовпець значень результативної ознаки розміру N; α – вектор-стовпець параметрів факторного зв’язку розміру (M +1); Х – матриця значень факторних ознак Х0, Х1, …, ХM розміру (N × (M + 1)); E – вектор-стовпець значень залишку розміру N.
Тобто
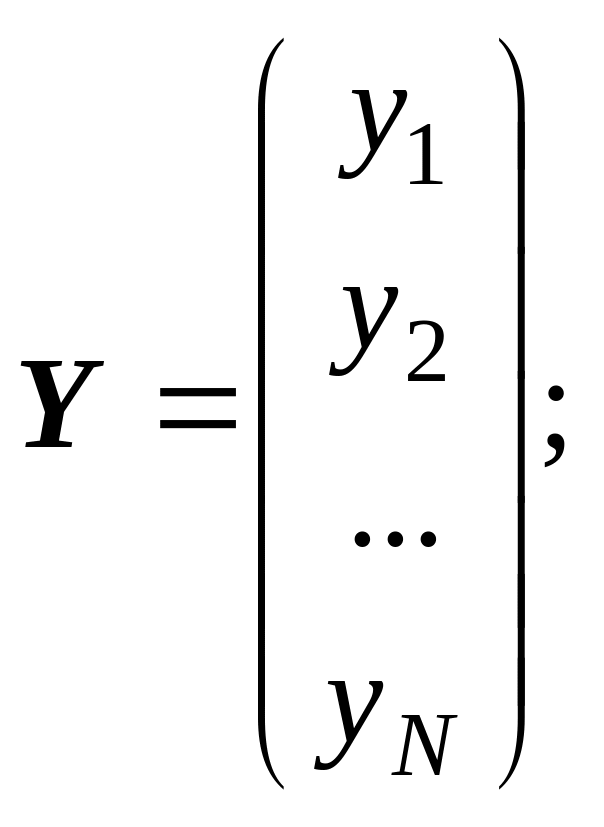
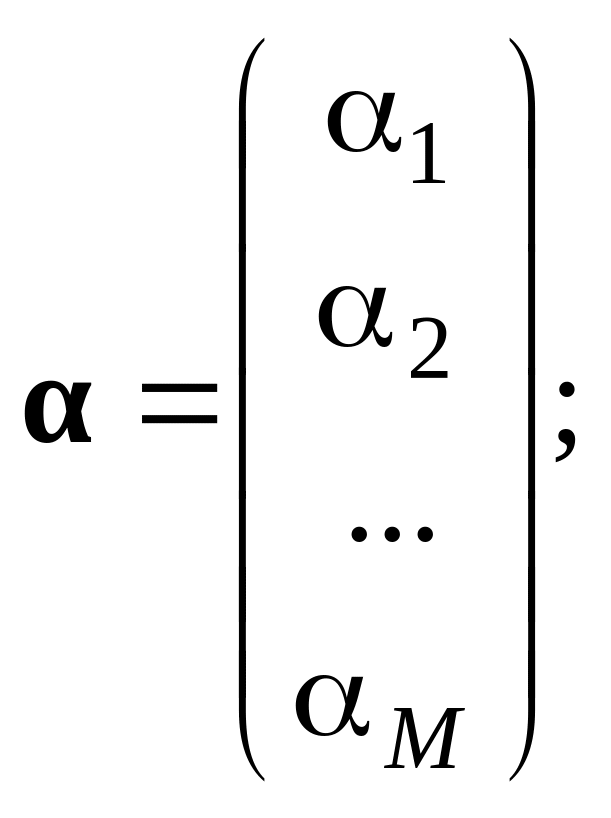
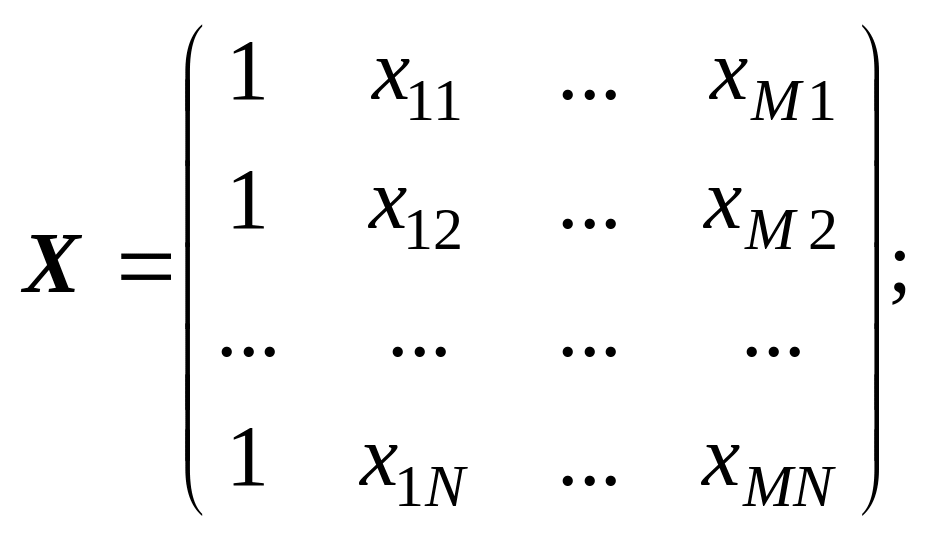
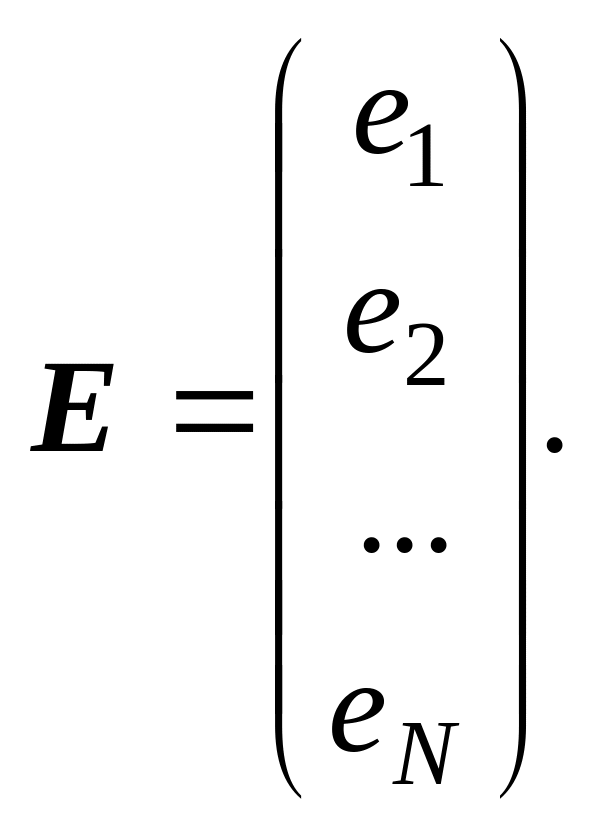(9.13)
Рівняння регресії, що гіпотетично (функціонально та наближено, без урахування E) характеризує багатофакторний зв’язок між Y і {Xj}, представляє множинну регресію та має вид:
YХ = АX, (9.14)
де YХ – вектор-стовпець гіпотетичних значень результативної ознаки розміру N; А – вектор-стовпець оцінок параметрів факторного зв’язку розміру (M + 1);
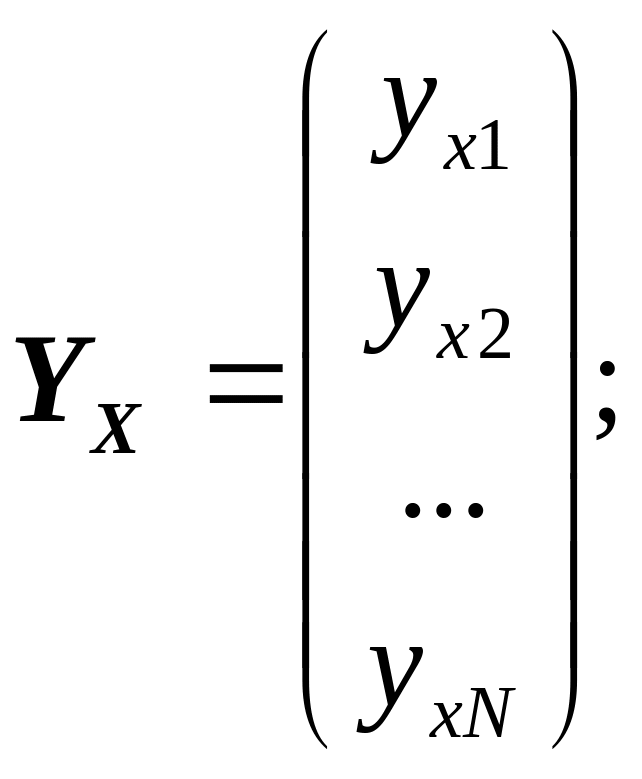
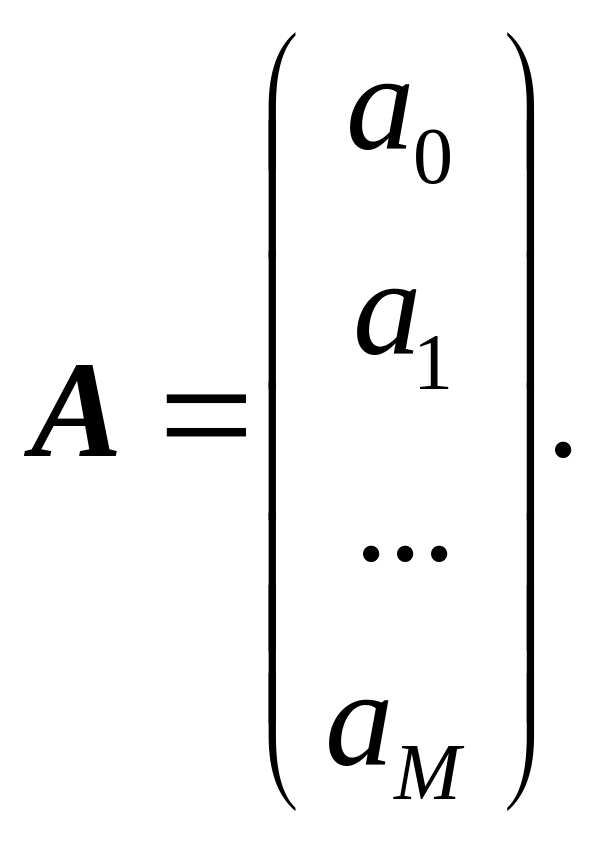(9.15)
Оцінки аj параметрів αj, визначені із застосуванням МНК, мають вид:
А=(X'X)-1X'Y, – (9.16)
де X' – результат транспонування матриці Х; (…)-1 – обертання матриці.
Якщо факторні змінні входять в рівняння регресії нелінійно, його можна привести до лінійного виду переходом до нової змінної, залежність результативної змінної від якої є лінійною.
Однофакторний зв’язок (парна кореляція) – зв’язок, який лінійно пов’язує результативну ознаку Y з однією факторною ознакою Х рівнянням (моделлю парної кореляції)
Y = α0 + α1X + Е. (9.17)
Лінійне рівняння регресії, що гіпотетично (функціонально та наближено) характеризує зв’язок між Y і X як парну регресію: YX = а0 + а1X, – де оцінки а0 і а1 параметрів моделі, визначені із застосуванням МНК і способу визначників (або взаємного виключення змінних), мають вид:
і
,
– (9.18)
і показують відповідно точку перетину прямої лінії регресії з віссю ординат (значення YХ при Х = 0) і швидкість регресії – абсолютну зміну YХ (приріст при а1 > 0 і зменшення при а1 < 0) при зміні Х на одиницю виміру.13
16. Показникова функція регресії (на прикладі однофакторного зв’язку) – функція виду YX = а0а1X, в якій оцінки а0 і а1 параметрів моделі, визначені із застосуванням МНК і способу визначників (або взаємного виключення змінних), мають вид:
і
,
–
(9.19)
і показують відповідно точку перетину прямої лінії регресії з віссю ординат (значення YХ при Х = 0) й інтенсивність регресії – відносну зміну YХ (зростання при а1 > 1 і зменшення при а1 < 1) при зміні Х на одиницю виміру.
17. Напівлогарифмічна функція регресії (на прикладі однофакторного зв’язку) – функція виду YX = а0 + а1lgX, в якій оцінки а0 і а1 параметрів моделі, визначені із застосуванням МНК і способу визначників (або взаємного виключення змінних), мають вид:
і
,
– (9.20)
і показують відповідно значення YХ при Х = 0 й інтенсивність регресії – відносну зміну YХ (зростання при а1 > 0 і зменшення при а1 < 0) при зміні Х на одиницю виміру.
18. Передумови застосування МНК.
Перша передумова. Математичне сподівання залишків дорівнює нулю:
М(E) = 0. (9.21)
У протилежному випадку існує систематичний вплив на результативну ознаку з боку не уведених в модель інших основних факторів.
Наслідок – поява помилок специфікації першого роду. Методом запобігання останніх є покрокова регресія.
Друга передумова. Значення еі вектора залишків E незалежні між собою (відсутня кореляція між ними) і¸ до того ж, мають сталу дисперсію (гомоскедастичність):
(9.22)
У протилежному випадку:
- по-перше, коли виникає автокореляція залишків, M(EE') = σE²S, де S – матриця розміру (N × N), яка характеризує коваріацію між залишками при сталій їх дисперсії σE²;
- по-друге, дисперсія залишків змінюється для кожного спостереження або групи спостережень, тобто M(EE') = σE²S, де S – симетрична додатно визначена матриця, і має місце гетероскедастичність.
Третя умова. Пояснювальні змінні моделі не пов’язані із залишками:
М(X'E) = 0. (9.23)
У протилежному випадку має місце кореляція основних і другорядних факторів, коли ефект від впливу останніх на результативну ознаку виявляється не одразу, а поступово, через деякий період часу, із запізненням (лагом) τ, і застосовуються моделі розподіленого лагу14, або коли наявність прямих і зворотних зв’язків між результативною і факторною(-и) ознаками вимагає в моделюванні використання системи одночасних структурних рівнянь15.
Наслідок – зростання помилок оцінювання параметрів моделі. Оцінювання параметрів розподіленого лагу здійснюється методами Л.Койка, Ширлі Алмона, часткового коригування й адаптивних сподівань, МНК, Ейткена, ітеративним методом, методом інструментальних змінних, алгоритмом Уолісса.
Оцінювання параметрів системи одночасних структурних рівнянь здійснюється методами МНК, непрямим МНК, дво- і трикроковим МНК (2МНК і 3МНК).
Четверта умова (є специфічною для множинної регресії). Пояснювальні змінні моделі утворюють систему лінійно незалежних векторів (не повинні бути мультиколінеарними):
|Х'Х| = 0. (9.24)
У протилежному випадку, якщо застосовуватиме малі скінчені сукупності спостережень, за наявності вираженої тенденції зміни пояснювальних змінних у часі, або за наявності лагових змінних, |Х'Х| ≠ 0 (матриця Х має повний ранг), існує мультиколінеарність, і це систематично впливає на результативну ознаку.
19. Детермінованість і стохастичність зв’язку. Детермінованість зв’язку – це визначеність зв’язку між результативною Y і основною факторною (основними факторними) X ({Xj}, j = 1, 2, …, M) ознаками (змінними) функцією виду ğ(X) (ğ({Xj})). Якщо зв’язок між ними неоднозначний, він є стохастичним і обумовлений впливом на результативну ознаку, крім основних факторних ознак, другорядних факторів, які представлені в моделі факторного зв’язку випадковим залишком E.
Міра впливу кожної компоненти факторного зв’язку на Y підлягає якісній і кількісній оцінці. Така оцінка здійснюється через відповідні індекси детермінації та коефіцієнти кореляції, визначення яких є одним з декількох кроків перевірки якості рівняння регресії.
20. Індекс (коефіцієнт) детермінації (R²) – статистичний показник міри детермінованості зв’язку (тісноти зв’язку) між ознаками (змінними), який визначається для перевірки якості регресії, показує частку (відсоток) варіації залежної змінної Y, обумовлену впливом однієї Х пояснювальної змінної (парний індекс детермінації) або сукупним впливом множини {Xj} (множинний індекс детермінації) пояснювальних змінних (впливом регресії) і обчислюється як відношення факторної і загальної дисперсій:
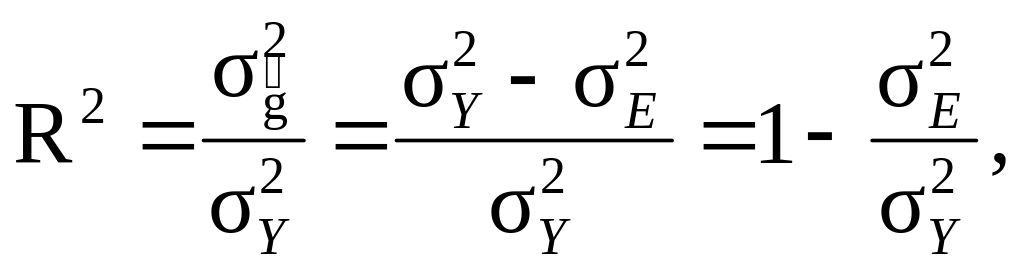(9.25)
де відповідно факторна, загальна і залишкова дисперсії.
Відношення
показує частку (відсоток) варіації
залежної змінної Y,
обумовлену впливом залишку Е.
Факторна
дисперсія
– середня міра квадратичного відхилення
гіпотетичних значень ğ залежної змінної
Y
від середнього арифметичного значення
останньої
:
–
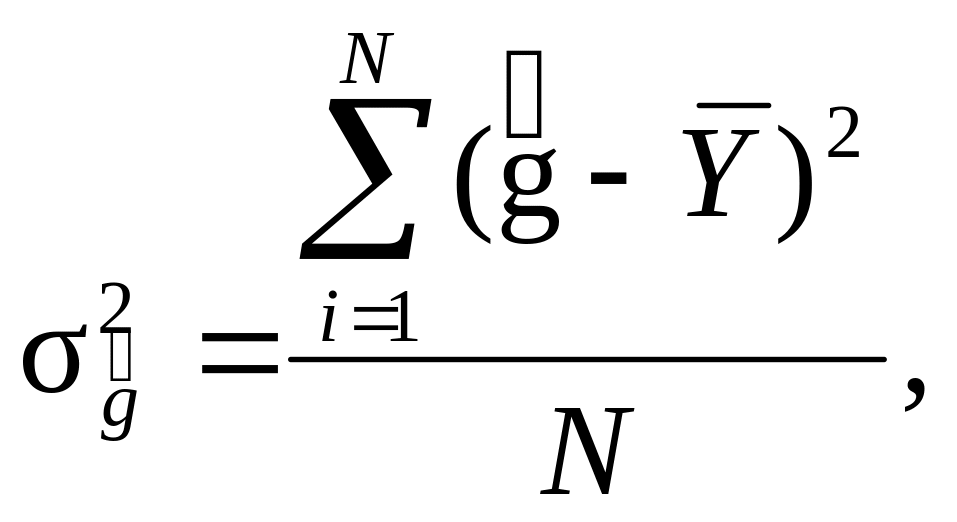(9.26)
обумовлена дією лише пояснювальної змінної (пояснювальних змінних) Х ({Xj}), тобто регресією.
Загальна
дисперсія
–
середня міра квадратичного відхилення
фактичних значень yi
залежної змінної Y
від середнього арифметичного значення
останньої
:
–
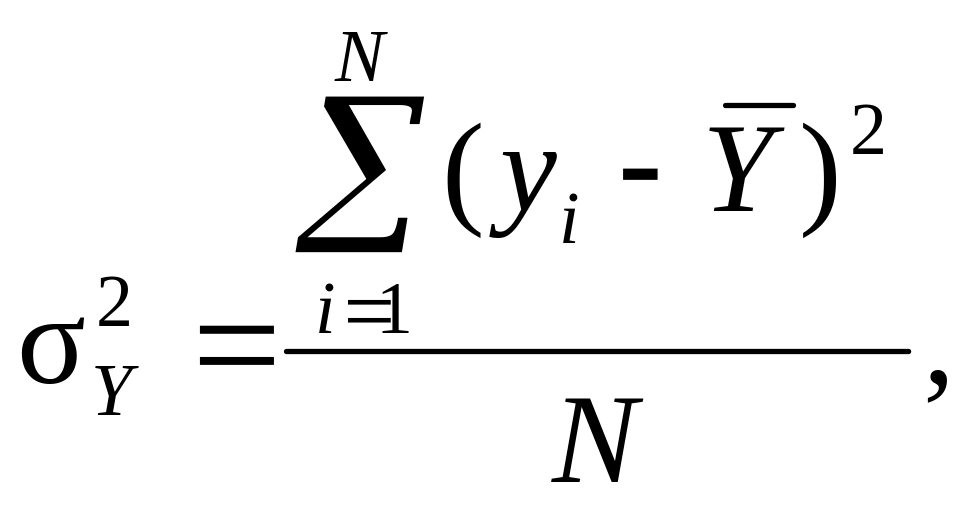(9.27)
обумовлена сукупною дією пояснювальної змінної (пояснювальних змінних) Х ({Xj}) і випадкового залишку E, тобто регресією і залишком.
Залишкова
дисперсія
–
середня міра квадратичного відхилення
гіпотетичних значень ğ залежної змінної
Y
від її фактичних значень
yi:
–
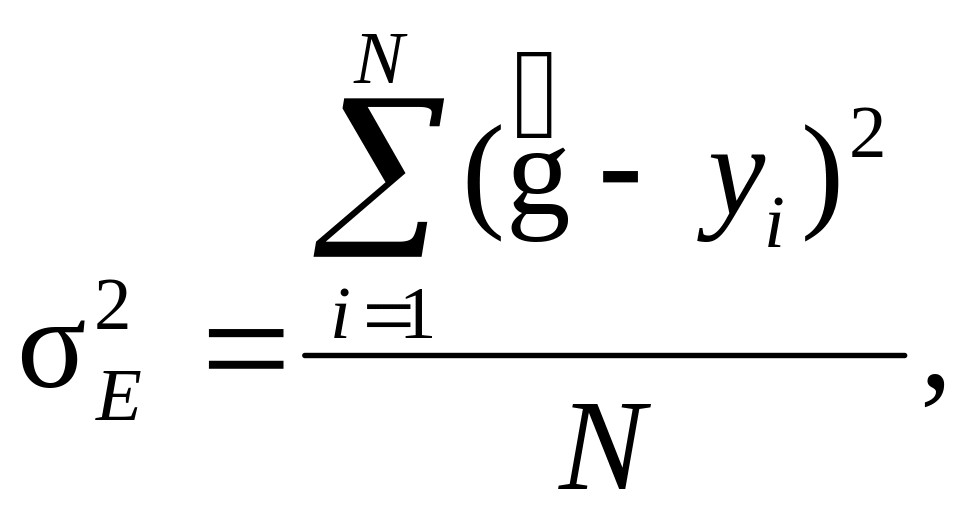(9.28)
обумовлена дією випадкового залишку E, тобто похибками специфікації моделі; є різницею загальної та залишкової дисперсій (витікає з адитивності моделі).
Ці три дисперсії пов’язані між собою правилом «додавання дисперсій».
R² завжди більший за 0 і менший за 1, якщо Y не повністю визначається Х-фактором(-ами), а на нього впливає ще й залишок E, і зв’язок є стохастичним; R² = 0, якщо Y не залежить від Х-фактора(-ів) і обумовлений лише залишком E (зв’язок неви-
значений); R² = 1, якщо Y повністю визначається Х-фактором(-ами) (зв’язок між Y і Х є функціональним). Утворюючи специфікацію моделі, бажано досягти найбільшого значення R², ближчого до одиниці.
Знаючи R², можна якісно оцінити тісноту зв’язку за шкалою Чеддока:
R |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
≥0,9 |
Зв’язок (сила) |
Слабкий |
Помірний |
Помітний |
Сильний |
Дуже сильний |
21. Правило «додавання дисперсій»: загальна дисперсія дорівнює сумі факторної і залишкової дисперсій:
(9.29)
Правило пояснює адитивний вплив на варіацію результативної ознаки Y з боку Х-фактора(-ів) і випадкового залишку E.
22.
Множинний
індекс детермінації
(
)
– статистичний показник, який визначається
для перевірки загальної якості рівняння
регресії й оцінює тісноту факторного
зв’язку між результативною Y
і множиною факторних {Xj}
(j =
1, 2, …, M;
M – натуральне
число, більше за 1) ознак (змінних),
представленого функціонально рівнянням
регресії Y
на {Xj}:
Y{Xj}
=
gY({Xj}),
– як співвідношення факторної та
загальної дисперсій (в т.ч. в матричній
формі):
(9.30)
де
(9.31)
і
(9.32)
–
(9.33)
відповідно факторна, загальна і залишкова дисперсії; λ11 – перший елемент головної діагоналі коваріаційної матриці λ, який є дисперсією σY² залежної змінної Y; Λ11 – перший елемент головної діагоналі матриці Λ, оберненої до матриці λ (Λ = λ-1), який обернено пропорційно пов’язаний із залишковою дисперсією – σE² = 1/Λ11.
Інша матрична форма цього показника має вид:
–
(9.34)
де rYX – вектор-рядок розміру M парних коефіцієнтів взаємної кореляції залежної та пояснювальних змінних (елементів першого рядка кореляційної матриці, крім першого в головній діагоналі); rХX-1 – обернена матриця розміру (M × M) коефіцієнтів взаємної кореляції й автокореляції пояснювальних змінних; r'YX – вектор-стовпець розміру M парних коефіцієнтів взаємної кореляції залежної та пояснювальних змінних (елементів першого стовпця кореляційної матриці, крім першого в головній діагоналі).
Крім того, множинний індекс детермінації може бути визначений в такий спосіб:
(9.35)
де
–
(9.36)
j-ий
нормований коефіцієнт регресії при
пояснювальній змінній Xj,
–
парний коефіцієнт кореляції залежної
Y
і пояснювальної Xj
змінних.
Значення
множинного індексу детермінації
,
отримане по зміщених оцінках залишкової
і загальної вибіркових дисперсій,
і
,
уточнюється (
)
в значеннях незміщених оцінок останніх
–
і
:
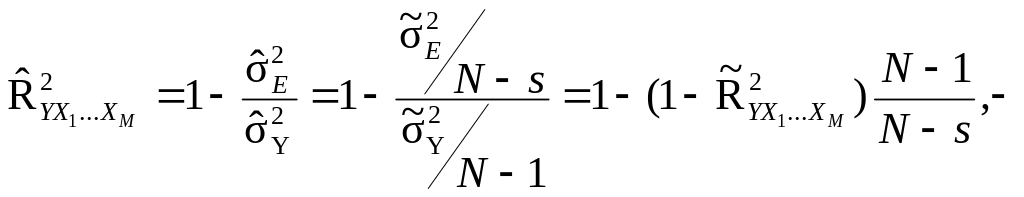(9.37)
з
подальшою перевіркою
на
значущість.
Доведено, що зростає з добавлянням в рівняння регресії кожної чергової пояснювальної змінної тоді й тільки тоді, коли t-статистика для цієї змінної по модулю більша за одиницю. Нові пояснювальні змінні добавляються в рівняння до тих пір, поки зростає індекс детермінації.
23. Коваріація (коваріаційний момент) – коваріація змінних (випадкових величин) Y і Х, або їх коваріаційний (кореляційний) момент – центральний момент другого порядку виду:
.
(9.38)
24. Коваріаційна матриця (λ) (дисперсійний аналіз) – квадратична матриця розміру ((M + 1) × (M + 1))
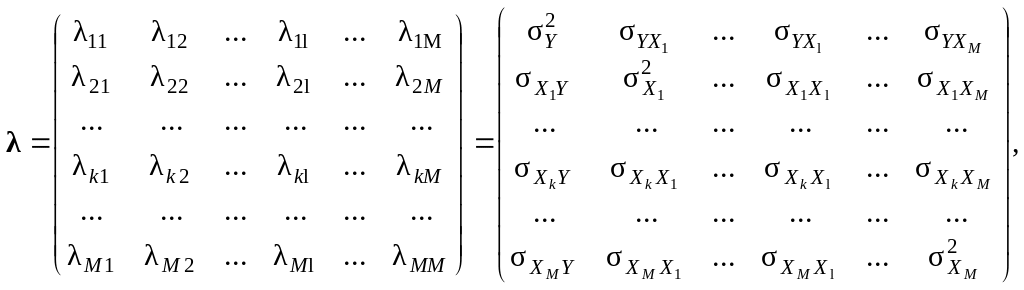(9.39)
елементи
якої λij
(i
= 1, 2, …, M
+ 1, j
= 1, 2, …, M
+ 1) відбивають
попарну коваріацію
залежної
змінної Y
з кожною окремою пояснювальною Xj
(j =
1, 2, …, M)
змінною або коваріацію
пояснювальних
змінних між собою, якщо i
≠ j,
або є дисперсіями
і
цих
змінних, якщо i
= j,
тобто вони є елементами головної
діагоналі матриці:
(9.40)
25.
Парний індекс
детермінації
(RYX²)
– статистичний показник, який оцінює
тісноту факторного зв’язку між
результативною ознакою Y
і однією факторною ознакою
X, який можна
представити функціонально рівнянням
регресії Y
на X:
–
як відношення факторної та загальної
дисперсій:
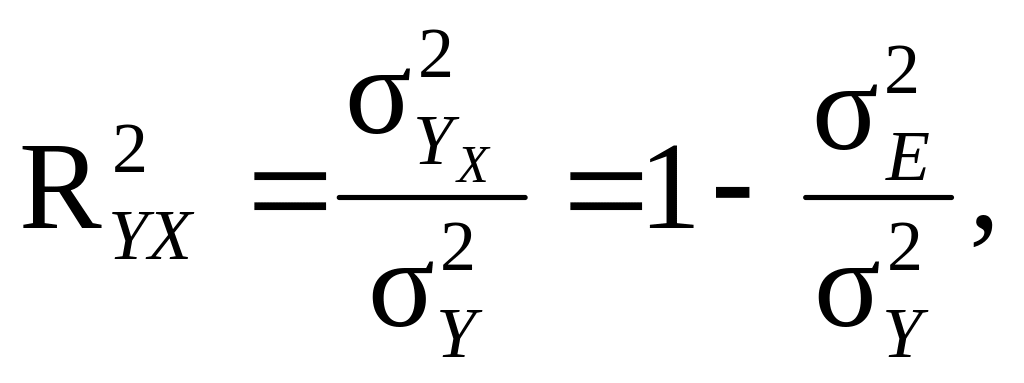(9.41)
де
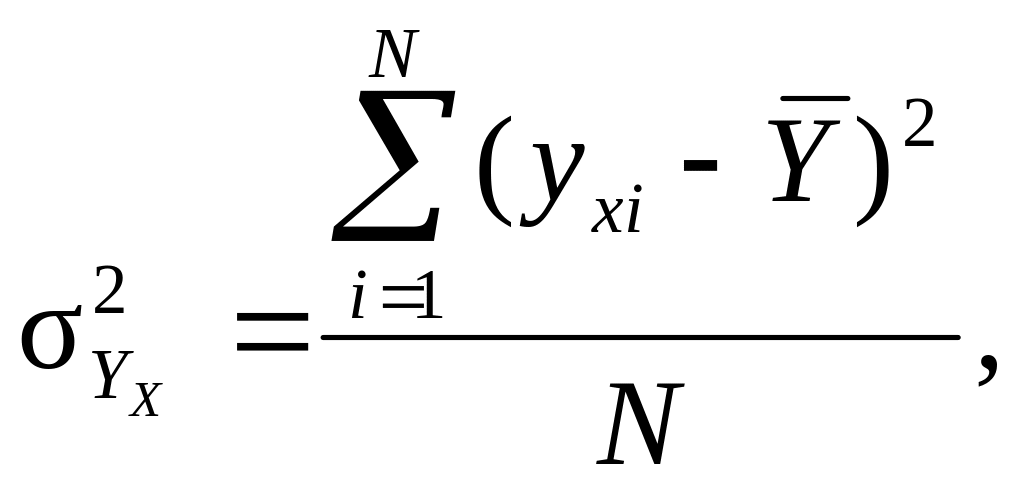(9.42)
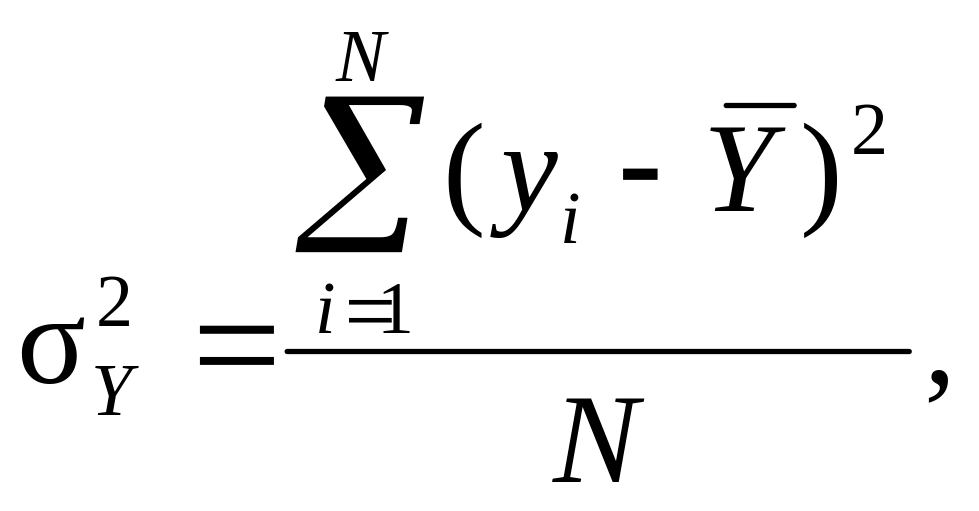(9.43)
–
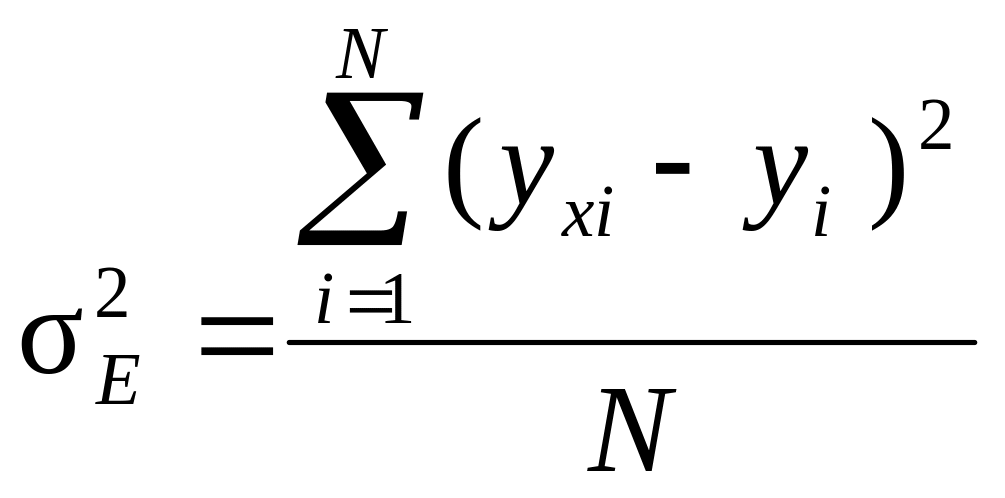(9.44)
відповідно факторна, загальна і залишкова дисперсії.
Для
отримання незміщених оцінок
і
загальної
і залишкової вибіркових дисперсій
останні необхідно помножити на коригуючи
коефіцієнти N/(N
– 1) і N/(N
– 2) відповідно
(N
– об’єм вибірки). Парний індекс
детермінації Y
і Xk-фактора
з множини факторів {Xj}
(j =
1, 2, …, M),
якщо j =
k,
має місце за умов утворення нового
рівняння регресії однофакторного
зв’язку:
,
– з новими оцінками параметрів, які
визначаються по наведених вище формулах
і відрізняються від аналогічних оцінок,
що пов’язують ці ж самі змінні в рівнянні
регресії багатофакторного зв’язку.
На відміну від парного, існує частинний індекс детермінації.
26.
Частинний
індекс детермінації
(
)
– статистичний показник, який оцінює
тісноту зв’язку між результативною
ознакою Y
і будь-яким Xk-фактором
при елімінації
решти пояснювальних змінних {X1,
…, Xk-1,
Xk+1,
…, XM}:
.
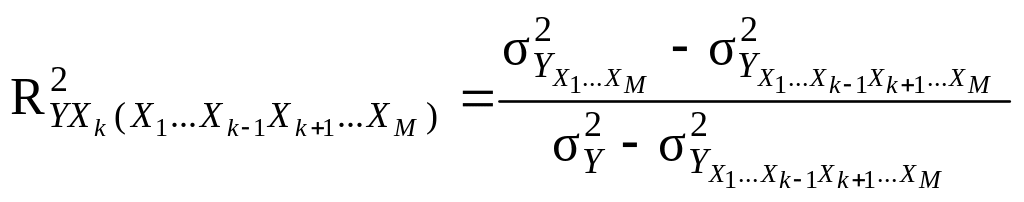(9.45)
Елімінація факторів – виключення з рівняння регресії багатофакторного зв’язку складових відповідних факторів, не змінюючи оцінки параметрів при факторах, що залишаються в рівнянні. У розглянутому прикладі в рівнянні залишається Xk-фактор, решту змінних, {X1, …, Xk-1, Xk+1, …, XM}, виключено з рівняння (у формулі зображено дужками).
Аналогічно можна оцінити тісноту зв’язку між двома будь-якими факторними ознаками Xk і Xl .
27. Коефіцієнт кореляції (r) – статистичний показник міри лінійного статистичного зв’язку змінних між собою (взаємна кореляція). Такий зв’язок має місце за умов впливу на залежну змінну Y, крім Х-фактора (-ів), випадкового залишку E, який є різницею між цією змінною й її лінійною оцінкою –
(9.46)
Якщо змінних дві, їх кореляція є парною (M = 1, M – натуральне число); якщо зв’язок обумовлений множиною пояснювальних змінних (M > 1), кореляція є множинною.
Інакше, коефіцієнт кореляції вимірює якість «найкращого» лінійного наближення gY({Xj}) функції g({Xj}) факторного зв’язку, мінімізуючи залишкову дисперсію σE² так, що σE² = σY²(1 – r²). Тоді коефіцієнт кореляції можна оцінити через загальну σY², залишкову σE² і факторну σgY² дисперсії (рівність має назву «кореляційне відношення»16):
(9.47)
або як корінь квадратний з коефіцієнта детермінації:
(9.48)
|r| завжди більший за 0 і менший за 1, якщо між Y і Х-фактором(-ами) існує кореляційний зв’язок (r > 0, якщо при зростанні (зменшенні) Х зростає (зменшується) Y – додатна кореляція; r < 0, якщо при зростанні (зменшенні) Х зменшується (зростає) Y – від’ємна кореляція); r = 0, якщо Y лінійно не залежить від Х-фактора(-ів) (Y і Х некорельовані); |r| = 1, якщо Y лінійно залежить від Х-фактора(-ів) (необхідна та достатня умова лінійної залежності між ними).
28.
Множинний
(зведений)
коефіцієнт
кореляції
(
)
– статистичний показник, який оцінює
міру лінійного статистичного зв’язку
між результативною Y
і множиною факторних {Xj}
(j =
1, 2, …, M)
ознак (змінних), який можна представити
рівнянням
де
–
(9.49)
лінійна регресія Y на {Хj}, а E – випадкова величина – залишок Y відносно пояснювальних змінних {Хj}, M – натуральне число, більше за 1.
Інакше, він оцінює зведену коваріацію (кореляцію) змінних Y і {Хj} (є мірою кореляції між ними) і може бути представлений рівнянням (в т.ч. в матричній формі):
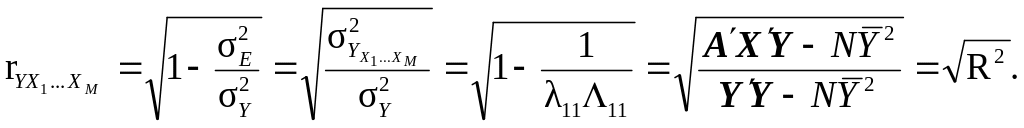(9.50)
Інша матрична форма цього показника має вид:
(9.51)
де rYX і rXX – відповідно парні коефіцієнти взаємної кореляції залежної змінної Y з кожною пояснювальною змінною Хj окремо і парні коефіцієнти кореляції пояснювальних змінних Хj між собою. Усі вони разом входять в кореляційну матрицю r.
Крім того, множинний коефіцієнт кореляції може бути визначений в такий спосіб:
(9.52)
де |r| – визначник кореляційної матриці r, A11 – алгебраїчне доповнення до елемента r11= rYY кореляційної матриці (визначник матриці rXX). Значущість множинного коефіцієнта кореляції перевіряється за t-критерієм.
29. Парний коефіцієнт кореляції (rYX (rХX)) – статистичний показник, який оцінює міру лінійного статистичного зв’язку між двома ознаками (змінними) і є нормованою формою коваріаційного моменту. У факторному зв’язку оцінюють кореляцію таких двох змінних:
1)
результативної
ознаки Y і однієї факторної ознаки X
однофакторного зв’язку,
зв’язок яких можна представити рівнянням
де
–
лінійна
регресія Y
на Х,
а E
– випадкова величина – залишок
Y
відносно пояснювальної змінної Х.
Інакше, він оцінює парну коваріацію (кореляцію) змінних Y і Х (є мірою кореляції між ними) і може бути представлений рівнянням
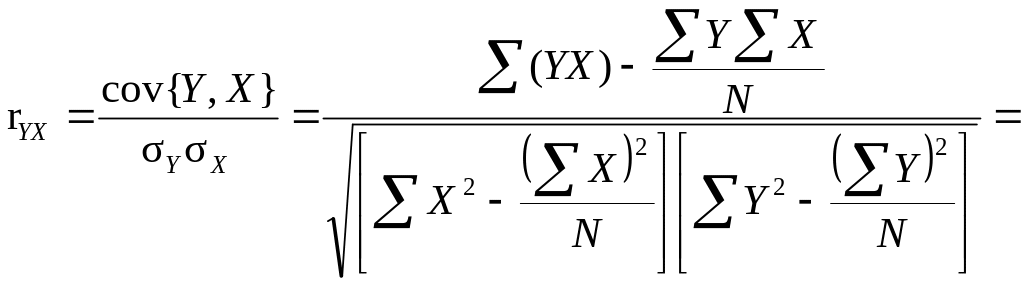
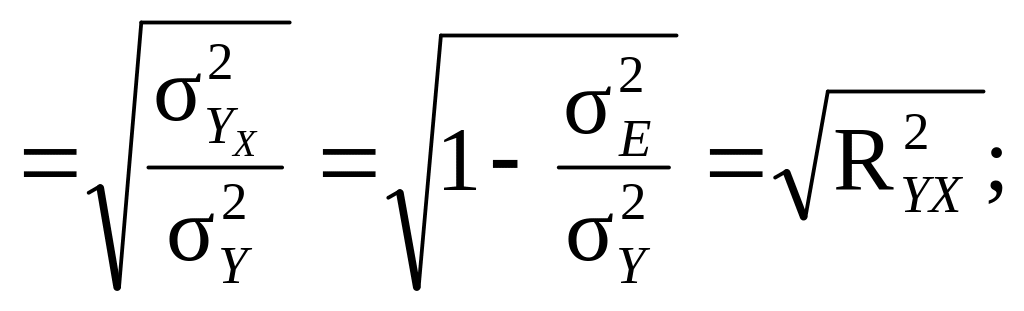(9.53)
2)
результативної
ознаки Y і будь-якої однієї j-ої факторної
ознаки з множини пояснювальних змінних
{Xj}
(j
=1, 2, …,
M)
багатофакторного зв’язку,
,
зв’язок
яких можна
представити відповідним рівнянням у
значеннях Y
і Xj.
Інакше, він оцінює парну коваріацію (кореляцію) змінних Y і Xj (є мірою кореляції між ними) і може бути представлений аналогічно і, крім того, як j-ий елемент вектора-рядка розміру M –
,
(9.54)
елементи якого є парними коефіцієнтами взаємної кореляції залежної змінної Y з кожною окремою пояснювальною змінною Xj –
(9.55)
або вектора-стовпця розміру M –
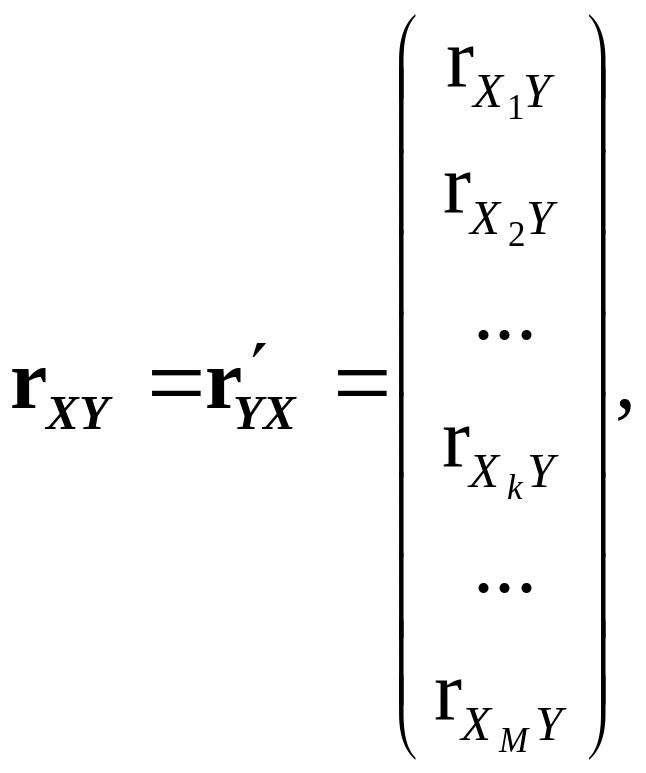(9.56)
елементи
якого є парними коефіцієнтами взаємної
кореляції
кожної окремої пояснювальної змінної
Xj
із залежною змінною Y
–
(9.57)
3)
будь-яких
двох факторних ознак Xk
і Xl
із множини пояснювальних змінних {Xj}
(j
= 1, 2, …,
M)
багатофакторного зв’язку,
,
зв’язок яких можна представити
відповідним рівнянням
у значеннях
Xk
і Xl.
Інакше, він оцінює парну коваріацію (кореляцію) пояснювальних змінних Xk і Xl (є мірою кореляції між ними) і може бути представлений аналогічно і, крім того, як елемент i-го рядка і j-го стовпця матриці розміру (M × M) (i = 1, 2, …, M; j = 1, 2, …, M), якщо i = k, j = l:
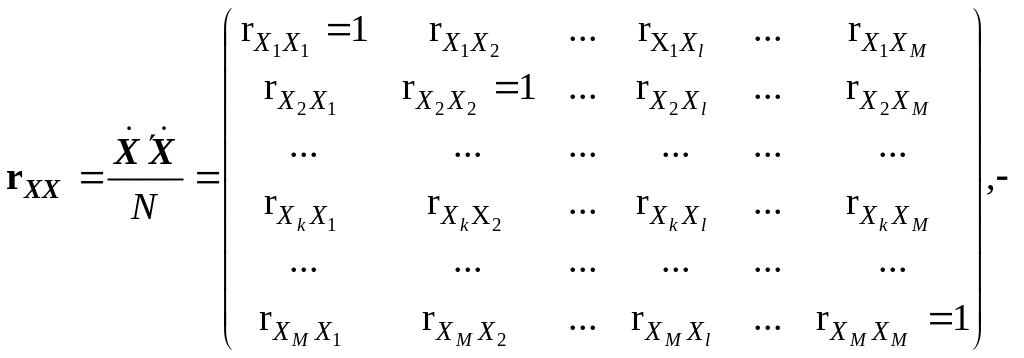(9.58)
елементи
якого є парними коефіцієнтами взаємної
кореляції
пояснювальних
змінних Xi
і Xj,
однієї з іншою –
(9.59)
якщо
i ≠
j,
або є коефіцієнтами автокореляції
пояснювальних змінних (самих із собою),
якщо i =
j,
і які дорівнюють одиниці (елементи
головної діагоналі). Сильна лінійна
залежність між пояснювальними змінними
(
≥
0,7) свідчить про наявність у зв’язку
мультиколінеарності.
Усі ці коефіцієнти утворюють кореляційну матрицю r.
Значущість парного коефіцієнта кореляції перевіряється за t-критерієм. Інші можливі коваріаційні зв’язки, в яких беруть участь залишки, призводять до виникнення похибок специфікації (оцінювання).
На відміну від парного, існує частинний коефіцієнт кореляції.
30. Кореляційна матриця (r) – квадратична матриця розміру ((M + 1) × (M + 1))
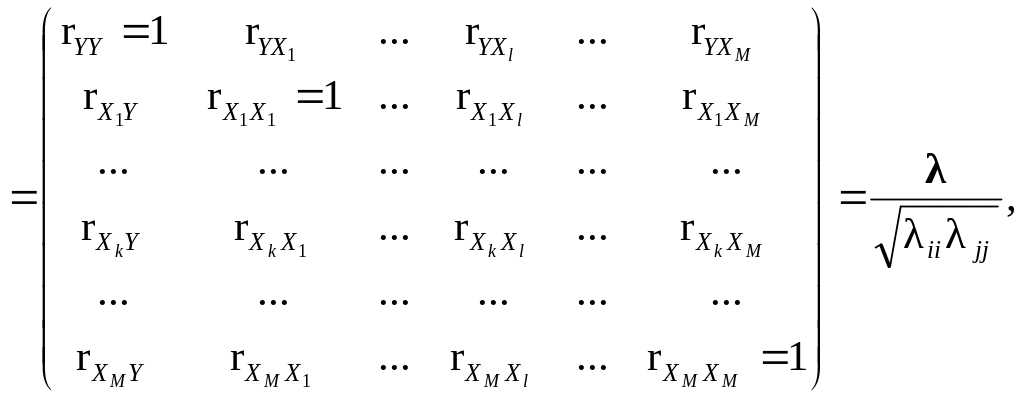(9.60)
елементи
якої rij
(i
= 1, 2, …, M
+ 1, j
= 1, 2, …, M
+ 1) є парними
коефіцієнтами взаємної кореляції
залежної
змінної Y
з кожною пояснювальною змінною Xj
(j =
0, 1, 2, …, M)
окремо або парними коефіцієнтами
взаємної кореляції
пояснювальних
змінних між собою, якщо i
≠ j,
або коефіцієнтами автокореляції
і
цих
змінних (самих на себе), якщо i
= j,
тобто вони є елементами головної
діагоналі цієї матриці, і, до того ж,
мають зв’язок з відповідними елементами
коваріаційної матриці:
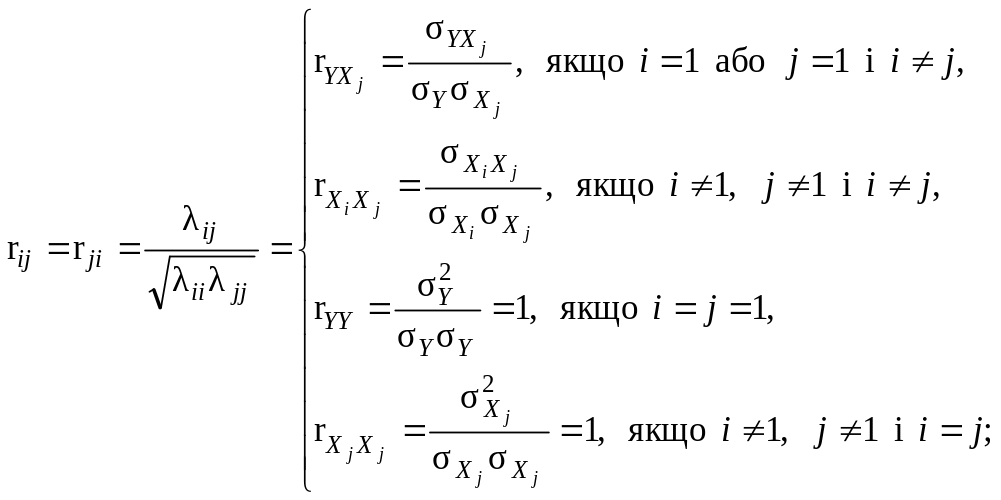(9.61)
–
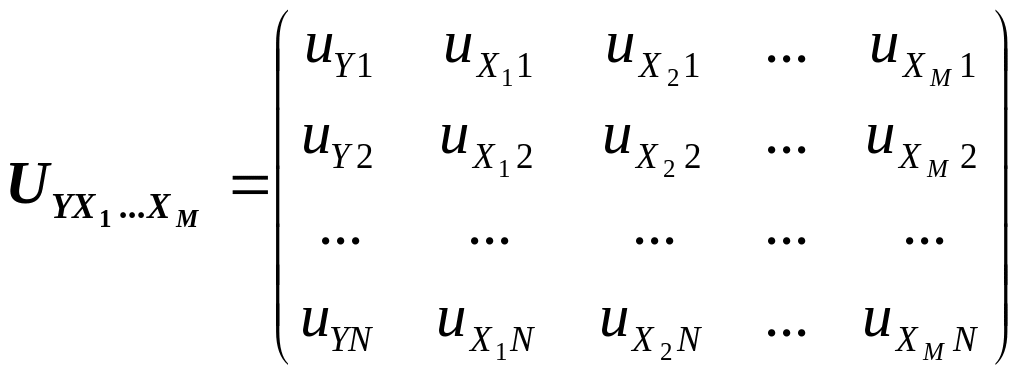(9.62)
це
матриця розміру (N
× (M
+ 1)) нормалізованих
значень
залежної Y
(перший стовпець матриці) і
пояснювальних Xj
(другий,
третій і т.д. стовпці матриці) змінних.
Елементи
матриці r,
крім першого, утворюють:
–
матрицю rXX
розміру (M
× M);
–
вектор-рядок rYX
розміру M;
–
вектор-стовпець rХY
=
rYX'
розміру M.
Визначники
і
відповідних
матриць λ
і r
пов’язані між собою коефіцієнтом
розкиду –
(9.63)
31. Частинний коефіцієнт кореляції (r*) – статистичний показник, який оцінює міру лінійного статистичного зв’язку між двома ознаками при елімінації решти змінних. У факторному зв’язку, зазвичай, оцінюють частинну взаємну кореляцію результативної
ознаки Y і будь-якого Xk-фактора при елімінації решти пояснювальних змінних {X1, …, Xk-1, Xk+1, …, XM}:
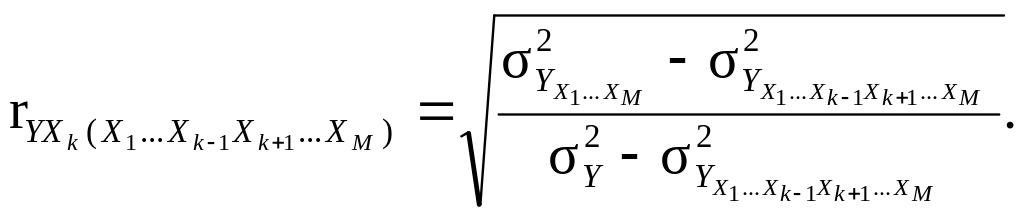(9.64)
Якщо існує залежність між двома будь-якими факторними ознаками Xk і Xl (при наявності мультиколінеарності), то, елімінуючи результативну ознаку і решту пояснювальних змінних, стає можливим визначення частинного коефіцієнта взаємної кореляції Xk і Xl факторів.
Усі частинні коефіцієнти разом утворюють кореляційну матрицю розміру ((M + 1) × (M + 1))
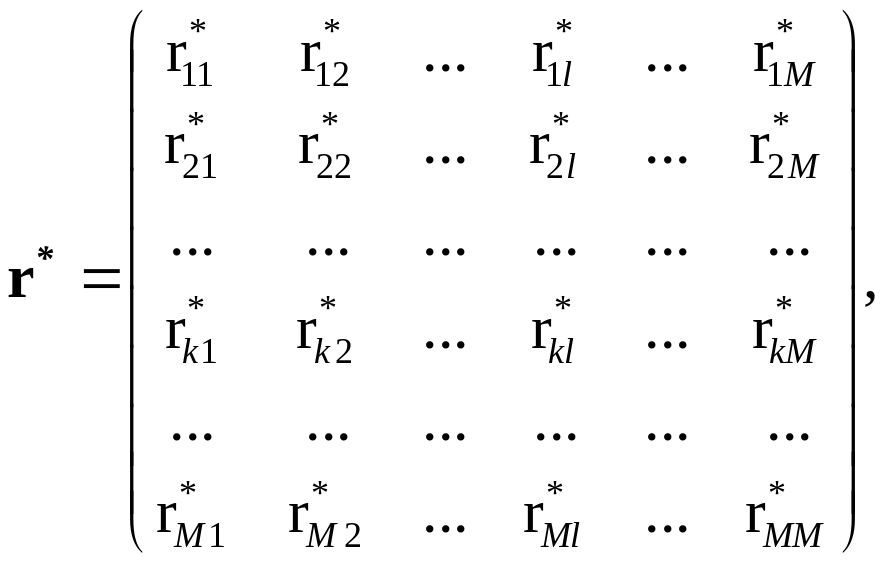(9.65)
кожен елемент якої –
(9.66)
де Aij – алгебраїчні доповнення до елемента rij матриці r коефіцієнтів парної кореляції, а Сij – елементи матриці, оберненої до останньої.
32. Властивості оцінок параметрів регресійної моделі. Значення aj j-ої оцінки параметра αj (j = 1, …, M) регресійної моделі, як правило, є результатом оцінювання по даних випадкової вибірки {Y; Xj} об’єму n – реалізацій n значень {yi} результативної ознаки Y і n значень {xji} кожної j-ої факторної ознаки Xj (i = 1, …, n). Тобто значення aj можна розглядати як числове значення випадкової величини Aj, що вимагає надійності вибіркової оцінки Aj. Надійною вважається така вибіркова оцінка, яка є слушною, незміщеною, ефективною й інваріантною.
Ці властивості мають відношення і до інших оцінок параметрів ГСС, з якої утворюється вибірка спостережень об’єму n, а саме, до вибіркових дисперсій, коваріаційних моментів, коефіцієнтів детермінації та кореляції, істинні (справжні) невідомі значення яких, за умов значущості їх оцінок, визначаються наближено, інтервально, на рівні значущості α певного критерію.
33. Слушна оцінка – вибіркова оцінка Aj параметра αj регресійної моделі є слушною, якщо для будь-якого завгодно малого додатного числа δ вона задовольняє рівності
(9.67)
Для слушних оцінок, здобутих на основі МНК за умови детермінованості факторного зв’язку, має виконуватись рівність
(9.68)
де Q – додатно визначена матриця.
34. Незміщена оцінка – вибіркова оцінка Âj параметра αj регресійної моделі є незміщеною, якщо її математичне сподівання М(Âj) дорівнює значенню параметра:
(9.69)
Зміщеною
є така оцінка, яка дає зміщення θ
в оцінці
параметра –
Зміщеність оцінки має місце внаслідок нерепрезентативності вибірки або за наявності похибок специфікації, що потребує відповідного оцінювання. Враховуючи те, що справжні значення параметрів невідомі, оцінювання величини зміщення кожної оцінки здійснюється за результатами аналізу відповідних відношень:
(9.70)
де
і
–
відповідно модуль числового значення
aj
оцінки Aj
і незміщена середня квадратична похибка
(СКП) оцінювання параметра αj,
або стандартна
похибка коефіцієнта регресії,
така, що
(9.71)
де bjj – елементи головної діагоналі матриці (Х'Х)-1;
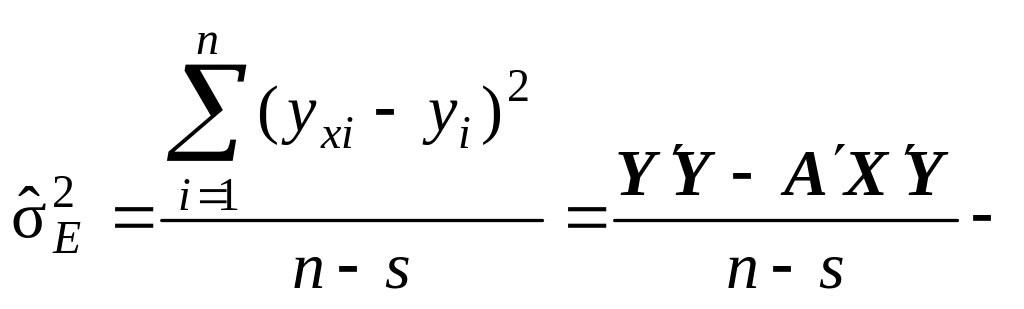(9.72)
незміщена
оцінка вибіркової залишкової дисперсії
–
стандартна
похибка регресії,
визначена для M-факторної
моделі з s
оцінюваними параметрами (s
= M
+ 1).
разом
з оцінками коваріації між Aі
і Aj
(i ≠
j)
утворюють коваріаційну матрицю
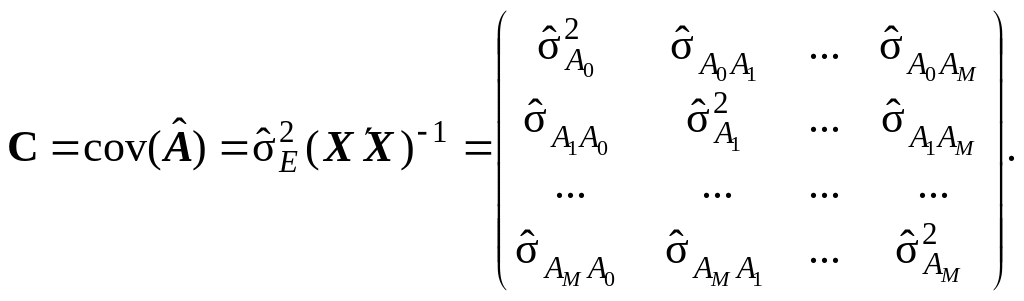(9.73)
Коваріаційний момент, який характеризує коваріацію між двома будь-якими вибірковими оцінками Аk і Аl коефіцієнтів регресії αk і αl, може бути представлений формулою:
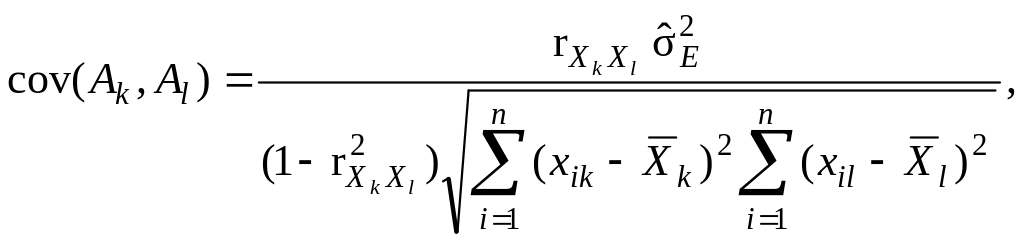(9.74)
де – парний коефіцієнт кореляції змінних Xk і Xl.
Якщо
,
то зміщенням можна нехтувати, як
незначним, а оцінку параметра можна
вважати незміщеною; якщо
,
то зміщення є значним, і оцінка параметра
є зміщеною; k – припустимий відсоток зміщення, який, зазвичай, встановлюють на рівні 5%.
Перевірка
якості регресії із застосуванням
елементів дисперсійного аналізу вимагає
у формулах для обчислення вибіркових
індексів детермінації та коефіцієнтів
кореляції забезпечити незміщеність
вибіркових дисперсій
,
.
35.
Ефективна
оцінка –
вибіркова оцінка Aj
параметра αj
регресійної моделі є ефективною, якщо
вона задовольняє умовам теореми
Гауса-Маркова, тобто коли дисперсія
цієї
оцінки, визначеної методом найменших
квадратів, є найменшою серед дисперсій
усіх
інших незміщених оцінок цього Aj
параметра,
визначених іншими методами:
Інакше,
деяка оцінка (обов’язково незміщена
та слушна) Aj
параметра αj
регресійної моделі є ефективною, якщо
існує дисперсія D(Âj),
яка дорівнює нижній грані
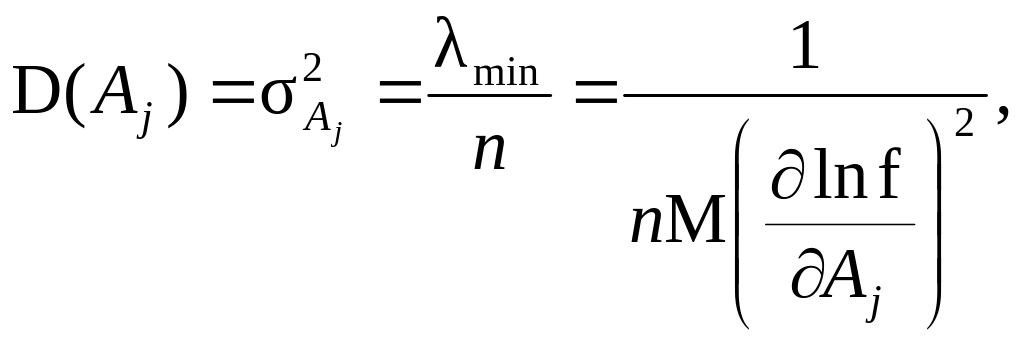де
f
– щільність розподілу ймовірностей
випадкової величини Aj.
Асимптотична ефективність е∞{Aj} = λmin/λ такої оцінки вимірює розсіювання асимптотичного розподілу навколо параметра αj.
Незміщені
вибіркові дисперсії
і
,
обчислені по результатах вибірки об’єму
n,
які застосовуються в дисперсійному
аналізі для оцінки детермінованості
факторного зв’язку з s
оцінюваними параметрами
αj,
мають ефективність (n
– 1)/n
і (n –
s)/n
відповідно, тобто
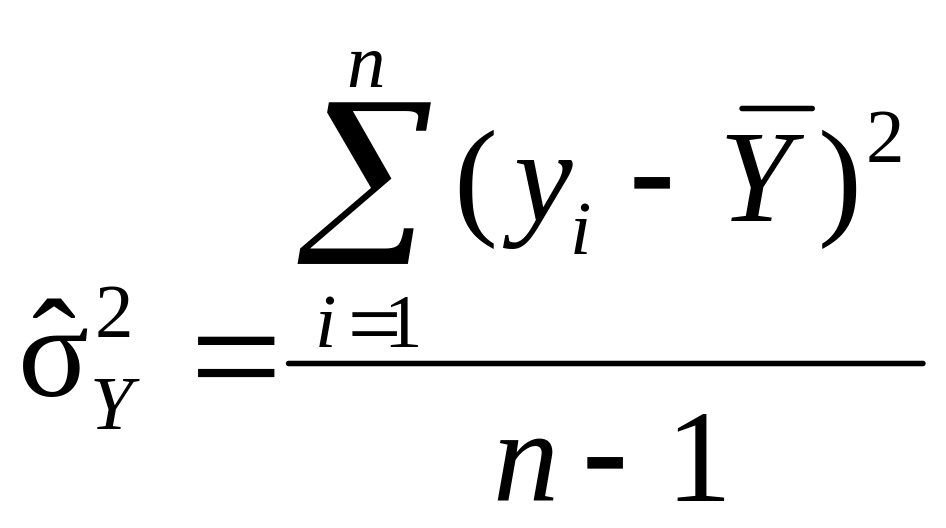і
(9.75)
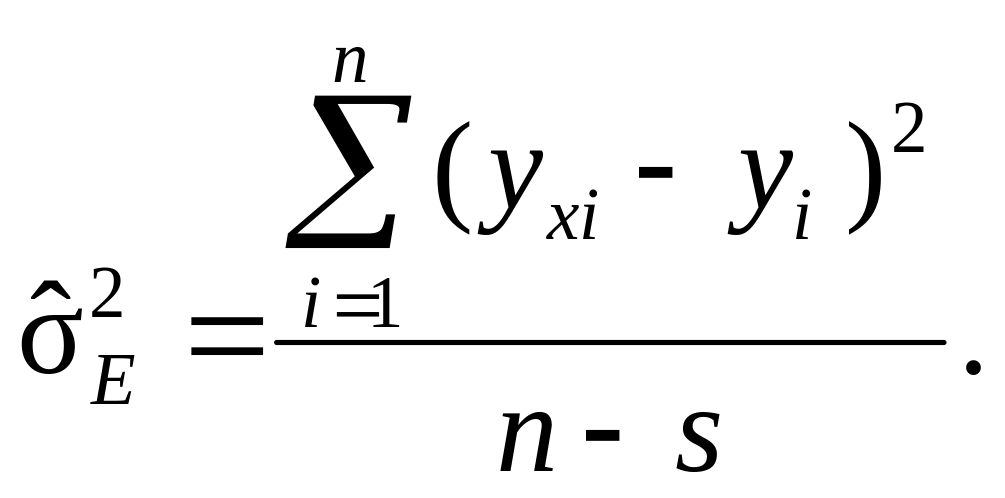(9.76)
36. Інваріантна оцінка – вибіркова оцінка Aj параметра αj регресійної моделі є інваріантною, якщо для функції g, яка характеризує факторний зв’язок залежної змінної Y та відповідної пояснювальної змінної Xj (її лінійний приклад), заміна αj на числове значення aj оцінки Aj не змінює вид функціональної залежності змінних Y і Xj.
37. Значущість оцінки – перевірка нульової статистичної гіпотези H0 щодо характеристики факторного зв’язку, даної по відповідній оцінці параметра цього зв’язку, здійснюється за певними критеріями значущості шляхом визначення, чи є оцінка значущою і гіпотеза спростовується (відкидається як хибна), чи оцінка не є значущою і гіпотеза підтверджується (вважається істиною), інакше, критерій «контролює» статистичну гіпотезу H0. Значущою є така вибіркова оцінка Ý параметра η факторного зв’язку, відносно якої фактичне значення λÝ певного критерію значущості (для деяких критеріїв – |λÝ|) перевищує критичне його значення λкр. на заданому рівні значущості α критерію –
(9.77)
Фактичне значення критерію обчислюється по результатах вибірки {Y; Xj} об’єму n – реалізацій n значень {yi} результативної ознаки Y і n значень {xji} кожної j-ої факторної ознаки Xj (j = 1, …, M; i = 1, …, n).
Перевірку на значущість проходять оцінки коефіцієнтів регресії αj, індексів детермінації R² та коефіцієнтів кореляції r. Така перевірка стає можливою при виконанні передумов МНК.
38.
Інтервальна
оцінка параметра.
За умов «нормальності» реалізацій
вибіркових спостережень оцінка параметра
η
факторного зв’язку виконується в межах
(границях) довірчого інтервалу, які
визначаються симетрично відносно
вибіркової оцінки Ý
= ẏ
цього параметра на відстані граничної
похибки оцінювання
:
(9.78)
де
λкр.(α)
– теоретичне критичне (табличне) значення
певного критерію на рівні значущості
α,
інакше – коефіцієнт довіри;
–
середня квадратична похибка оцінювання
параметра η.
Довірчий інтервал «накриває» параметр зв’язку із заданим рівнем значущості α; його довжина і положення на осі значень оцінюваного параметра є випадковими.
39. Значущість оцінки коефіцієнта (оцінок коефіцієнтів) лінійної регресії. Перевірка значущості вибіркової оцінки Aj = aj коефіцієнта αj лінійної регресії Y на Xj здійснюється за t-критерієм: оцінка є значущою, якщо модуль фактичного значення
(9.79)
(відношення
Стьюдента)
двостороннього t-критерію
перевищує його критичне значення tкр.
на заданому
рівні значущості
α –
–
середня квадратична похибка оцінювання
параметра αj,
tкр.
– це верхня
границя критичної області, яка є квантилем
t-розподілу
tm;1-α/2
= |t|m;1-α
порядку
1 – α/2
(1 – α) з
кількістю ступенів свободи m
= n
– s
(n
– об’єм
вибірки, s
– кількість оцінюваних параметрів
моделі).
Фактичне
значення
t-критерію
обчислюється по результатах вибірки
об’єму n у
припущенні, що
αj
= 0 (нульова
гіпотеза Н0:
Y
не залежить від Xj),
тобто
Отже,
за умови
коли
фактичне значення критерію потрапляє
в критичну область, t-критерій,
контролюючи гіпотезу про відсутність
залежності Y
від Xj,
дає підстави вважати гіпотезу хибною,
а змінну Y –
залежною від змінної Xj.
Надійність
критерію ґарантується, якщо результативна
ознака Y
при кожному фіксованому значенні xji
j-ої
факторної ознаки Xj
(j
= 1, …, M;
i = 1, …, n)
має бути нормально розподіленою
випадковою величиною з математичним
сподіванням
і
дисперсією, не залежною від зміни Xj
(передумова
застосування критерію).
У протилежному випадку значущість
оцінок коефіцієнтів регресії не гарантує
високої якості рівняння регресії.
Для вибіркових оцінок коефіцієнтів регресії α0 і α1 однофакторної регресійної моделі відповідні фактичні значення t-критерію можна визначити в такий спосіб:
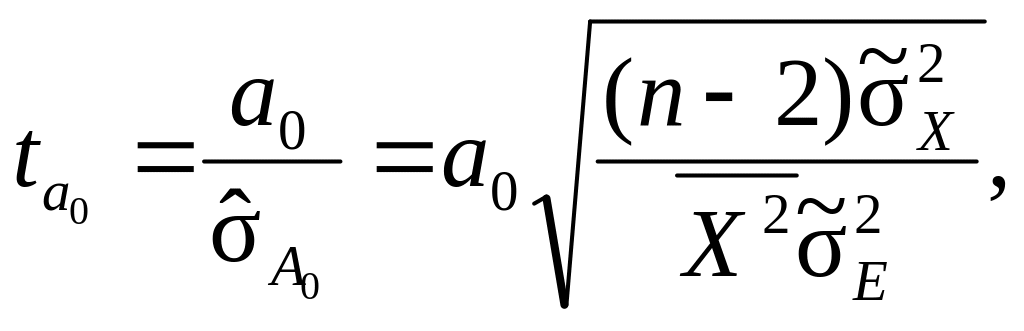
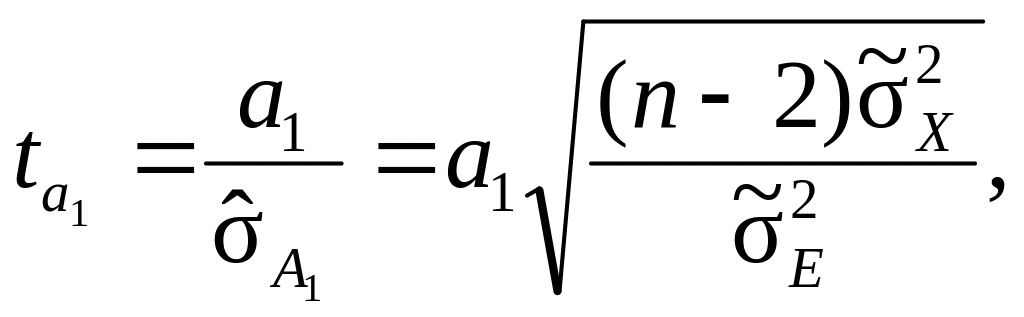(9.80)
де
і
–
відповідно зміщені вибіркові оцінки
залишкової дисперсії і дисперсії
факторної ознаки Х.
Якщо вибіркова оцінка коефіцієнта регресії αj виявляється незначущою, фактор при ньому виключається з регресійної моделі й оцінювання параметрів повторюється, але з іншим фактором на місці колишнього.
Іноді точна перевірка замінюється звичайним порівняльним аналізом (грубою оцінкою):
-
якщо |t|
< 1 (|aj|
<
),
то оцінка є статистично незначущою;
- якщо 1 < |t| < 2 (|aj| < 2 ), то оцінка є відносно значущою і потребує табличного уточнення;
- якщо 2 < |t| < 3, то оцінка є значущою, що гарантовано для n > 30 і α > 0,05;
- якщо |t| > 3, то оцінка є сильно значущою й імовірність похибки не перевищує 0,001.
Для значущої оцінки визначаються границі довірчого інтервалу відповідного коефіцієнта регресії αj.
Оцінюючи значущість оцінок коефіцієнтів регресії усіх разом, можна перевірити загальну якість регресійної моделі. Сукупна їх значущість перевіряється за F-критерієм: оцінка є значущою, якщо модуль його фактичного значення
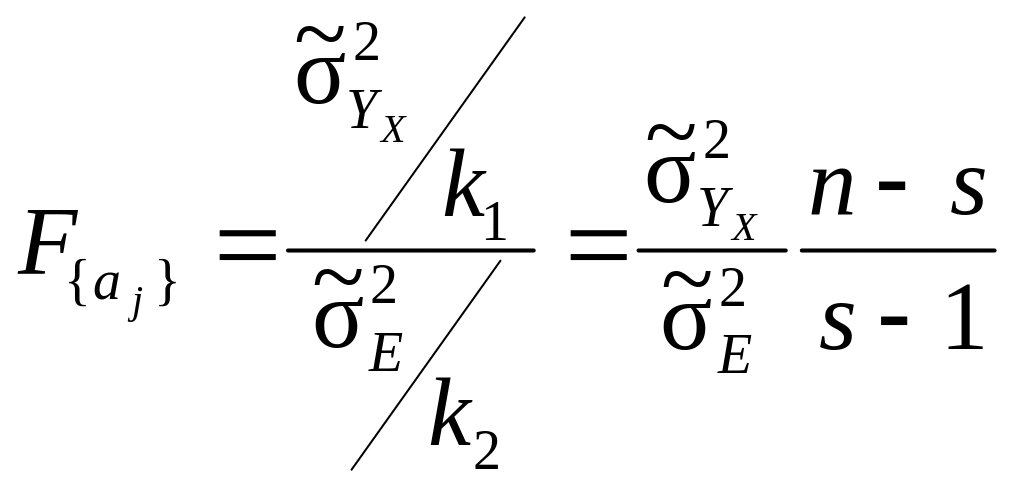(9.81)
перевищує
критичне його значення Fкр.
на заданому
рівні значущості
α –
і
–
вибіркові відповідно факторна і залишкова
дисперсії. Fкр.
– це верхня
границя критичної області, яка є квантилем
F-розподілу,
,
порядку 1 – α
з кількістю ступенів свободи k1
= s
– 1 і k2
= n
– s
(n –
об’єм вибірки, s
– кількість оцінюваних параметрів
моделі).
Фактичне
значення
F-критерію
обчислюється по результатах вибірки
об’єму n у
припущенні, що
α0
= α1
= … = αM
= 0 (нульова
гіпотеза Н0:
Y
не залежить від {Xj}),
тобто
=
.
Отже,
за умови
коли
фактичне значення критерію потрапляє
в критичну область, F-критерій,
контролюючи гіпотезу про відсутність
залежності Y
від {Xj},
дає підстави вважати гіпотезу хибною,
факторну дисперсію значно більшою, ніж
залишкова дисперсія, а змінну Y
– суттєво
залежною від кожної пояснювальної
змінної Xj.
Причому,
і
мають
розглядатись як незалежні випадкові
величини, що мають χ²-розподіл
відповідно з k1
= s
– 1 і k2
= n
– s
ступенями
свободи (передумова
застосування критерію).
На відміну від такої перевірки загальної якості регресійної моделі, частіше застосовується перевірка значущості множинного коефіцієнта детермінації.
40.
Довірчий
інтервал
(Iα)
коефіцієнта
регресії –
границі довірчого інтервалу коефіцієнта
регресії αj
для значущої вибіркової оцінки Аj,
яка є випадковою величиною з симетричним
розподілом, визначаються симетрично
відносно її значення аj
на відстані граничної похибки оцінювання
:
(9.82)
де |t|m;1-α – теоретичне (табличне, Д.4) значення двостороннього t-критерію на рівні значущості α з кількістю ступенів свободи m = n – s (n – об’єм вибірки, s – кількість оцінюваних параметрів моделі); – незміщена середня квадратична похибка оцінювання параметра αj.
41.
Значущість
оцінки коефіцієнта
(індексу)
детермінації.
Перевірка значущості вибіркової оцінки
коефіцієнта детермінації R² одно- чи
багатофакторного зв’язку здійснюється
за F-критерієм:
оцінка є значущою, якщо фактичне значення
(9.83)
F-критерію
перевищує його критичне значення Fкр.
на рівні значущості α
–
Fкр.
– це верхня
границя критичної області, яка є квантилем
F-розподілу,
,
порядку 1 – α
з кількістю ступенів свободи k1
= s
– 1 і k2
= n
– s
(n –
об’єм вибірки, s
– кількість оцінюваних параметрів
моделі).
Фактичне значення F-критерію обчислюється по результатах вибірки об’єму n у припущенні, що R² = 0 (нульова гіпотеза Н0: Y не залежить від X({Xj})).
Отже,
за умови
коли
фактичне значення критерію потрапляє
в критичну область, F-критерій,
контролюючи гіпотезу про відсутність
залежності Y
від X({Xj}),
дає підстави вважати гіпотезу хибною,
а змінну Y –
суттєво залежною від X-фактора(-ів).
Надійність критерію ґарантується, якщо виконуються передумови МНК. У протилежному випадку, навіть при наближеності R² до одиниці, значущість останнього не ґарантує високої якості рівняння регресії.
Для
вибіркової оцінки парного коефіцієнта
детермінації
однофакторної
регресійної моделі фактичне значення
F-критерію
можна визначити в такий спосіб:
(9.84)
Для лінійної регресії, яка представляє однофакторний зв’язок, перевірка значущості коефіцієнта детермінації дає аналогічний результат, що й перевірка значущості відповідного коефіцієнта кореляції, коли фактичне значення F-критерію для коефіцієнта детермінації є квадратом значення t-критерію для відповідного коефіцієнта кореляції, що вказує на тотожність цих перевірок. Самостійної важливості коефіцієнт детермінації набуває у випадках множинної лінійної регресії.
42.
Значущість
оцінки коефіцієнта кореляції.
Перевірка значущості вибіркової оцінки
коефіцієнта
кореляції r одно- чи багатофакторного
зв’язку здійснюється за t-критерєм:
оцінка є значущою, якщо фактичне значення
(9.85)
двостороннього
t-критерію
перевищує його критичне значення
на
рівні значущості α
–
tкр.
– це верхня
границя критичної області, яка є квантилем
t-розподілу,
,
порядку 1 – α
з кількістю ступенів свободи m
= n
– s
(n –
об’єм вибірки, s
– кількість оцінюваних параметрів
моделі).
Фактичне
значення
t-критерію
обчислюється по результатах вибірки
об’єму n у
припущенні, що
=
0 (нульова гіпотеза Н0:
Y
лінійно не залежить від X({Xj},
j
= 1, 2, …, M)).
Отже,
за умови
коли
фактичне значення критерію потрапляє
в критичну область, t-критерій,
контролюючи гіпотезу про відсутність
лінійної залежності Y
від X({Xj}),
дає підстави вважати гіпотезу хибною,
а змінну Y –
лінійно залежною від X-фактора(-ів).
Аналогічно побудований критерій для перевірки значущості частинних коефіцієнтів кореляції між двома ознаками при елімінації лінійного впливу решти (M – 1) ознак за умови, що їх спільний (M + 1)-мірний розподіл є нормальним.
Для лінійної регресії, яка представляє однофакторний зв’язок, фактичне значення t-критерію є квадратним коренем із значення F-критерію для відповідного коефіцієнта детермінації:
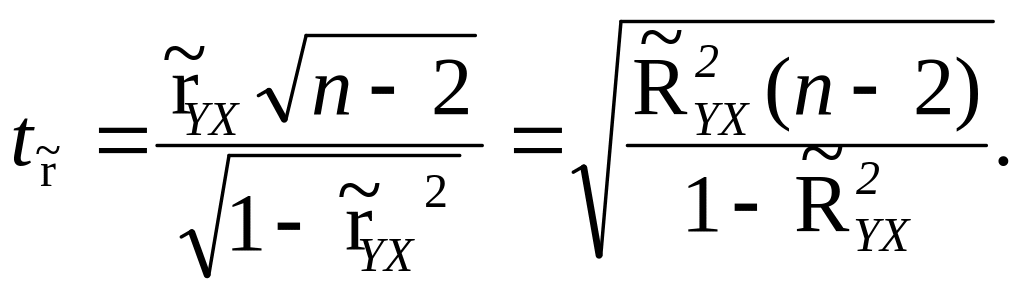(9.86)
У цьому випадку нульову гіпотезу Н0 можна, до того ж, перевірити, порівнюючи значення вибіркового коефіцієнта кореляції з його критичним значенням –
(9.87)
Якщо
,
то гіпотеза
Н0
спростовується. Для критичних значень
коефіцієнта кореляції побудовані
статистичні таблиці.
43.
Довірчий
інтервал
(Iα)
коефіцієнта
кореляції.
Границі довірчого інтервалу коефіцієнта
кореляції r для значущої вибіркової
його оцінки, яка є випадковою величиною
із симетричним розподілом, визначаються
симетрично відносно її значення
на відстані граничної похибки оцінювання
:
(9.88)
де – теоретичне (табличне, Д.4) значення двостороннього t-критерію на рівні значущості α з кількістю ступенів свободи m = n – s (n – об’єм вибірки, s – кількість оцінюваних параметрів моделі);
–
(9.88`)
незміщена середня квадратична похибка оцінювання параметра r.
Поширеною є задача визначення границь (двостороннього) довірчого інтервалу для парного коефіцієнта кореляції rYX двомірної нормальної генеральної сукупності (залежна змінна Y і один X-фактор) із заданою довірчою ймовірністю по результатах вибірки
об’єму
n. Однак,
навіть для вибірок об’єму n
> 30, розподіл
вибіркового коефіцієнта кореляціє
може
відрізнятись від нормального, і він
стає несиметричним. Це може призвести
до некоректності у визначенні границь
відповідного довірчого інтервалу, коли
|rYX|
> 1. За таких умов корисним є уведення
нової випадкової величини Z
(перетворення
Фішера), яка
набуває значень
(9.89)
і при n > 10 розподілена наближено нормально з центром і дисперсією
Зворотне перетворення дає:
(9.90)
Тоді, за умови значущості оцінки , коректними є границі довірчого інтервалу, визначені в такий спосіб:
(9.91)
де
–
коефіцієнт довіри – квантиль u-розподілу
на рівні значущості α.
Аналогічно визначаються коректні границі довірчих інтервалів для частинних коефіцієнтів кореляції.
44.
Довірчий
інтервал
(Іα)
прогнозу
середнього значення результативної
ознаки – це
інтервал можливих значень середнього
значення
результативної
ознаки Y,
який має місце при певних (заданих,
очікуваних) значеннях хpj
факторних ознак Xj
(j
= 1, 2, …, M)
із заданою імовірністю Р
= 1 – α,
де α
– рівень значущості t-критерію,
покладеного в основу визначення похибки
інтервального оцінювання.
Якщо
справжнє значення
розглядати
як умовне математичне сподівання
М(Y|{Xj
= xpj}),
значення
регресії
–
як нормально розподілену випадкову
величину
з параметрами
і
(αj
– коефіцієнти регресії Y
на {Xj},
оцінки яких аj
теж нормально розподілені), а також
припустити, що різниця між
і
значенням
не перевищує граничну похибку інтервальної
оцінки із заданою ймовірністю Р
= 1 – α,
то границі довірчого інтервалу прогнозу
можна визначити в такий спосіб:
(9.92)
де
–
теоретичне (табличне, Д.4) значення
двостороннього t-критерію
на рівні значущості α
з кількістю ступенів свободи m
= n
– s
(n –
об’єм вибірки, s
– кількість оцінюваних параметрів
моделі);
– середньоквадратична
похибка
визначення
(прогнозу), пропорційна незміщеній
оцінці
залишкового СКВ; Хр
– вектор-стовпець заданих значень хpj
факторних ознак Xj.
Для однофакторної моделі (парної регресії) цей інтервал визначається в такий спосіб:
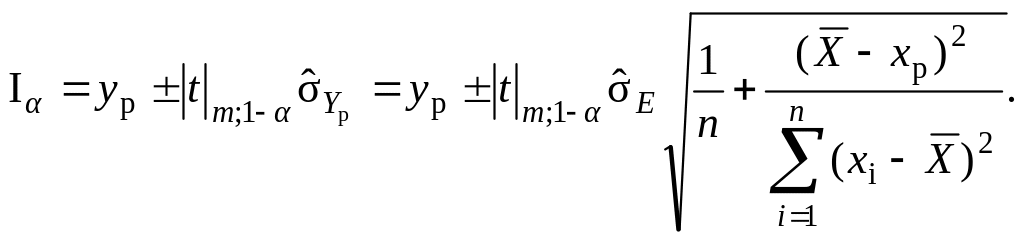(9.93)
45. Довірчий інтервал (Іα) прогнозу індивідуального значення результативної ознаки – це інтервал можливих значень індивідуального значення у0 результативної ознаки Y, який має місце при певних (заданих, очікуваних) значеннях хpj факторних ознак Xj (j = 1, 2, …, M) із заданою імовірністю Р = 1 – α, де α – рівень значущості t-критерію, покладеного в основу визначення похибки інтервального оцінювання.
Якщо
справжнє значення у0
розглядати
як значення нормально розподіленої
випадкової величини Y0
–
,
а значення ур
регресії
як
значення нормально розподіленої
випадкової величини Yр
–
,
а також припустити, що Y0
і Yр
незалежні,
й отже, випадкова величина U
= Y0
– Yр
теж нормальна –
,
і що різниця між у0
і ур
не перевищує граничну похибку інтервальної
оцінки із заданою ймовірністю Р
= 1 – α,
то границі довірчого інтервалу прогнозу
можна визначити в такий спосіб:
(9.94)
де
–
теоретичне (табличне) значення
двостороннього t-критерію
на рівні значущості α
з кількістю ступенів свободи m
= n
– s
(n –
об’єм вибірки, s
– кількість оцінюваних параметрів
моделі);
–
середньоквадратична похибка визначення
у0
(прогнозу), пропорційна незміщеній
оцінці
залишкового СКВ; Хр
– вектор-стовпець заданих значень хpj
факторних ознак Xj.
Для однофакторної моделі (парної регресії) цей інтервал визначається в такий спосіб:
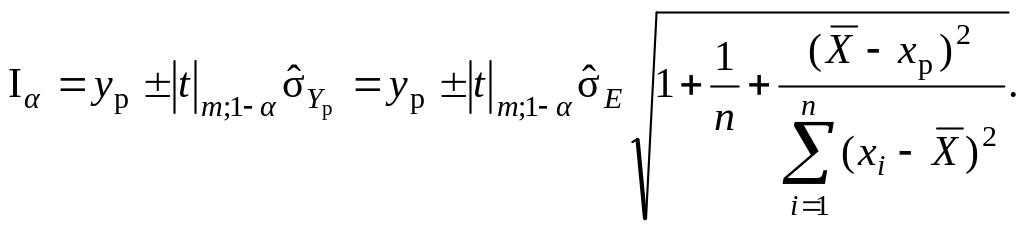(9.95)
46. Оцінка прогнозних можливостей регресійної моделі. Модель регресії може бути визнана якісною, якщо отримані на її основі прогнози підтверджуються реальністю.
Критеріями прогнозних якостей можуть бути обрані деякі з наступних співвідношень.
1) Коефіцієнт варіації –
(9.96)
де
–
незміщена оцінка залишкового СКВ;
–
середнє арифметичне значення залежної
змінної.
Якщо υ < 5 % і відсутня автокореляція залишків (визначається з величини статистики Дарбіна-Уотсона), то прогнозні якості моделі високі.
2) Середня відносна похибка прогнозу (М.А.Р.Е.) –
(9.97)
певну величину якої співвідносять з якісною оцінкою прогнозних можливостей за такою шкалою:
-
№
п/п
Рівень
М.А.Р.Е. (%)
Якість прогнозних
можливостей
1.
<10
Висока
2.
10-20
Достатня
3.
20-50
Задовільна
4.
>50
Незадовільна
3) Коефіцієнт відповідності Тейла –
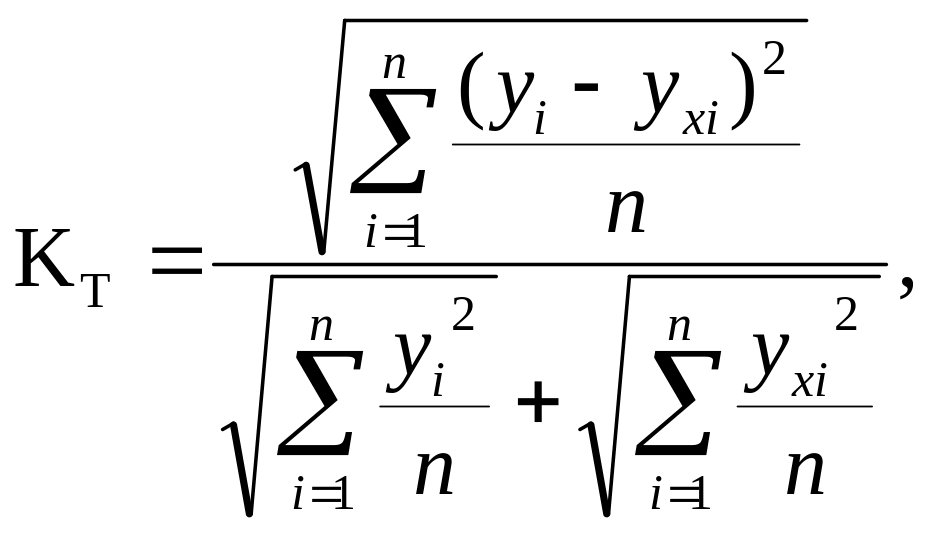(9.98)
який має бути якомога ближчим до нуля, щоб модель мала високі прогнозні можливості.
Прогнозні якості перевіряються в період часу, наступний за періодом, в якому оцінювалось рівняння регресії, і цей період має бути, принаймні, втричі коротший за останній.
47. Перевірка виконуваності передумов застосування МНК. Виконуваність передумов застосування МНК в КРАЗ перевіряється на предмет виявлення та можливого попередження похибок специфікації регресійної моделі, пов’язаних з автокореляцією залишків, гетероскедастичністю, мультиколінеарністю17.
48. Тристадійний відбір факторів – це відбір факторів для побудови багатофакторних регресійних моделей з використанням статистичних і математичних критеріїв; виконується в три стадії.
Перша стадія. Застосовується апріорний аналіз і на фактори попередньої моделі не накладається особливих обмежень.
Друга стадія. Здійснюється порівняльна оцінка і відсів частини факторів шляхом співставлення парних коефіцієнтів кореляції, вимірюючи тісноту зв’язку кожної пояснювальної змінної із залежною змінною та пояснювальних змінних між собою за таким критерієм:
(9.99)
Для цього зручно застосовувати кореляційну матрицю.
Третя стадія. Здійснюється завершальний відбір факторів шляхом аналізу значущості вектора оцінок параметрів різних варіантів рівняння множинної регресії з використанням t-критерію.
49. Перевірка рівності двох коефіцієнтів детермінації. Виконується для двох рівнянь регресії, які пов’язують результативну змінну Y з М і (М ± К) пояснювальними змінними та характеризуються коефіцієнтами детермінації R1² і R2² відповідно, причому форма цієї залежності від одних і тих самих змінних в обох рівняннях однакова, а також незмінним є об’єм вибірки. Знак «мінус» показує, що з моделі виключається К змінних, а знак «плюс» – додатково добавляються в модель К змінних.
Якщо припустити, що якість рівняння не змінюється, тобто погіршення (покращання) якості R1² – R2² = 0 (R2² – R1² = 0), або дорівнюють нулю коефіцієнти регресії при виключених (добавлених) факторах (нульова гіпотеза Н0), то перевірка гіпотези здійснюється за F-критерієм, значення якого обчислюються в такий спосіб:
(9.100)
якщо з другого рівняння виключаються К пояснювальних змінних (М – К) і сподіваною є нерівність R1² ≥ R2²;
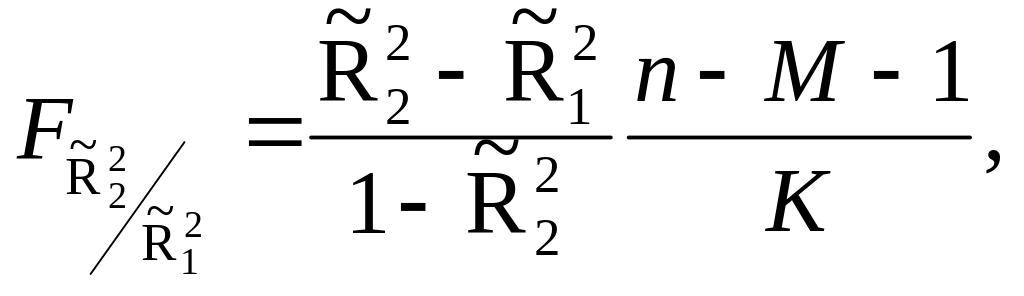(9.101)
якщо в друге рівняння додатково добавити К пояснювальних змінних (М + К) і сподіваною є нерівність R2² ≥ R1².
Якщо гіпотеза Н0 є справедливою, F-статистика має розподіл Фішера з k1 = K і k2 = n – M – 1 ступенями свободи.
За
умови
де
–
критичне значення F-критерію,
гіпотеза Н0
спростовується на рівні значущості α
F-критерію,
в першому випадку є некоректним виключення
з моделі відразу К
факторів, а в другому випадку добавлення
в модель К
додаткових факторів є виправданим і
пояснює значну частину непоясненої
раніше дисперсії залежної змінної Y.
На практиці уведення в модель пояснювальних змінних, як правило, виконується по одній.
50. Перевірка гіпотези про збіжність рівнянь регресії для двох вибірок (тест Чоу). Виконується для двох вибірок об’єму n1 і n2 з однією формою рівняння регресії в припущенні, що параметри першого і другого рівнянь однакові – Н0: αj1 = αj2 (j = 0, 1, …, M).
Нехай
і
–
залишкові дисперсії першого і другого
рівнянь регресії відповідно й по
об’єднаній вибірці об’єму (n1
+ n2)
оцінено ще одне рівняння регресії із
залишковою дисперсією
,
тоді гіпотеза Н0
перевіряється за допомогою F-статистики
(9.102)
Якщо гіпотеза Н0 є справедливою, F-статистика має розподіл Фішера з k1 = M + 1 і k2 = n1 + n2 – 2M – 2 ступенями свободи.
За
умови
де
–
критичне значення F-критерію,
фактичне значення F-критерію
наближається до нуля,
,
що відповідає практичній збіжності
двох рівнянь регресії. У протилежному
випадку гіпотеза Н0
спростовується на рівні значущості α
F-критерію.
Тест дозволяє визначитись з побудовою єдиного рівняння регресії або з потребою розбити весь час на частини з побудовою в межах кожної з них свого рівняння регресії?
Контрольні питання:
1. Кореляційно-регресійний аналіз зв’язків: сутність і завдання методу; поняття факторної та результативної ознак; мета кореляційного та регресійного аналізу; види зв’язків.
2. Одно- і багатофакторний зв’язок, кореляційний і функціональний зв’язок: зміст, форми подання.
3. Регресія: визначення, види, форми подання парної та множинної регресії.
4. Регресійна модель: зміст, загальний вид рівняння регресії, специфікація моделі, похибки специфікації.
5. Аналітичне вирівнювання кореляційного зв’язку: зміст, МНК щодо оцінки параметрів моделі регресії, передумови застосування МНК.
6. Адекватне рівняння регресії, критерії визначення адекватного рівняння.
7. Парна регресія (кореляція): поняття; види рівнянь регресії результативної ознаки на факторну; метод найменших квадратів (МНК) щодо розрахунку оцінок параметрів лінійної моделі регресії.
8. Детермінованість і стохастичність факторного зв’язку, методи оцінки.
9. Властивості оцінок регресії та перевірка їх значущості; інтервальне оцінювання.
10. Лінійний коефіцієнт регресії: зміст, порядок визначення, оцінка коефіцієнта та перевірка значущості оцінки; визначення границь довірчого інтервалу.
11. Індекс (коефіцієнт) детермінації: зміст і порядок визначення; факторна, залишкова і загальна дисперсії та їх зв’язок.
12. Множинний і парний коефіцієнт детермінації: зміст, порядок визначення, оцінка коефіцієнта та перевірка значущості оцінки.
13. Частинний коефіцієнт детермінації: зміст, порядок визначення.
14. Перевірка рівності двох коефіцієнтів детермінації щодо загальної оцінки якості рівняння регресії.
15. Перевірка гіпотези про збіжність рівнянь регресії для двох вибірок (тест Чоу) щодо загальної оцінки якості рівняння регресії.
16. Коваріація: зміст, коваріаційний момент і коваріаційна матриця; коефіцієнт кореляції.
17. Множинний і парний коефіцієнт кореляції: зміст, порядок визначення, оцінка коефіцієнта та перевірка значущості оцінки; визначення границь довірчого інтервалу.
18. Частинний коефіцієнт кореляції: зміст, порядок визначення, матриця частинних коефіцієнтів.
19. Перевірка виконуваності передумов застосування МНК.
20. Автокореляція залишків: зміст, способи визначення і методи запобігання; критерій Дарбіна-Уотсона.
21. Гетероскедастичність: зміст, способи визначення і методи запобігання.
22. Мультиколінеарність: зміст, способи визначення і методи запобігання; тристадійний відбір факторів.
23. Довірчий інтервал прогнозу середнього значення результативної ознаки.
24. Довірчий інтервал прогнозу індивідуального значення результативної ознаки.
25. Оцінка прогнозних можливостей моделі.