
- •Передмова
- •Глава 1.
- •1.1. Основні теоретичні положення
- •3. Розрізняють такі статистичні ознаки:
- •5. Розрізняють такі статистичні показники:
- •1.2. Тестові завдання
- •Глава 2.
- •2.1. Основні теоретичні положення
- •25. Види сс:
- •34. Форми організації сс:
- •43. Розрізняють похибки:
- •2.2. Задачі
- •2.2.1. Типова задача
- •2.2.2. Варіанти початкових даних
- •2.3. Тестові завдання
- •Глава 3.
- •3.1. Основні теоретичні положення
- •3.2. Задачі
- •3.2.1. Типові задачі
- •3.2.2. Варіанти початкових даних
- •3.3. Тестові завдання
- •Глава 4.
- •4.1. Основні теоретичні положення
- •4.2. Задачі
- •4.2.1. Типові задачі
- •4.2.2. Варіанти початкових даних
- •4.3. Тестові завдання
- •Глава 5.
- •5.1. Основні теоретичні положення
- •5.2. Задачі
- •5.2.1. Типові задачі
- •За планом
- •5.2.2. Варіанти початкових даних
- •5.3. Тестові завдання
- •Глава 6.
- •6.1. Основні теоретичні положення
- •6.2. Задачі
- •6.2.1. Типові задачі
- •Розрахункова таблиця
- •6.2.2. Варіанти початкових даних
- •6.3. Тестові завдання
- •16. Яка вибіркова оцінка є незміщеною? _______________________________.
- •Глава 7.
- •7.1. Основні теоретичні положення
- •7.2. Задачі
- •7.2.1. Типові задачі
- •Розрахункова таблиця
- •Розрахункова таблиця
- •88,81 Тис.Грош.Од.
- •7.2.2. Варіанти початкових даних
- •7.3. Тестові завдання
- •Глава 8.
- •8.1. Основні теоретичні положення
- •8.2. Задачі
- •8.2.1. Типові задачі
- •8.2.2. Варіанти початкових даних
- •Глава 9.
- •9.1. Основні теоретичні положення
- •9.2. Задачі
- •9.2.1. Типові задачі
- •9.2.2. Варіанти початкових даних
- •Для нотаток
- •Значення функції
- •Додаток 2 Інтеграл ймовірностей
- •Додаток 5 Критичні значення f-критерію
- •Додаток 6 Критичні значення Kn;α для статистики критерію Колмлогорова
- •Література
- •Грецький алфавит
- •Латинський алфавит
Середній рівень
=
88,81 Тис.Грош.Од.


12
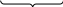
2-й рік
3-й рік
1-й рік
Рис. 1. Динаміка місячних змін середньоденного товарообороту протягом 1-3-го років:
ряд 1 – фактична; ряд 2 – теоретична, отримана методом рядів Фур’є
(по першій гармоніці); ряд 3 – теоретична, отримана методом рядів Фур’є
(по першій-третій гармоніках)
2) Методом постійного середнього побудуємо сезонну хвилю середньоденного товарообороту протягом умовного року, для чого визначимо місячні значення середнього індексу сезонності. Середній індекс сезонності умовного місяця обчислюється по відповідних місячних значеннях індексів сезонності усіх трьох років. Індекси сезонності визначаються як співвідношення відповідних фактичних значень рівня ряду динаміки (з таблиці) і середнього значення рівня. Для зручності результати проміжних розрахунків зведемо в розрахункову таблицю.
Розрахункова таблиця
i |
yij |
|
|
|
||
j = 1 |
j = 2 |
j = 3 |
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
83,40 |
87,80 |
80,10 |
251,30 |
83,766667 |
94,325931 |
2 |
84,30 |
88,40 |
81,50 |
254,20 |
84,733333 |
95,414451 |
3 |
85,90 |
88,50 |
89,40 |
263,80 |
87,933333 |
99,017829 |
4 |
86,10 |
90,40 |
88,60 |
265,10 |
88,366667 |
99,505787 |
5 |
79,30 |
78,20 |
82,20 |
239,70 |
79,900000 |
89,971849 |
6 |
107,90 |
113,40 |
115,00 |
336,30 |
112,100000 |
126,23084 |
7 |
106,00 |
97,40 |
105,80 |
309,20 |
103,066667 |
116,05880 |
8 |
86,30 |
80,00 |
87,60 |
253,90 |
84,633333 |
95,301845 |
9 |
90,70 |
90,90 |
83,90 |
265,50 |
88,500000 |
99,655927 |
10 |
81,70 |
83,20 |
85,40 |
250,30 |
83,433333 |
93,950579 |
11 |
78,10 |
78,80 |
81,30 |
238,20 |
79,400000 |
89,408821 |
12 |
88,30 |
89,00 |
92,20 |
269,50 |
89,833333 |
101,157335 |
Σ |
1058,00 |
1066,00 |
1073,00 |
3197,00 |
1065,666667 |
1200,000000 |
У середньому за рік |
88,17 |
88,83 |
89,42 |
= 88,805556 |
= 88,805556 |
|
В графі 1 розрахункової таблиці місяці кожного року пронумеруємо від 1 до 12 й відповідно до кожного з них у наступних графах представимо помісячно таку інформацію: в графи 2-4 перенесемо початкові дані про товарооборот; в графі 5 обчислимо за наведеною формулою сумарні значення товарообороту за три роки; в графі 6 – середні значення товарообороту за три роки; в графі 7 – значення середніх індексів сезонності (в процентах), як співвідношення відповідних даних графи 6 і середнього рівня ряду з підсумкової комірки останньої. У підсумковій комірці графи 7 виконаємо перевірку щодо виконання тотожності: середнє арифметичне середніх індексів сезонності повинно дорівнювати 100 % (виконується).
Побудуємо сезонну хвилю (рис. 2 і рис.3 нижче).
Висновок: У даному ряду кожного року відбуваються сезонні коливання місячних значень середньоденного товарообороту галузі порівняно з його середньорічним значенням: з січня по квітень включно він залишається у середньому нижчим за середньорічне значення, але «відставання» поступово скорочується з 5,67 % (94,33 – 100) до 0,41 % (99,59 – 100); в травні – різко зменшується та «відстає» від середнього на 10,03 % (89,97 – 100); в червні –
різко збільшується та «випереджає» середнє на 26,23 % (126,23 – 100); протягом липня ця тенденція зберігається, але на трошки нижчому рівні 116,06 % (116,06 – 100); з серпня по листопад включно товарооборот знов є нижчим за середньорічне його значення відповідно на 4,70 % (95,30 – 100), 0,34 % (99,66 – 100), 6,05 % (93,95 – 100), 10,59 % (89,41 – 100); і лише к завершенню року він на 1,16 % (101,16 – 100) «випереджає» середнє.
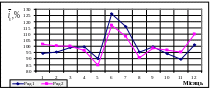

Рис. 2. Модель сезонної хвилі (лінійна діаграма) щомісячного середньоденного
товарообороту галузі протягом умовного року, побудована: ряд 1 –
 методом
постійного середнього, ряд 2 – методом
змінного середнього
методом
постійного середнього, ряд 2 – методом
змінного середнього
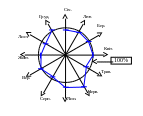
Рис. 3. Модель сезонної хвилі
(радіальна діаграма)
щомісячного середньо-
денного товарообороту
галузі протягом умовного
року, побудована методом
постійного середнього
Застосування
методу постійного середнього в умовах
даної задачі є виправданим, тому що
інтенсивність змін середньорічних
значень товарообороту є майже непомітною:
середньорічний темп приросту становить
0,17 % (по результатах розрахунків в
нижньому рядку розрахункової таблиці
маємо:
![]() ≈
100,71 (%),
≈
100,71 (%),
![]() =
100,71 – 100 = 0,71 (%)).
=
100,71 – 100 = 0,71 (%)).
Метод рядів Фур’є.
Задача №28. Завдання. За умов задачі №27 побудувати математичну модель внутрішньорічної динаміки середньоденного товарообороту галузі, скориставшись методом рядів Фур’є, а потім методом змінного середнього – сезонну хвилю (результати подати таблицею та графічно на рис. 1 і 2 в задачі №27). Зробити висновки.
Розв’язок. Дана задача зводиться до визначення теоретичних значень рівня ряду динаміки по перших гармоніках ряду Фур’є та їх подальшого використання у визначенні середнього індексу сезонності методом змінного середнього.
1) Побудуємо модель внутрішньорічної динаміки.
Для зручності результати проміжних розрахунків зведемо в розрахункову таблицю №1.
Розрахункова таблиця №1
i |
ti = і × × π/6 |
yi |
costi |
sinti |
yi ∙ costi |
yi ∙ sinti |
yti |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
π/6 |
83,40 |
1,000000 |
0,000000 |
83,400000 |
0,000000 |
82,30051726 |
2 |
2π/6 |
84,30 |
0,866025 |
0,500000 |
73,005942 |
42,150000 |
84,51027144 |
3 |
3π/6 |
85,90 |
0,500000 |
0,866025 |
42,950000 |
74,391582 |
87,87094353 |
4 |
4π/6 |
86,10 |
0,000000 |
1,000000 |
0,000000 |
86,100000 |
91,48204416 |
5 |
5π/6 |
79,30 |
-0,500000 |
0,866025 |
-39,650000 |
68,675815 |
94,37598183 |
6 |
6π/6 |
107,90 |
-0,866025 |
0,500000 |
-93,444141 |
53,950000 |
95,77732828 |
7 |
7π/6 |
106,00 |
-1,000000 |
0,000000 |
-106,000000 |
0,000000 |
95,31059385 |
8 |
8π/6 |
86,30 |
-0,866025 |
-0,500000 |
-74,737992 |
-43,150000 |
93,10083967 |
9 |
9π/6 |
90,70 |
-0,500000 |
-0,866025 |
-45,350000 |
-78,548504 |
89,74016758 |
10 |
10π/6 |
81,70 |
0,000000 |
-1,000000 |
0,000000 |
-81,700000 |
86,12906695 |
11 |
11π/6 |
78,10 |
0,500000 |
-0,866025 |
39,050000 |
-67,636584 |
83,23512928 |
12 |
12π/6 |
88,30 |
0,866025 |
-0,500000 |
76,470043 |
-44,150000 |
81,83378283 |
13 |
13π/6 |
87,80 |
1,000000 |
0,000000 |
87,800000 |
0,000000 |
82,30051726 |
14 |
14π/6 |
88,40 |
0,866025 |
0,500000 |
76,556646 |
44,200000 |
84,51027144 |
15 |
15π/6 |
88,50 |
0,500000 |
0,866025 |
44,250000 |
76,643248 |
87,87094353 |
16 |
16π/6 |
90,40 |
0,000000 |
1,000000 |
0,000000 |
90,400000 |
91,48204416 |
17 |
17π/6 |
78,20 |
-0,500000 |
0,866025 |
-39,100000 |
67,723187 |
94,37598183 |
18 |
18π/6 |
113,40 |
-0,866025 |
0,500000 |
-98,207281 |
56,700000 |
95,77732828 |
19 |
19π/6 |
97,40 |
-1,000000 |
0,000000 |
-97,400000 |
0,000000 |
95,31059385 |
20 |
20π/6 |
80,00 |
-0,866025 |
-0,500000 |
-69,282032 |
-40,000000 |
93,10083967 |
21 |
21π/6 |
90,90 |
-0,500000 |
-0,866025 |
-45,450000 |
-78,721709 |
89,74016758 |
22 |
22π/6 |
83,20 |
0,000000 |
-1,000000 |
0,000000 |
-83,200000 |
86,12906695 |
23 |
23π/6 |
78,80 |
0,500000 |
-0,866025 |
39,400000 |
-68,242802 |
83,23512928 |
24 |
24π/6 |
89,00 |
0,866025 |
-0,500000 |
77,076261 |
-44,500000 |
81,83378283 |
25 |
25π/6 |
80,10 |
1,000000 |
0,000000 |
80,100000 |
0,000000 |
82,30051726 |
26 |
26π/6 |
81,50 |
0,866025 |
0,500000 |
70,581070 |
40,750000 |
84,51027144 |
27 |
27π/6 |
89,40 |
0,500000 |
0,866025 |
44,700000 |
77,422671 |
87,87094353 |
28 |
28π/6 |
88,60 |
0,000000 |
1,000000 |
0,000000 |
88,600000 |
91,48204416 |
29 |
29π/6 |
82,20 |
-0,500000 |
0,866025 |
-41,100000 |
71,187288 |
94,37598183 |
30 |
30π/6 |
115,00 |
-0,866025 |
0,500000 |
-99,592921 |
57,500000 |
95,77732828 |
31 |
31π/6 |
105,80 |
-1,000000 |
0,000000 |
-105,800000 |
0,000000 |
95,31059385 |
32 |
32π/6 |
87,60 |
-0,866025 |
-0,500000 |
-75,863825 |
-43,800000 |
93,10083967 |
33 |
33π/6 |
83,90 |
-0,500000 |
-0,866025 |
-41,950000 |
-72,659531 |
89,74016758 |
34 |
34π/6 |
85,40 |
0,000000 |
-1,000000 |
0,000000 |
-85,400000 |
86,12906695 |
35 |
35π/6 |
81,30 |
0,500000 |
-0,866025 |
40,650000 |
-70,407865 |
83,23512928 |
36 |
36π/6 |
92,20 |
0,866025 |
-0,500000 |
79,847542 |
-46,100000 |
81,83378283 |
Σ |
x |
3197,00 |
0,000000 |
0,000000 |
-117,090689 |
48,176795 |
3197,000000 |
Нумерацію місяців трьох послідовних років представимо наскрізною від 1 до 36 (графа 1), час ti – таким (значення в графі 2), що набуває значень, кратних π/6 (1/12-ій року як 1/12-ій одного обороту повного кола). Розкладення функції Yt на ортогональні складові sin і cos стає можливим через визначення відповідних значень sinti (значення в графі 5) costi (значення в графі 4) і множенням їх на фактичні значення yi (значення в графі 3) рівня ряду.
Отже, коефіцієнти Фур’є становлять (7.41, 7.42):
а0 = 3197 : 36 ≈ 88,805556 (тис.грош.од.);
а1 = 2 ∙ (-117,090689) : 36 ≈ -6,505038 (тис.грош.од.);
b1 = 2 ∙ (48,176795) : 36 ≈ 2,676489 (тис.грош.од.).
Остаточно, ряд Фур’є має вид (7.40):
Yt = 88,805556 – 6,505038 ∙ cost + 2,676489 ∙ sint.
Їх підстановка в остаточне рівняння теоретичної моделі дає такі результати (значення в графі 8):
ytсіч. = 88,805556 – 6,505038 ∙ 1,0 + 2,676489 ∙ 0,0 ≈ 82,30051726 (тис.грош.од.);
ytлют. = 88,805556 – 6,505038 ∙ 0,866025 + 2,676489 ∙ 0,5 ≈
≈ 82,30051726 (тис.грош.од.);
…
ytгруд. = 88,805556 – 6,505038 ∙ 0,866025 + 2,676489 ∙ (-0,5) ≈
≈ 82,30051726 (тис.грош.од.).
Сума фактичних і теоретичних значень рівня ряду має бути однаковою: дійсно 3197 = 3197. Враховуючи періодичність функцій sin і cos, у другому і третьому році Yt набуває таких же самих значень.
Побудуємо теоретичний ряд динаміки (ряд 2 на рис. 1 в задачі №27).
2) Визначимо значення середнього індексу сезонності аналогічно задачі №24, але в якості теоретичних рівнів візьмемо значення, отримані в попередньому пункті задачі методом рядів Фур’є.
Для зручності результати проміжних розрахунків зведемо в розрахункову таблицю №2.
Розрахункова таблиця №2
i |
yij |
|
|
yti (по першій гармоніці) |
|
yti (по першій-третій гармоніках) |
||
j = 1 |
j = 2 |
j = 3 |
||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
83,40 |
87,80 |
80,10 |
251,30 |
83,766667 |
82,300517 |
101,78146 |
84,731073 |
2 |
84,30 |
88,40 |
81,50 |
254,20 |
84,733333 |
84,510271 |
100,26395 |
88,221383 |
3 |
85,90 |
88,50 |
89,40 |
263,80 |
87,933333 |
87,870944 |
100,07100 |
86,245944 |
4 |
86,10 |
90,40 |
88,60 |
265,10 |
88,366667 |
91,482044 |
96,594548 |
83,107044 |
5 |
79,30 |
78,20 |
82,20 |
239,70 |
79,900000 |
94,375982 |
84,661370 |
90,531537 |
6 |
107,90 |
113,40 |
115,00 |
336,30 |
112,100000 |
95,777328 |
117,04231 |
103,346773 |
Продовження розрахункової таблиця №2
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
7 |
106,00 |
97,40 |
105,80 |
309,20 |
103,066667 |
95,310594 |
108,13768 |
103,818927 |
8 |
86,30 |
80,00 |
87,60 |
253,90 |
84,633333 |
93,100840 |
90,905016 |
91,000840 |
9 |
90,70 |
90,90 |
83,90 |
265,50 |
88,500000 |
89,740168 |
98,618046 |
82,037390 |
10 |
81,70 |
83,20 |
85,40 |
250,30 |
83,433333 |
86,1290675 |
96,870123 |
83,565178 |
11 |
78,10 |
78,80 |
81,30 |
238,20 |
79,400000 |
83,235129 |
95,392415 |
85,468463 |
12 |
88,30 |
89,00 |
92,20 |
269,50 |
89,833333 |
81,833783 |
109,77536 |
83,592116 |
Σ |
88,17 |
88,83 |
89,42 |
3197,00 |
х |
1065,666667 |
Середнє = 100,00944 |
1065,666667 |
В графи 2-4 перенесемо фактичні значення рівня ряду динаміки, в графу 7 – теоретичні значення з графи 8 розрахункової таблиці №1; в графі 5 обчислимо за наведеною формулою сумарні значення товарообороту за три роки, в графі 6 – середні значення товарообороту за три роки, в графі 8 – значення середніх індексів сезонності (в процентах) як співвідношення відповідних даних графи 6 і графи 7. У підсумковій комірці графи 8 виконаємо перевірку щодо виконання тотожності: середнє арифметичне середніх індексів сезонності повинно дорівнювати 100 % (виконується; незначна відмінність від 0 у третьому і т.д. розрядах пояснюється округленням результатів проміжних розрахунків).
Побудуємо сезонну хвилю (ряд 2 на рис. 2 в задачі №27).
Висновки:
1) Теоретично внутрішньорічну динаміку щомісячного середньоденного товарообороту галузі, який змінюється від мінімального його значення 78,10 тис.грош.од. в листопаді 1-го року до максимального його значення 115 тис.грош.од. в червні 3-го року, можна представити рядом Фур’є – гармонічною функцією Yt = 88,805556 – 6,505038 ∙ cost + 2,676489 ∙ sint з ортогональними складовими sin і cos, яка осереднює сезонні коливання ряду динаміки в межах від 81,83378 тис.грош.од. в грудні умовного року до 95,77733 тис.грош.од. в червні умовного року з амплітудою в 6,97177 тис.грош.од. коливань відносно середнього його значення а0 = 88,80556 тис.грош.од. (88,80556 – 81,83378 = 95,77733 – 88,80556 = 6,97177). Максимальна відмінність теоретичних і фактичних значень сягає 20,69 % (в травні 2-го року: (94,375982 – 78,20) : 78,20 ∙ 100 ≈ 20,69). Вирівнювання ряду динаміки додатково гармоніками вищого (другого і третього) порядку (в графі 9 розрахункової таблиці №2 представлені значення функції Yt = 88,805556 – 6,505038 × × cost + 2,676489 ∙ sint + 5,469444 ∙ cos2t – 2,227610 ∙ sin2t – 3,038889 ∙ cos3t + + 2,905556 ∙ sin3t (із-за великого обсягу розрахунків проміжні результати не наводяться), графік якої, як ряд 3, зображений на рис. 1 в задачі №27) зменшує відмінність до 15,77 % ((90,531537 – 78,20) : 78,20 ∙ 100 ≈ 15,77).
2) Сезонна хвиля, побудована через аналітичне вирівнювання ряду динаміки методом рядів Фур’є, нагадує хвилю, отриману в задачі №27. Принципова відмінність двох хвиль спостерігається лише в січні-квітні умовного року, коли середній індекс сезонності не збільшується, як раніше (загальне чотиримісячне збільшення становило 5,18 %), а, навпаки, зменшується зі 101,78 % до 96,59 % (на ті ж самі 5,18 %). У подальшому тенденція його зміни зберігаєть-
ся, але із відмінністю в значеннях індексу не більше 8,52 % в грудні умовного року ((109,77536 – 101,157335) : 101,157335 ∙ 100 ≈ 8,52).


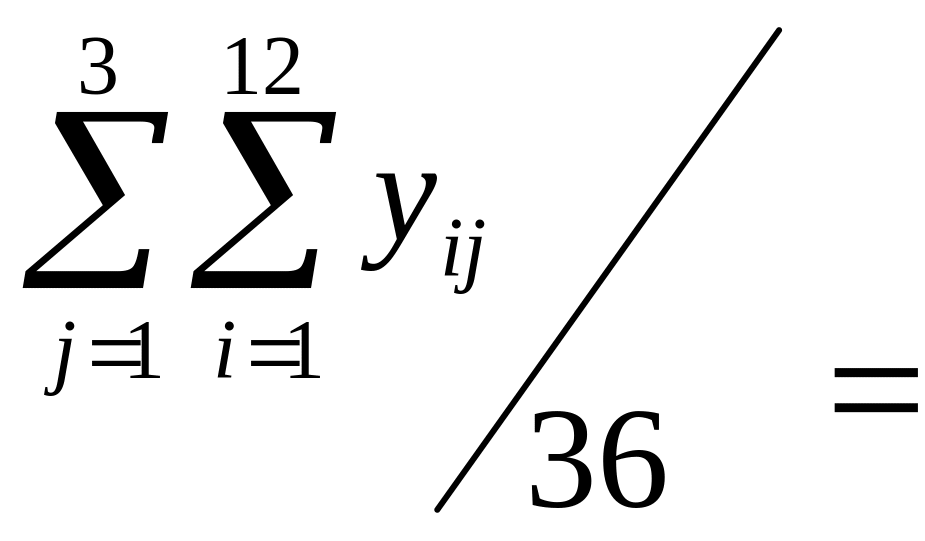
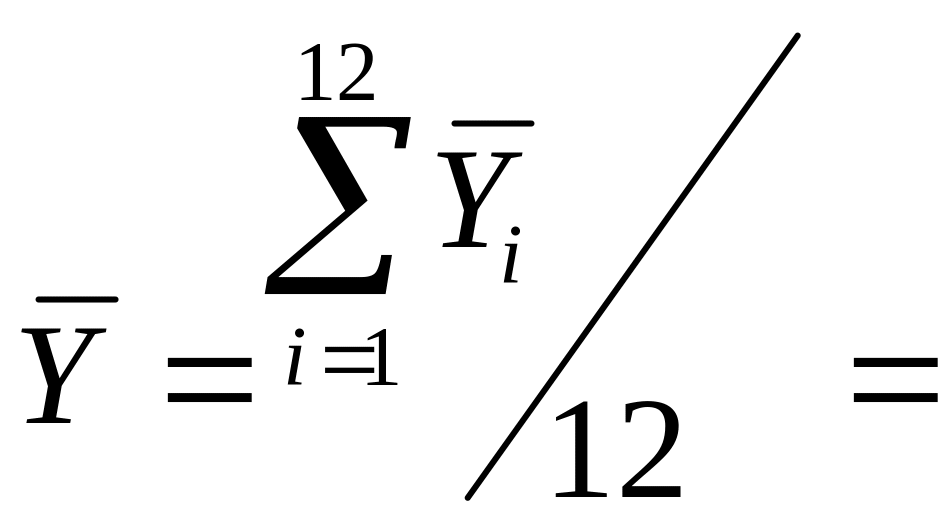
 =
100,000000
=
100,000000