Лекционный материал (математическое моделирование)
Лекция №1.
1. Основные предположения о гравитационном режиме течения грунтовых вод
Пористая среда представляет собой пласт водопроницаемого материала (песок, глина), ограниченного снизу грунтом, не пропускающим воду (гранит), а сверху – поверхностью земли (рис. 2.1).
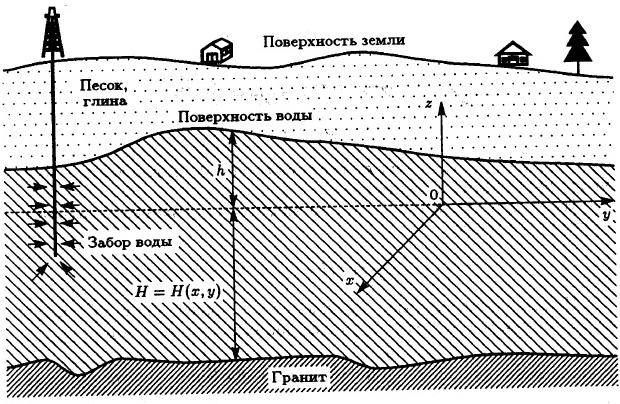
Рис. 1.1
Если из-за интенсивной работы артезианских скважин или в результате обильных осадков уровень воды в каком-либо месте слоя изменяется, то под действием силы тяжести начинается движение жидкости, выравнивающее ее свободную поверхность.
Для описания этого процесса, введем ряд предположений:
1)
вода рассматривается как несжимаемая
жидкость с постоянной плотностью
;
2) толщина пласта много меньше его ширины и длины;
3)
подстилающая поверхность не имеет
разрывов и изломов, задающая ее известная
функция
-
достаточно гладкая функция своих
аргументов;
4)
свободная поверхность воды
плавно меняется с изменением координат
;
5) грунтовые воды нигде не выходят на поверхность земли, причем на свободной поверхности жидкости давление постоянно;
6)
грунт однороден, т.е. его физико-механические
свойства не зависят от
.
Первое
предположение вполне естественно,
поскольку в рассматриваемом процессе
не могут достигаться давления, способные
заметно изменить плотность воды.
Остальные предположения упрощающие.
Например, второе предположение (тонкий
пласт) означает, что течение жидкости
двумерное и все его характеристики не
зависят от координаты
,
последние два предположения позволяют
построить модель, единообразную во всех
точках грунта и т.д. Вместе с тем,
предположения 1) – 6) не выхолащивают
сути процесса, так как они выполняются
в большом количестве реальных ситуаций.
2. Баланс массы в элементе грунта.
Выделим
в пласте элементарный объем, образующийся
в результате пересечения вертикальной
призмы
подстилающей
и свободной поверхностями грунта.
Поскольку размеры призмы
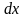и
малы,
а функции
и
гладкие
(предположения 3), 4)), то получившееся
тело с хорошей степенью точности можно
считать параллелепипедом. Ведем
неизвестные функции
и
-
составляющие скорости жидкости вдоль
осей
(рис. 1.2).
Подсчитаем
количество жидкости, входящей в
параллелепипед и выходящей из него за
промежуток времени
.
Через
грань
в
элементе грунта входит масса воды,
равная объему прошедшей через нее
жидкости, умноженному на плотность
,
т.е. величина
,
а
через грань
выходит
массы воды
.
Рис. 1.2
В
этом выражении в сравнении с предыдущем
добавляется член, описывающий приращение
функции
при
переходе от плоскости
к
плоскости
.
Сама же величина
имеет
смысл потока массы (вещества).
Итак, при движении жидкости вдоль оси , в элементе грунта накапливается масса
.
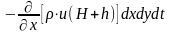Проведя
аналогичные рассуждения
и
,
получаем изменение массы воды вдоль за
счет ее движения вдоль оси
:
.
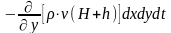Поскольку вдоль оси в элементе грунта жидкость не втекает и не вытекает из него (снизу – пласт подстилающий, а через свободную поверхность нет потока вещества), то суммарное изменение массы воды в элементе грунта равно
. (1)
Общее
количество жидкости в параллелепипеде
равно его объему, умноженному на плотность
и
на коэффициент пористости
(так как часть объема занята грунтом):
.
Изменение массы воды в элементе за время , очевидно, равно
.
Учитывая,
что
,
,
из последнего выражение получаем
, (2)
и, приравнивая (1) и (2), приходим к уравнению неразрывности, выражающему закон сохранения массы в рассматриваемом процессе:
. (3)
В уравнении (3) скорость изменения рассматриваемой величины (в данном случае массы) со временем определяется дивергенцией потока этой величины – свойство, характерное для многих моделей, получаемых из законов сохранения.
С
учетом того, что
,
,
уравнение (3) переписывается в более
простой форме:
. (4)