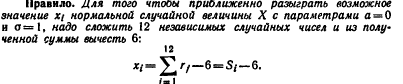14. Оценка генеральной дисперсии по выборочной средней.

Пусть из генеральной совокупности в рез-те n незав-ых наблюдений над количественным признаком Х извлечена повторная выборка объема n. При этом . Требуется оценить неизв.генер.дисперсию. Мат.ожидание выборочной дисперсии равно

и не равно оцениваемой генер.дисперсии. И в итоге в качестве оценки генер.дисперсии принимают исправленную дисперсию

15.Точечная оценка, доверительный интервал для точечной оценки. Уровень значимости оценки и его влияние на доверительный интервал.

Точечной наз. оценку, которая опр. одним числом. Интервальной наз.оценку, которая опр. 2мя числами – концами интервала. Интервальные оценки позволяют установаить точность и надежность оценок.

16.Доверительные интервалы для оценки математического ожидания нормального распределения при известном и неизвестном σ.

Доверительный интервал для оценки математического ожидания при известном s.

Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение этого распределения -s. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью g. Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением s.

Потребуем, чтобы выполнялось равенство

Заменив Х и s, получим  

получим

Доверительный интервал для оценки математического ожидания при неизвестном s.

В качестве неизвестного параметра s используют исправленную дисперсию s² . Заменяя s на s, t на величину t_g. Значение этой величины зависит от надежности g и объема выборки n и определяется по " Таблице значений t_g." 

и доверительный интервал имеет вид

17.Нулевая и конкурирующая гипотеза. Виды конкурирующих гипотез. Критическая область. Односторонняя и двусторонняя критические области. Мощность критерия.

Выдвигается основная (нулевая) гипотеза Н₀ и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу Н₁, которая противоречит нулевой. Под критической областью понимают совокупность значений критерия, при которых нулевую гипотезу Н₀ отвергают. Критическую область при заданном уровне значимости следует строить так, чтобы мощность критерия была максимальной. В результате статистической проверки гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; вероятность совершить такую ошибку обозначают α и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают β, а мощностью критерия является вероятность 1-β.

18. Сравнение двух дисперсий нормальных генеральных совокупностей.

20.Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (независимые выборки).

22.Сравнение двух средних произвольно распределенных генеральных совокупностей (большие независимые выборки).

23.Cравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки).

24.Критерий согласия Пирсона. Проверка гипотезы о нормальном распределении генеральной совокупности.

25.Проверка гипотезы о нормальном распределении генеральной совокупности с помощью критерия согласия Колмогорова.

Критерии Колмогорова и Смирнова прим. в непр.функции распределения

В случаях критерий Пирсона мера расх. между теор.и практ.частотами явл. функция 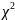. В случаях критерий Колмогорова и Смирнова выбор меры расхождения связан с эмперической функцией распределения вида D_n=max(F_i-F_oi), где F_i=n_i/n.

А для критерия Смирнова

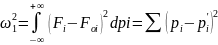
Эти функции могут быть легко вычислены по выборке, не треб.собрать какие-либо интегралы, все сводится к обычному суммированию по теореме Левенко при вып.гипотезы: число Д_n(расх)→0 при n →∞

Оказывается, если Д_n домножить на 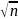, то в пределе получится нетривиальное распределение, называемое распределение Колмогорова. Более точно, верна теорема  Колмогорова : Если гипотеза  H₀ верна и F₀(t) непрерывна, то

1.распределение статистики является одним и тем же для любой функции распределения F₀(t) и

2.у последовательности существует предельное распределение при .

Аналогичное по характеру утверждение имеет место и для статистики Смирнова, а именно, при верной гипотезе H₀ и непрерывной F₀(t)

распределение зависит только от n и не зависит от F₀(t),

у последовательности существует предельное распределение при .

Теоремы  Колмогорова  и Смирнова являются основой для построения соответствующих  критериев   согласия  с критическими множествами вида     и

соответственно. Числа C_1,C₂ определяются по заданным уровням значимости из таблиц допредельных (или предельных, если n очень велико) распределений  Колмогорова  и Смирнова.

26.Определение теоретических частот для проверки нормальности распределения с помощью критерия Пирсона.

28.Разыгрывание дискретной случайной величины. Разыгрывание противоположных событий.

29.Разыгрывание непрерывной случайной величины. Метод обратных функций.

30.Приближенное разыгрывание нормальной случайной величины.