Лабораторная работа 1 Изучение временных характеристик типовых динамических звеньев

Цель работы: - изучить дифференциальные уравнения и передаточные функции,

описывающие типовые динамические звенья;

- исследовать графики переходных характеристик типовых

динамических звеньев.

Задание 1. Получить графики переходных характеристик следующих типовых звеньев

при двух видах входных воздействий:

1) Усилительное (пропорциональное) звено

Передаточная функция: W(p) = k , k =

2) Интегрирующее (астатическое) звено

Передаточная функция: W(p) = k/p , k = 1/T_и =

3) Инерционное (апериодическое) звено I-го порядка

Передаточная функция: W(p) = k/(Tp+1) , k = , T =

4) Звено чистого запаздывания

Передаточная функция: W(p) = e^{- p} , =

5) Колебательное звено

Передаточная функция: W(p) = k/(T²p² + 2 Tp + 1) , k = , T = , =

Виды входных воздействий:

а) Единичное ступенчатое воздействие б) Импульсное воздействие

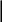
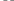1

t= t₁= t₂=

Задание 2. Исследовать устойчивое колебательное звено, подавая на его вход

единичное ступенчатое воздействие и варьируя значения следующих параметров

его передаточной функции:

- коэффициента передачи k в диапазоне 0.5 - 2.5 (при исходных значениях T и );

- постоянной времени T в диапазоне 5 - 25 с (при исходных значениях k и );

- коэффициента затухания в диапазоне 0.1 - 0.9 (при исходных значениях k и T ).

Примечание: каждый из параметров достаточно проварьировать 3 раза.

Определить зависимость максимального отклонения X_max и длительности переходного процесса t_пп , как функций от параметров k , T и .

Результаты исследований представить в виде графиков.

Сделать выводы по работе:

- описать и объяснить реакцию типовых динамических звеньев на каждое из входных

воздействий, исходя из их дифференциальных уравнений и передаточных функций;

- проанализировать, как влияют изменения значений k, T и на форму, максимальное

отклонение и длительность переходного процесса в колебательном звене.

Лабораторная работа 2 Исследование замкнутой автоматической системы регулирования

Цель работы: - изучить свойства объекта регулирования;

- исследовать влияние законов регулирования и параметров настройки

регуляторов на прямые показатели качества работы АСР.

Задание:

Объект регулирования представлен в виде последовательного соединения двух инерци-онных звеньев I-го порядка (1 и 2) и звена чистого запаздывания (3). Передаточные функции звеньев: W₁(p)= k₁/(T₁p+1) , k₁ = , T₁ =

W₂(p)= k₂/(T₂p+1) , k₂ = , T₂ =

W₃(p)= e^{- p} , =

В схемах АСР в качестве регуляторов используются:

- пропорциональный регулятор (П-регулятор) с передаточной функцией W_п(p) = k_п ;

- изодромный регулятор (ПИ-регулятор) с передаточной функцией W_пи(p) = k_пи(T_изp+1)/T_изp

Исследования АСР проводить при подаче единичного ступенчатого воздействия (t = 2) и импульсного воздействия (t₁ = 5, t₂ = 15).

Порядок выполнения работы:

1. Получить кривые переходного процесса для выходной величины объекта регулирования x(t) (рисунок 1), подавая по очереди на его вход единичное ступенчатое и импульсное воз-

д ействия. 1 2 3

f(t) x(t)

W₁(p) W₂(p) W₃(p)

Рисунок 1 – Структурная схема объекта регулирования

По графику переходной характеристики определить параметры передаточной функции объекта: коэффициент передачи k_об , постоянную времени T_об и время запаздывания _об .

По графику импульсной характеристики определить максимальное отклонение выходной величины X_max и время t_р окончательного вхождения величины x(t) в область, заданную вокруг ее установившегося значения, т.е. в зону _ , где составляет 5% от задания.

Оценить свойства объекта регулирования.

2. Исследовать работу одноконтурной АСР (рисунок 2) с П-регулятором при отработке единичного ступенчатого воздействия по заданию y(t) (при этом f(t) = 0), изменяя параметр настройки регулятора k_п в диапазоне 0.5 - 2.

Определить зависимость величины статической ошибки регулирования (как разницы между фактически установившимся значением выходной величины x(t) и тем ее значением, которое должно было бы установиться) от изменения k_п. Найти критическое значение k_п^кр, соответствующее границе устойчивости системы.

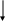f(t)

объект

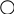y(t) (t) (t) z(t) x(t)

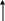
W_рег(p) W₁(p) W₂(p) W₃(p)

-

Рисунок 2 – Структурная схема одноконтурной АСР

3. Получить график переходного процесса в одноконтурной АСР (рисунок 2) с ПИ-регулято-ром (при любом одном значении k_пи из диапазона 0.5 - 2 и T_из из диапазона 10 - 60 с) при отработке единичного ступенчатого воздействия по заданию y(t) (при этом f(t) = 0). Убедиться в отсутствии статической ошибки.

4. Исследовать работу одноконтурной АСР (рисунок 2) с П-регулятором при отработке импульсного воздействия по возмущению f(t) (при этом y(t) = 0), изменяя параметр настройки k_п в диапазоне 0.5 - 2.

Построить графики зависимости X_max и t_р от изменения k_п. Определить оптимальное зна-чение k_п^опт, соответствующее минимальному времени переходного процесса t_р.

5. Исследовать работу одноконтурной АСР (рисунок 2) с ПИ-регулятором при отработке импульсного воздействия по возмущению f(t), изменяя параметры настройки регулятора k_пи в диапазоне 0.5 - 2 (при этом T_из=const) и T_из в диапазоне 10 - 60 с (при этом k_пи=const).

Построить графики зависимости X_max и t_р от изменения k_пи и T_из. Определить оптимальные значения k_пи^опт и T_из^опт, соответствующие минимальному времени переходного процесса t_р.

6. В отчете о работе представить:

- графики кривых разгона объекта регулирования, полученные при двух типах внешних воздействий (пункт 1);

- график зависимости величины статической ошибки регулирования от изменения k_п

( = F(k_п) ) и графики переходных процессов в АСР с П-регулятором, иллюстрирующие изменение статической ошибки регулирования (пункт 2);

- график переходного процесса в одноконтурной АСР с ПИ-регулятором (пункт 3);

- таблицы, иллюстрирующие поиск оптимальных настроек П- и ПИ-регуляторов (пункты 4 и 5), и построенные по их данным графики зависимостей характеристик переходных процессов (t_р, X_max) от варьируемых параметров настройки регуляторов ;

- графики переходных процессов, соответствующих оптимальным значениям настроечных параметров П- и ПИ-регуляторов.

Сделать подробные выводы по каждому пункту работы.

Завершить выводы выбором АСР, обеспечивающей наибольшее быстродействие.

ЛАБОРАТОРНАЯ РАБОТА 3

Устойчивость автоматических систем регулирования

Цель работы: освоение техники выделения областей устойчивости в пространстве

параметров настройки регулятора и оценка качества переходных

процессов, полученных при определенных комбинациях значений

настроечных параметров.

Задание: дана структурная схема линейной АСР k_об

y(t) (t) (t) x(t) W_об(p) =

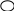
W_рег(p) W_об(p) (T₁p+1)(T₂p+1)

k_об = , T₁ = , T₂ =

k_рег

W_рег(p) = , где T_б - постоянная времени балластной инерционности

T_бp+1 реального П-регулятора.

k_рег = , T_б =

Порядок выполнения работы:

1. Построить кривые D-разбиения в плоскости изменения значения коэффициента K, в плос-

кости изменения значения T_б , в плоскости изменения значений K и T_б одновременно.

2. Рассчитать корни характеристического уравнения замкнутой системы и построить корне-

вые годографы для ряда точек, указанных преподавателем на плоскостях кривых D-раз-

биения, при изменении: а) значения K ; б) значения T_б ; в) значений K и T_б одновременно.

3. Построить графики амплитудно-фазовых частотных характеристик (АФЧХ) разомкнутой

системы для всех исследуемых точек.

4. В инструментальной среде VisSim получить графики переходных процессов для всех

исследуемых точек.

Отчет о работе должен содержать:

- вывод характеристического уравнения замкнутой системы;

- графическое выделение областей, претендующих на устойчивость, для каждой из постро-

енных кривых D-разбиения;

- проверку выделенных областей на устойчивость, используя для этой цели коэффициенты

характеристического уравнения замкнутой системы (методика приведена в учебнике “Тео-

рия автоматического управления”/Под ред. А.А.Воронова, глава “Устойчивость линейных

САУ”, § “Построение областей устойчивости в плоскости параметров системы”, пример);

- допустимые диапазоны изменения настроечных параметров П-регулятора (K и T_б), в преде-

лах которых система устойчива (с учетом некоторого запаса устойчивости);

- анализ влияния изменяемых параметров настройки (K и T_б) П-регулятора (или коэффици-

ентов характеристического уравнения) на корни характеристического уравнения замкнутой

системы;

- оценку запаса устойчивости системы по корневым годографам;

- определение величины запаса устойчивости по модулю и по аргументу для всех исследуе-

мых точек с помощью критерия Найквиста;

- анализ влияния изменяемых параметров K и T_б на АФЧХ разомкнутой системы;