
- •Цепь переменного тока при последовательном соединении элементов
- •Цепь переменного тока при параллельном соединении элементов
- •Трехфазное соединение звездой с нейтральным проводом
- •Пример расчета трехфазной нагрузки, соединенной звездой с нейтральным проводом
- •Трансформаторы
- •Работа трансформатора под нагрузкой
- •Внешняя характеристика трансформатора
- •Механические характеристики эд и им
- •Устройство и принцип действия ад.
- •Основные уравнения ад
- •Момент вращения ад
- •Механическая характеристика ад
- •Регулирование скорости вращения ад
- •Способы пуска ад
- •2. Методы, основанные на сопротивления ротора r2
- •Устройство и принцип действия дпт.
- •Классификация дпт по способу возбуждения.
- •Принцип действия дпт.
Цепь переменного тока при последовательном соединении элементов
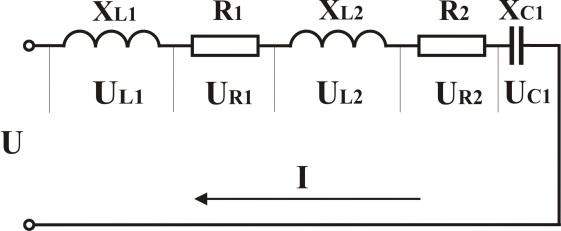
i=Imsinωt
При последовательном соединении
элементов ток на всех участках цепи
одинаков. Действующее значение тока
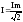 и угловую частоту ω можно найти, используя
закон изменения токаi=Imsinωt
и угловую частоту ω можно найти, используя
закон изменения токаi=Imsinωt
Падение напряжения на каждом элементе цепи можно определить из закона Ома
UR
= I R ; UL
= I XL
= I 2π f L = I ωL; UC
= I XC
=
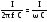
Приложенное напряжение Uравно геометрической сумме падений напряжения на каждом элементе последовательной цепи (IIзакона Кирхгофа).
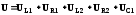 – сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД)
– сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД)
Порядок построения ВД:
Строим вектор тока
Относительно вектора тока строим вектор падения напряжения на первом элементе цепи, учитывая величину и направление угла сдвига фаз между током и напряжением.
Из конца этого вектора аналогично строим вектор падения напряжения на следующем элементе цепи и т.д. – в результате получим векторную сумму падений напряжения на всех элементах цепи, т.е. приложенное напряжение
 .
.

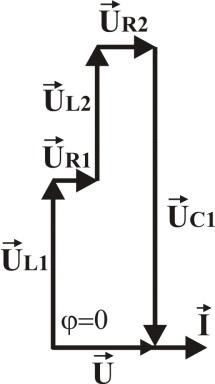
ВД при резонансе напряжений
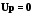
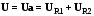
Численное значение приложенного напряжения Uможно определить из ВД
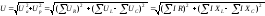
=

Где: 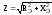 – полное сопротивление цепи
– полное сопротивление цепи
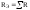 – эквивалентное активное сопротивление
цепи
– эквивалентное активное сопротивление
цепи
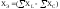 – эквивалентное реактивное
сопротивление цепи
– эквивалентное реактивное
сопротивление цепи
Резонанс в последовательной цепи (резонанс напряжений)
При резонансе напряжений сумма индуктивных напряжений равна сумме емкостных, следовательно, эквивалентное реактивное напряжение
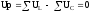 – условие резонанса напряжений
– условие резонанса напряжений
Следовательно, при резонансе напряжений
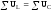

Приложенное напряжение
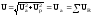 – равно активному.
– равно активному.
Полное сопротивление цепи
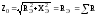 –
равно сумме активных сопротивлений и
минимально, т.е. всю цепь можно заменить
эквивалентным активным сопротивлениемRЭ.
–
равно сумме активных сопротивлений и
минимально, т.е. всю цепь можно заменить
эквивалентным активным сопротивлениемRЭ.
Ток в цепи
 – максимален, и падение напряжения на
отдельных реактивных элементах может
быть больше приложенного напряжения
(см. ВД при резонансе).
– максимален, и падение напряжения на
отдельных реактивных элементах может
быть больше приложенного напряжения
(см. ВД при резонансе).
При резонансе напряжений приложенное напряжение совпадает по фазе с током (φ = 0), т.е. несмотря на наличие реактивных элементов, цепь ведет себя как чисто активный приемник.
Цепь переменного тока при параллельном соединении элементов

При параллельном соединении элементов напряжение на каждой ветви схемы одинаково и равно приложенному. Каждая ветвь схемы представляет из себя последовательное соединение элементов, следовательно, можно для каждой из ветвей найти полное сопротивление Z, токIи угол сдвига фаз φ

Аналогично можно определить Z,Iи φ для остальных ветвей
По Iзакону Кирхгофа ток
в неразветвленной части цепи равен
геометрической сумме токов в ветвях –сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД).
–сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД).
Порядок построения ВД:
Строим вектор напряжения
Относительно вектора напряжения строим вектор тока первой ветви
 ,
учитываявеличину
и направление
угла сдвига фаз между током и напряжением
φ1.
,
учитываявеличину
и направление
угла сдвига фаз между током и напряжением
φ1.Из конца этого вектора строим вектор тока второй ветви и т.д. – в результате получим векторную сумму токов в ветвях, т.е. ток в неразветвленной части цепи.

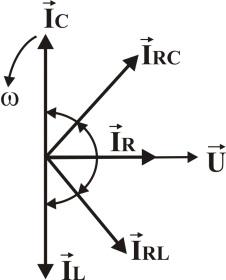
Численное значение полного тока Iможно определить из ВД, если разложить ток каждой ветви на две составляющие
Например, для первой ветви
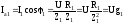 – активная составляющая токаI1
– активная составляющая токаI1
 – реактивная составляющая токаI1
– реактивная составляющая токаI1
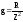 – активная проводимость отдельной
ветви
– активная проводимость отдельной
ветви
 – реактивная проводимость отдельной
ветви
– реактивная проводимость отдельной
ветви
Аналогично можно разложить на составляющие токи всех ветвей
Тогда из ВД, учитывая, что емкостные и индуктивные токи направлены в противоположные стороны, получим
 =
=
=
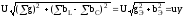
Где:  – активная составляющая полного тока
– активная составляющая полного тока
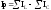 – реактивная составляющая полного
тока
– реактивная составляющая полного
тока
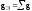 – эквивалентная активная проводимость
цепи
– эквивалентная активная проводимость
цепи
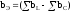 – эквивалентная реактивная проводимость
цепи
– эквивалентная реактивная проводимость
цепи
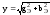 – полная проводимость цепи
– полная проводимость цепи
Резонанс в параллельной цепи (резонанс токов)
При резонансе токов сумма индуктивных токов равна сумме емкостных, следовательно, реактивная составляющая полного тока
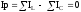 – условие резонанса токов
– условие резонанса токов
Следовательно, при резонансе токов
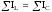
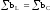
Полный ток (в неразветвленной части
цепи)
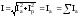 – равен активному, т.е. сумме активных
токов всех ветвей.
– равен активному, т.е. сумме активных
токов всех ветвей.
Полная проводимость цепи
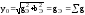 – равно сумме активных проводимостей
всех ветвей и минимальна.
– равно сумме активных проводимостей
всех ветвей и минимальна.
Ток в цепи
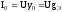 – минимален, т.е. параллельная цепь при
резонансе обладает минимальной
проводимостью, т.е. максимальным
сопротивлением.
– минимален, т.е. параллельная цепь при
резонансе обладает минимальной
проводимостью, т.е. максимальным
сопротивлением.
При резонансе токов полный ток совпадает по фазе с приложенным напряжением (φ = 0), т.е. вся цепь имеет чисто активный характер.
